Galileo Galilei y el Movimiento Uniformemente Acelerado (página 2)

V=V0 + at. (Para la caída
libre)

Galileo advertía que los incrementos de velocidad no
eran iguales para iguales distancias recorridas, lo cual se
demuestra aplicando la ecuación:

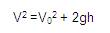
Como existe una dependencia lineal entre la velocidad y el
tiempo,
Sagredo, hombre culto
que forma parte de los tres personajes que dialogan entre
sí en la obra de Galileo, expuso a Salviati, personaje que
representaba a Galileo, lo siguiente: " como el tiempo es
subdivisible hasta el infinito, .. Al ir disminuyendo siempre en
tal razón, la velocidad que precede, no hay ningún
grado de velocidad tan pequeño,.. Para el que no haya
pasado el mismo móvil después de su partida desde
el reposo..". Es necesario decir que para Sagredo los instantes
de tiempo, cada vez más próximos al primero desde
su partida el movimiento es
tan tardío que no habría recorrido el
móvil.." Una milla en una hora, ni en un día, ni en
un año, ni en mil.." El sabio con su maestría
característica y persuadido en su yo interno del concepto de
infinitesimal, no conocido hasta entonces y aparecido con el
cálculo
diferencial, posterior a Galileo, replico: "dices parecerte
que la experiencia demuestra que apenas el grave ha abandonado el
reposo, adquiere una velocidad notable y yo digo que esta misma
experiencia pone en claro que los primeros impulsos del grave en
caída,.. Son muy lentos y muy tardos.. Dado que la
velocidad puede ser aumentada o disminuida sin límites,
¿Por qué razón podrá persuadirme de
que en tal móvil, al partir de una lentitud infinita
(reposo) entra inmediatamente en una velocidad de 10 grados mas
bien que en una de 4, o en esta con preferencia a una de 2, de 1,
de ½, o de un centésimo, o en suma, en todas las
menores hasta lo infinito?".

Galileo estaba claro al asegurar que un cuerpo sometido a una
aceleración y partiendo del reposo no adquiere
instantáneamente grandes valores de
velocidad, sino que siendo la razón de cambio de la
velocidad respecto al tiempo una constante, para tiempos muy
pequeños a partir de t=0, el cuerpo solo alcanza
pequeños valores de velocidad. He aquí por que nos
atrevemos a afirmar que Galileo ya esbozaba el concepto de
infinitesimal.

Movimiento Acelerado por Planos Inclinados.

A partir de aquí Galileo realiza un estudio bastante
detallado del MUA que efectúa un móvil que
desciende por un plano inclinado con respecto a la horizontal y
comienza por decir: "acepto que las velocidades de un mismo
móvil; adquiridas sobre diversos planos inclinados son
iguales, cuando las alturas de esos mismos planos son iguales".
Estoes comprobable no solo por las ecuaciones de
la Cinemática, sino por algo mucho más
general, que tampoco era conocido en los tiempos de Galileo y que
es el principio de conservación de la energía
mecánica, el cual se cumple siempre que se
desprecie la fricción.

Galileo demostraba su afirmación a partir de considerar
el ejemplo de un péndulo suspendido de un punto A y que
desplazado hasta el punto C se suelta; analiza el movimiento del
péndulo sin que en su trayectoria curvilínea el
hilo encuentre un obstáculo y después situando
clavos en os puntos E y F (Fig.1). Sobre esta situación
decía: "la caída por el arco CB confiere al
móvil un momentun tal que pueda volverlo a la misma altura
por cualquiera de los arcos BD; BG o BI, no obstante no podemos
nosotros demostrar con la misma evidencia que sucedería lo
mismo, si una bola perfecta debiera descender por planos
inclinados según las inclinaciones de los cuerpos de estos
mismos

arcos, al contrario, es presumible que al formar
ángulos en el punto B esos planos rectos, la bola que ha
descendido por el plano inclinado CB, encontrar obstáculos
en los planos ascendentes según las cuerdas BD; BG o BI,
al chocar con ellas perdería parte de su ímpetu y
no podría subiendo llegar hasta la línea CD. Pero
removido el obstáculo me parece fácil de comprender
que el ímpetu, (que efectivamente adquiere la fuerza con la
cantidad de descenso), sería suficiente para volver al
móvil a la misma altura". Galileo, aunque utilizaba
términos no apropiados, como son: ímpetu

por el concepto de energía cinética, momentun
por el concepto de energía, etc., así describe con
extrema claridad y exactitud tanto el ejemplo del péndulo,
como el de movimiento por el plano inclinado, donde en este
último no olvidó ni siquiera la perfección
de la bola para evitar pérdidas de energía. Es
increíble como el genio de
Galileo asocia dos ejemplos diferentes bajo un mismo
fenómeno: MUA y como selecciona las variables
significativas que describen el fenómeno y lo generaliza,
en fin; como aplica al estudio de fenómenos naturales una
metodología científica.

A partir de los principios
anteriores Galileo deriva una serie de proposiciones o teoremas,
los cuales demuestra a partir de métodos
geométricos y que explican y relacionan
características propias de los MUA. En nuestro trabajo
analizaremos los primeros cinco teoremas.

Teorema I.- "El tiempo en que un móvil recorre un
espacio con MUA a partir del reposo, es igual al tiempo en que el
mismo móvil recorrería ese mismo espacio con
movimiento uniforme, cuya velocidad fuera subdupla (mitad) de la
mayor y ultima velocidad (final) del anterior movimiento
uniformemente acelerado".

Galileo lo demuestra como sigue: en la figura, CD
es el tiempo de caída de un cuerpo que a partir del reposo
(V0=0), alcanza en el punto D un valor de
velocidad proporcional a la línea BE. Si se traza por el
punto medio de BE (punto F), una paralela a AB, triangulo AEB
formado por los incrementos sucesivos de velocidad a partir de
V0=0 y hasta V=EB y por otra parte el rectángulo AGFB
formado en su lado mayor por el tiempo de la caída y en su
base por la mitad de la velocidad final del MUA. Galileo
explicaba "el paralelogramo AGFB es igual al triangulo AEB,.. Es
pues prudente que serán guales los espacios recorridos en
un mismo tiempo por dos móviles, de los cuales uno se
mueve con MUA a partir del reposo y el otro con movimiento
uniforme de velocidad subdupla de la máxima velocidad del
movimiento acelerado". Si a partir del concepto de velocidad
V=dx/dt realizamos la integración para hallar la distancia x
recorrida por los móviles que describen MUA y MRU
respectivamente, tendremos:

Teorema 2.- "Si un móvil con MUA desciende desde el
reposo, los espacios recorridos en tiempos cualesquiera,
están entre si como la razón al cuadrado de los
mismos tiempos, es decir como los cuadrados de esos tiempos".

La demostración realizada por Galileo la describiremos
mas adelante, no obstante vale señalar la veracidad de tal
teorema, e incluso que el mismo pudiera ser el embrión de
la actual relación X=V0t + ½ gt2, ya que si V0 = 0,
queda como X = ½ gt2, donde ½ g es una constante,
por lo que x = kt2, es decir X es proporcional a t2.

Este teorema presenta dos corolarios, los que analizaremos de
inmediato:

Corolario 1.- "Si en tiempos iguales, tomados sucesivamente
desde el primer instante o comienzo del movimiento,…, se
recorren los espacios HL, LM, MN, NI; estos espacios
estarán entre si como los números impares a partir
de la unidad, es decir, como 1, 3, 5, 7,..; porque esta es la
razón de los excesos de los cuadrados de las líneas
que se van extendiendo unas de otras y cuyos excesos es igual a
la menor de ellas ,.., por consiguiente, mientras la velocidad se
acrece, durante tiempos iguales, según la sucesión
simple de los números, los espacios recorridos durante
estos tiempos reciben incrementos según la sucesión
de los números impares, a contar de la unidad".

La línea AG representa los intervalos iguales de tiempo
y la línea HI representa las distintas distancias
recorridas en esos intervalos. Posteriormente se construye el
triangulo APF formado por los valores de
velocidad en los instantes A, D, E, F y que corresponden con 0,
DB, EC, FP y que a la vez cumplen con que se incrementan en la
misma proporción, tal y como se demostró
anteriormente. Las áreas de las figuras ABD, BDCE y CEPF
representan las distancias recorridas a partir del reposo, por un
móvil con MUA están relacionados entre si, por los
números impares 1, 3, 5,.., siempre que se tomen para
intervalos iguales de tiempo: "tomados en conjunto los espacios
recorridos, el recorrido en tiempo doble es cuádruplo del
recorrido en el subduplo; el recorrido en el tiempo triple es
nónuplo y en suma, los espacios recorridos están en
proporción de la segunda potencia de los
tiempos, es decir, como los cuadrados de los tiempos".

Es decir: Si el tiempo se duplica la distancia recorrida se
cuadriplica y si el tiempo se triplica, la distancia recorrida se
nonuplica. Otra vez entonces Galileo vuelve a plantea que X es
proporcional a t2, lo que constituye una de las
características más sobresalientes del MUA.
Aquí podría especularse que si bien Galileo no
planteo ecuaciones matemáticas que relacionaran las diferentes
magnitudes físicas que caracterizan al MUA, las
conocía, sabía que eran sus dependencias y en
última instancia podría estar en principio, en
posibilidades de establecer tales ecuaciones.

Ahora Salviati expone uno de los principios que caracterizaba
a Galileo y a su modo de explicar los fenómenos naturales
y por el cual se dice que el sabio italiano era, sino el
precursor, al menos un asiduo a la experiencia como forma de
corroborar la teoría,
manera de pensar de total vigencia e importancia suprema, que por
desgracia no estuvo presente siempre en todos los antiguos
hombres que trataron de establecer teorías
o regulaciones sobre fenómenos naturales: "es conveniente
hacer en las ciencias que
aplican demostraciones matemáticas a los fenómenos
naturales, como lo hacen los perspectivos, los astrónomos,
los músicos y otros, quienes con experimentos
sensibles confirmaban sus principios, que son los fundamentos de
toda la siguiente estructura".
Veamos ahora el experimento propuesto por Galileo para corroborar
que X es proporcional a t2 y obsérvese su genialidad a la
vez el cuidado en tener presente el más mínimo
detalle.

Se propuso un tablón de l2 codos de largo por ½
codo de alto y tres dedos de ancho; en el centro de su ancho se
construyó un canal derecho, liso y pulido de un dedo de
ancho, por el cual se dejaría deslizar una bola de bronce,
durísima, redonda y pulida; debido a que el tablón
estaba inclinado 1 o 2 brazas. Se dejaba caer la bola y se
registraban los tiempos que demoraba en recorrer el
tablón. Aquí vale destacar que los tiempos eran
medidos mediante un cubo lleno de agua
suspendido en lo alto y de cuyo fondo, mediante un pequeño
conducto, salía el agua que
era recogida en un vaso y pesada en una sensible balanza, es
decir os intervalos de tiempo se hacían corresponder con
los pesos del agua contenida en el vaso, lo que denota genialidad
a la hora de plantear el experimento. Así mismo Galileo
relata que se repetía el experimento muchas veces para
"medir con exactitud el tiempo, en el cual jamás se
encontraba una diferencia ni siquiera de la décima parte
de una pulsación".

Aquí aparece otra característica que está
dada por la repetibilidad del experimento, buscando confiabilidad
en los resultados. Una vez hallado el tiempo total de bajada de
la bola por el plano inclinado (tt), se procedía de igual
forma, pero dejando que la bola solo recorriera la cuarta parte
de la longitud del tablón (ta). De esta forma se
podían comparar los resultados del tiempo y las
distancias, hallándose que:

Esto se repitió para diferentes distancias, (½,
¾,.) y se hicieron más de 100 veces para cada una
de ellas y para diferentes inclinaciones del tablón,
resultando siempre que X es proporcional a t2.

Aquí solo puede criticarse al experimento de Galileo
que no aprovechó la experiencia descrita para constatar
que los incrementos de la velocidad en un mismo intervalo de
tiempo (la aceleración de bajada de la bola)
dependía de la inclinación del tablón y que
aumentaba con ella hasta su valor máximo cuando el
ángulo era de 900; por lo demás esta propia
experiencia puede ser realizada al abordar la enseñanza de este contenido dada la forma
clara con que se obtiene la dependencia entre la distancia
recorrida y el tiempo en un MUA:

Corolario II.- "Si a partir del comienzo del movimiento se
toman dos distancias cualesquiera, recorridas en intervalos
cualesquiera, los tiempos de las mismas serán entre
sí, como cualquiera de ellas a la distancia media
proporcional entre las mismas"

Ahora se observa, como rasgo característico de todo
investigador, o de la forma en que debe presentarse un contenido,
como Galileo avanza de lo simple a lo complejo, de lo
fácil a lo difícil, como va complicando sus propias
hipótesis, buscando relaciones cada vez mas
complejas; pero que en última instancia también son
caracteristicas del fenómeno estudiado.

Galileo continúa su análisis diciendo: "pero habiendo sido
demostrado que los espacios recorridos están en
razón de la segunda potencia de los tiempos,…, y siendo
la razón del espacio VS al espacio ST segunda potencia de
la razón VS a SX, es decir, siendo la misma que la que
tienen los cuadrados VS y SX, es evidente que la razón de
los tiempos de los movimientos por SV, ST es como la de los
espacios o de las líneas VS, SX" lo cual es demostrable
según:

Todo esto demuestra que no solo el pleno dominio que
poseía Galileo del MUA, sino que era capaz de relacionar
matemáticamente las magnitudes que lo caracterizan. Mas
adelante Galileo retoma el ejemplo del plano inclinado de
ángulo variable y comienza a considerar, (con los
conceptos de su época) la variación que experimenta
la aceleración con dicho ángulo; aunque aquí
cabe alertar que Galileo no logra dar gran claridad del concepto
de aceleración y aunque conoce el fenómeno de la
atracción gravitatoria, no lega a precisar el
término de aceleración de la gravedad; así
como tampoco logra definir la aceleración como los cambios
que experimenta la velocidad en un intervalo de tiempo; no
obstante es certero su análisis y llega a resultados
correctos como es el caso de que la línea perpendicular es
por donde el móvil mayor "aceleración" y por ende
mayor velocidad con respecto a otros móviles que se mueven
por trayectorias inclinadas, para intervalos iguales de
tiempo.

Galileo afirmaba: "Comencemos por considerar que los momentos
o velocidades de un mismo móvil son diversos sobre
diversas inclinaciones de planos y que la máxima se
efectúa por la línea elevada perpendicular sobre la
horizontal". Hasta aquí solo se habla de la palabra
momento y es necesario corregir que se trata de iguales
distancias con diferentes inclinaciones, de manera de que en: V2
= V02 + 2aX, mientras que si consideramos V0 = 0, entonces V =
2aX = ka

Continúa Galileo: "por ello el ímpetu, la
disposición, la energía, o si se quiere el momentun
de descenso, es disminuido en el móvil por el plano
infraopuesto, sobre el que ese móvil se apoya y descansa".
Gran cantidad de palabras para expresar que por ser g un
vector dirigido verticalmente hacia abajo, cualquier movimiento
por un plano inclinado en ángulo ? con la horizontal
estará sometido a solo una componente de esa
aceleración y que corresponde con (g sen ?), lo que pone
de manifiesto que Galileo, como dijimos, no tiene claro el
concepto de aceleración.

Veamos la explicación que da a su anterior
afirmación, la cual es plausible: "Digo que el
ímpetu del grave, para descender, es máximo y total
cuando éste desciende pro DA y menor todavía cuando
lo hace por EA y así va sucesivamente disminuyendo por la
dirección mas inclinada FA, hasta quedar
por fin extinguido en la horizontal CA, donde el móvil se
halla indiferente al movimiento o al reposo,.. Así como es
imposible que un cuerpo..se mueva naturalmente hacia arriba,
alejándose del centro común donde tienden todas las
cosas graves, así también es imposible que
él se mueva espontáneamente, si con tal movimiento,
su propio centro de gravedad no se acerca al antedicho centro
común y por ello completamente privado de
inclinación, el ímpetu o memento de dicho
móvil será nulo".

Evidentemente Galileo poseía con claridad el concepto
de atracción gravitatoria, aun cuando faltaban algunos
años para que Newton
formulara esta ley, y el
concepto de equilibrio
indiferente, y la explicación a por qué por la
perpendicular BA es movimiento era más rápido se
puede considerar plausible.

Galileo buscó una relación entre "el cambio de
ímpetu" y la inclinación de los planos, planteando
que: "la línea FC, por la cual es máximo el
ímpetu del grave,.., se inquiere que proporción
tiene ese momento respecto al del mismo móvil por el plano
inclinado FA; digo que tal proporción es la inversa de
dichas longitudes". Lo cual es totalmente cierto, ya que:

Aquí aparecen tres importantes conclusiones de
Galileo:

l.- "Es evidente que el ímpetu de descenso de un grave
será tan grande como sea la resistencia o
fuerza mínima para impedirlo o contenerlo". Que no es otra
cosa que los cambios de velocidad, o sea la aceleración,
es tan grande para un mismo móvil, como sea de
pequeña la fuerza de resistencia o fricción, ya que
el móvil se encuentra bajo los efectos de la
atracción gravitatoria, lo que constituye un enunciado
particular de la segunda ley de Newton, lo cual revela la
grandiosidad de la mente de Galileo.

2.- "El movimiento del móvil G subiendo de A hacia F
está compuesto del componente horizontal AC y del
componente vertical CF", que no es otra cosa que el principio de
independencia
del movimiento, aplicado al movimiento plano.

3.- "Si se ha de dar equilibrio, es decir, reposo entre estos
móviles (H y G), los momentos, las velocidades o su
proporción al movimiento, o sea, los espacios que ellas
recorrerían en un mismo tiempo deben corresponder
inversamente a sus propias gravedades".

Teorema 3.- "Si sobre un plano inclinado y sobre otro
vertical, que tengan la misma altura, marcha un móvil, a
partir del reposo, los tiempos de los descensos serán
entre si, como las longitudes del plano inclinado y el vertical".
Aquí volvemos a lo mismo,

Corolario: "Los tiempos de los descensos por los planos
inclinados de diverso modo, con tal que tengan la misma altura,
son entre si como las longitudes de los mismos planos".
Véase aquí una extensión o
generalización de la conclusión anterior.

Teorema 4.- "Los tiempos de los descensos sobre los planos de
igual longitud, pero desigualmente inclinados, son entre si como
la raíz cuadrada de la razón inversa de las alturas
de los mismos planos".

Teorema 5.- "La razón de los tiempos de los descensos
sobre planos que tienen inclinaciones y longitudes diversas;
así como también alturas desiguales, se compone de
la razón de las longitudes de los planos y de la
raíz cuadrada de la razón de sus alturas, tomadas
inversamente".

Estamos frente a una excelente generalización de los
teoremas 3 y 4 aplicados a un modelo
más general, que plantea que las alturas y las longitudes
de los planos no son iguales; no obstante Galileo persiste en la
relación entre los tiempos, buscando una ecuación o
relación de igual forma; pero que incluya todas las
variantes.

Es evidente que esta obra "Diálogos acerca de dos
nuevas Ciencias", no constituye en si misma un texto
actualizado para la enseñanza de la Física; pero tampoco
es indudable que su estudio nos permite incursionar en la
sabiduría de un hombre, que como muy pocos, supo
adelantarse a su propia época.

Conclusiones

Durante el estudio de esta parte de la obra "Diálogo
acerca de dos nuevas Ciencias" de Galileo Galilei,
se pone en evidencia algunas de las características de
este genial Físico que a nuestro modo de ver no solo le
confiere actualidad, sino que le asigna un gran valor como hombre
de ciencia.

Destaca en la figura de Galileo su extremada osadía
como filósofo, no solo al luchar contra viejas y antiguas
teorías, sino también por el enfrentamiento que
realiza a su propia época y e particular a la temible
inquisición. Su metodología al enfrentar y
desentrañar un fenómeno natural puede asegurarse
que coincide con una metodología científica, siendo
capaz en cada análisis de seleccionar las magnitudes
significativas que lo caracterizan, buscando la relación
entre ellas y avanzando en el estudio de simples proposiciones a
otras mucho mas complejas, todas demostradas con los recursos matemáticos de su época y en
ocasiones con conceptos aún no establecidos; pero que
formaban parte de sus propias concepciones. Otro aspecto a
resaltar en la
personalidad científica de Galileo fue el empleo de la
experiencia como forma de corroborar las nuevas teorías, y
aunque no fue un cuidadoso experimentador, lo que le valió
de poco en las discusiones acerca de sus teorías, si es
innegable su gran genialidad al concebir la forma de
realización de tales experimentos. En algunas partes de su
obra se refleja su criterio respecto a hasta donde llega el
objeto de estudio de la Física y que corresponde a otras
ciencias; observándose que Galileo confiere el papel de:
"arrancar y sacar de las canteras los mármoles, en los
cuales después los artistas y escultores, hacen aparecer
maravillosas imágenes,…"

Es decir, el estudio de las formas mas sencillas del
movimiento y los objetos mas simples, correspondiendo a las
Ciencias Técnicas,
a partir de estos resultados, interpretar y aplicarlos a formas
mas complejas,. Por último, destaca sobremanera la
extraordinaria genialidad de Galileo, tanto para demostrar sus
teorías como para establecerlas, de ahí que resulte
correcto catalogarlo como un gigante de las ciencias dentro de su
época, sobre los hombros del cual otros genios que le
sucedieron pudieron pararse para como él propio Galileo
dijera: "explorar rincones mas remotos".

Bibliografía

Galileo Galilei. Diálogos acerca de dos nuevas
Ciencias. Traducido por José San Román Villasante.
Argentina 1945 (Tomado de un libro italiano
de 1898)

Síntesis Curricular Autor

1.1 Nombre y Apellidos: Antonio O. Pérez de Prado Santa
María.

1.2 Lugar y fecha de nacimiento: Cárdenas, l4 de
diciembre de 1947. Cuba.

1.3 Categoría Docente: Profesor
Auxiliar

1.4 Categoría Científica: Master en Ciencias de la
Educación Superior, mención docencia
universitaria e investigación educativa.

1.5 Dirección Particular: Calle 129 Edificio 13
plantas 2 piso
9 Apto.4 entre 200 y 202 Peñas Altas, Playa, Matanzas,
Cuba.

Teléfono particular 0053 45 261132.

Email:

Graduado de la carrera profesoral, sección
básica, en Física y Química, en el
Instituto Pedagógico Enrique José Varona de la
Universidad de la
Habana, en 1967 y de la carrera profesoral, de nivel superior, en
la especialidad de Física, en el Instituto Superior
Pedagógico de Matanzas en 1977. Desde 1978 hasta la fecha
ha recibido diferentes cursos y estudios de post grado, de la
especialidad y vinculados a la esfera educacional, dentro y fuera
del país, titulándose en 1999 como Master en
Ciencias de la Educación
Superior, ha estado
vinculado y ha dirigido diferentes tareas y temas de investigación, obteniendo un logro
científico en 1995, ha publicado diferentes
artículos en revistas de carácter nacional y fue miembro del
colectivo de autores de dos textos de Pedagogía y de varias monografías
didácticas, ha impartido diferentes cursos y
entrenamientos de post grado y es profesor de Tendencias
Pedagógicas Contemporáneas en la maestría en
Ciencias de la Educación
Superior, impartiendo la asignatura en diferentes versiones de
nuestra Universidad, en la Universidad de Ciego de Ávila y
en países como Brasil, Colombia y
Venezuela, ha
sido tutor de tres tesis y
profesor de la asignatura Gestión
Universitaria y el Rol del Profesor en la Maestría de
Amplio Acceso.

Comenzó su vida laboral en 1967
como funcionario de las oficinas centrales del Ministerio de
Educación,
en 1969 pasa a la Dirección Provincial de Educación
de Matanzas, como inspector provincial de Física, en 1973
comienza a trabajar en el Instituto Superior Pedagógico de
Matanzas, donde fue profesor, asesor y jefe del Dpto. de
Física y en 1976 pasa a la Sede Universitaria, actual
Universidad de Matanzas, donde se ha mantenido durante todos
estos años como profesor, impartiendo Física en las
diferentes especialidades de Ciencias Técnicas y en
Agronomía, así como ha ocupado diferentes
responsabilidades de carácter metodológico y de
dirección. En el curso 2003 -2004 fue jefe de Colectivo de
Física en la Universidad de las Ciencias
Informáticas de Ciudad de la Habana y desde julio del 2006
hasta febrero del 2008 impartió diferentes asignaturas de
Física General y Didáctica de la Física en la
Escuela
Superior Pedagógica de Lunda Norte, de la Universidad
Agostinho Neto de Angola.

Fecha de confección: febrero del
2010

Autor:

Antonio Pérez de Prado