Sistemas de numeración
- Numeración decimal y
binaria - Sistema numérico
binario - Transformación de decimal
a binario - Transformación de
binario a decimal - Suma de números
binarios
Los sistemas de
numeración son las distintas formas de representar la
información numérica. Se nombran
haciendo referencia a la base, que representa el número de
dígitos diferentes para representar todos los
números.
El sistema habitual
de numeración para las personas es el Decimal, cuya base
es diez y corresponde a los distintos dedos de la mano, mientras
que el método
habitualmente utilizado por los sistemas
electrónicos digitales es el Binario, que utiliza
únicamente dos cifras para representar la
información: el 0 y el 1.
Otros sistemas como el Octal (base 8) y el Hexadecimal
(base 16) son utilizados en las computadoras.
Cuando en una numeración se usan diez símbolos diversos, a ésta se la
denomina numeración decimal o en base 10. El
valor de cada
cifra es el producto de la
misma por una potencia a 10 (la
base), cuyo exponente es igual a la posición 0, las
decenas la 1 y así sucesivamente.
Por ejemplo, 327 se puede descomponer en:
3 . 10² + 2 . 10¹ + 7 .
10º = 300 + 20 + 7 = 327
Siguiendo con el mismo razonamiento, podemos definir una
numeración binaria o en base 2, donde los
símbolos 0 y 1 vistos anteriormente asumen el valor
numérico 0 y 1. Así, el número 10110 escrito
en base 2 o binaria equivale al siguiente número en base
10 o decimal:
1 . 24 + 0 . 2³ + 1 . 2² + 1 .
2¹ + 0 . 2º = 16 + 0 + 4 + 2 + 0 = (22)10
En el sistema
binario:
– Con 1 bit el valor más alto que se puede
expresar es el 1.
– Con 2 bits el valor más alto que se puede
expresar es el 3.
– Con n bits el valor más alto que se
puede expresar es el 2 – 1.
Cada bit, según la posición que ocupa
dentro del conjunto de un número binario, tiene un peso o
un valor determinado en el sistema decimal.
Como vemos, el sistema binario emplea muchas cifras para
representar una información. Para poder trabajar
con más comodidad, los programadores emplean los sistemas
octal y hexadecimal, que permiten operar con muchas menos
cifras.
Los circuitos
digitales internos que componen las computadoras utilizan el
sistema de numeración Binario para la interpretación de la información y
codificación de la misma.
El sistema decimal de numeración que usamos en la
vida diaria es de difícil empleo en las
computadoras, ya que para representar los números y
trabajar con ellos son necesarios diez
símbolos:
0 1 2 3 4 5 6 7 8 9
Los circuitos de una computadora
que trabajara con el sistema decimal deberían ser capaces
de distinguir entre diez valores o
posiciones de funcionamiento distintas. Esto exigiría una
precisión difícil de conseguir, por lo que se ha
elegido un sistema de numeración que simplifica mucho el
diseño
de los circuitos, porque exige sólo dos estados o
posiciones de funcionamiento.
El sistema binario utiliza sólo dos signos:
0 1
Estos son mucho más fáciles de representar
en el interior de una computadora, donde estas dos cifras se
pueden asociar perfectamente a los dos posibles estados que
pueden adoptar los circuitos o componentes electrónicos:
apagado y encendido. La presencia de una corriente
eléctrica = 1 (encendido) y la ausencia = 0 (apagado).
Cuando la corriente eléctrica pasa a través de
la
computadora, ésta lee un 1 cuando percibe la corriente
eléctrica y un 0 cuando no hay corriente
eléctrica.
A las cifras o símbolos binarios les
denominaremos, por convención, bits.
bit cero = 0
bit uno = 1
La palabra «bit» es una contracción
de las palabras inglesas binary digit, dígito
binario.
El bit es la unidad más pequeña de
información. Aislado, nos permite distinguir sólo
entre dos posibilidades: sí-no, blanco-negro,
abierto-cerrado, positivo-negativo. Permite sólo dar dos
respuestas a una pregunta, sin matices.
La combinación de estos dos símbolos un
determinado número de veces permite la codificación
de toda la información posible. Si codificamos una serie
de bits dándole a cada uno un significado según
nuestro deseo, el cojunto de bits representa un conjunto de
información.
Por consiguiente, si sustituimos el valor dado a cada
bit por otro, tendremos que una misma combinación de bits
queda modificada en cuanto al significado:
– Con un solo bit, se representan dos informaciones o
estados (2¹).
– Con dos bits (2²), obtenemos cuatro combinaciones
de información.
– Con tres bits (2³), ocho combinaciones de
información.
– Con cuatro bits (24), dieciséis combinaciones
de información.
– Con n bits, (2n) combinaciones de
información.
Si deseamos representar cada letra del alfabeto mediante
una combinación de bits, necesitamos que cada letra
esté representada por lo menos por 5 bits (25 = 32). Si,
además, deseamos abarcar todos los signos gráficos y las letras, tanto
minúsculas como mayúsculas, necesitaremos una
combinación de 7 bits (27 = 128).
TRANSFORMACIÓN DE DECIMAL A
BINARIO
Para cambiar un número decimal a número
binario, se divide el número entre dos. Se escribe el
cociente y el residuo. Si el cociente es mayor que uno, se divide
el cociente entre dos. Se vuelve a escribir el cociente y el
residuo. Este proceso se
sigue realizando hasta que el cociente sea uno. Cuando el
cociente es uno, se escribe el cociente y el residuo. Para
obtener el número binario, una vez llegados al 1
indivisible, se cuentan el último cociente, es decir el
uno final (todo número binario excepto el 0 empieza por
uno), seguido de los residuos de las divisiones subsiguientes.
Del más reciente hasta el primero que resultó. Este
número será el binario que buscamos. A
continuación analizaremos dos ejemplos de números
decimales transformados al sistema binario:
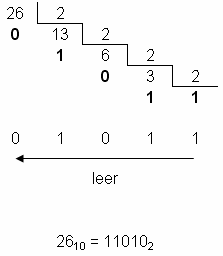
NÚMERO DECIMAL 26
TRANSFORMADO AL SISTEMA BINARIO
NÚMERO DECIMAL 8
TRANSFORMADO AL SISTEMA BINARIO
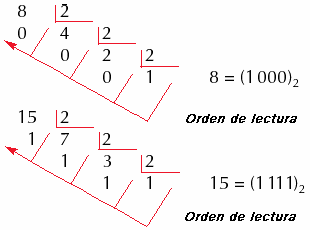
Recordemos que se comienza a contar desde el cociente 1
hasta el primer residuo que nos resultó. Sin embargo,
existe otra manera de hacerlo y es dividir el cociente 1 entre 2,
escribimos 0 como cociente, posteriormente multiplicamos 2 por 0
(que es cero) y ese resultado se lo restamos al último
residuo que teníamos (que será 1) y tendremos como
residuo 1. De esta forma comenzaremos la cuenta para obtener el
valor binario desde el último residuo obtenido (que es
siempre 1, excepto en el caso del número 0) hasta el
primero. Podemos utilizar cualquiera de los dos métodos y
ambos son correctos y presentan el último resultado, tal
como veremos en los ejemplos a continuación.
Ahora veremos tres nuevos ejemplos de
transformación de un número del sistema decimal al
sistema binario:



TRANSFORMACIÓN DE BINARIO A
DECIMAL
Para cambiar un número binario a número
decimal se multiplica cada dígito binario por la potencia
y se suman. Para conseguir el valor de la potencia, usamos
![]() , donde
, donde ![]() es la base y
es la base y ![]() es el exponente. Como
es el exponente. Como
estamos cambiando de binario a decimal, usamos la base 2. El
exponente nos indica la posición del dígito. A
continuación se transformará el número
binario 11010 a decimal:
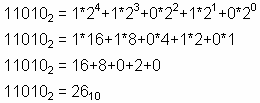
Para la transformación de binarios a decimales
estaremos siempre utilizando potencias a las cuales será
elevado el número 2. El siguiente listado nos presenta
progresivamente las primeras 20 potencias con base 2:
LISTA DE POTENCIACIÓN DEL 1
AL 20 CON BASE 2

Veamos tres nuevos ejemplos de transformación de
un número del sistema decimal al sistema
binario:



NÚMEROS DECIMALES DEL 0 AL
10 Y SUS EQUIVALENTES EN BINARIO

Es similar a la suma decimal excepto que se manejan
sólo dos dígitos (0 y 1).
Las sumas básicas son:

Por ejemplo, sumemos 100110101 + 11010101:

Operamos como en decimal: comenzamos a sumar desde la
izquierda. En el ejemplo 1 + 1 = 10, entonces escribimos 0 y
"llevamos" 1. Se suma este 1 a la siguiente columna: 1 + 0 + 0 =
1, y seguimos hasta terminar todas las columnas (exactamente como
en decimal).
Ahora presentamos 3 nuevos ejemplos de suma de
números binarios en los cuales podremos apreciar al lado
de dichas operaciones, el
equivalente de esa suma en el sistema decimal para facilitar la
comprensión:



CUATRO EJERCICIOS DE SUMA DE
NÚMEROS BINARIOS
1. Dados los números 30, 35 y 22 en sistema
decimal, efectuar la suma y expresar el resultado en el sistema
de numeración binaria.
a) Conversión de 30 a binario.
División Cociente Residuo
30 / 2 = 15 0
15 / 2 = 7 1
7 / 2 = 3 1
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 30 en el sistema decimal equivale a 11110 en el
sistema binario.
b) Conversión de 35 a binario.
División Cociente Residuo
35 / 2 = 15 0
17 / 2 = 8 1
8 / 2 = 3 1
4 / 2 = 1 1
2 / 2 = 0 1
1 / 2 = 0 1
Entonces 35 en el sistema decimal equivale a 100011 en
el sistema binario.
c) Conversión de 22 a binario.
División Cociente Residuo
22 / 2 = 11 0
11 / 2 = 5 1
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 22 en el sistema decimal equivale a 10110 en el
sistema binario.
d) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
30+ 11110+
35 100011
22= 10110=
87 1010111
2. Sumar los números decimales 100 y 51,
expresando la operación y el resultado en números
binarios.
a) Conversión de 100 a binario.
División Cociente Residuo
100 / 2 = 50 0
50 / 2 = 25 0
25 / 2 = 12 1
12 / 2 = 6 0
6 / 2 = 3 0
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 100 en el sistema decimal equivale a 1100100 en
el sistema binario.
b) Conversión de 51 a binario.
División Cociente Residuo
51 / 2 = 25 1
25 / 2 = 12 1
12 / 2 = 6 0
6 / 2 = 3 0
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 51 en el sistema decimal equivale a 110011 en
el sistema binario.
c) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
100+ 1100100+
51= 110011=
151 10010111
3. Teniendo los valores
42, 6 y 8 en sistema decimal, transformarlos y expresarlos en
números binarios.
a) Conversión de 42 a binario.
División Cociente Residuo
42 / 2 = 21 0
21 / 2 = 10 1
10 / 2 = 5 0
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 42 en el sistema decimal equivale a 101010 en
el sistema binario.
b) Conversión de 6 a binario.
División Cociente Residuo
6 / 2 = 3 0
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 6 en el sistema decimal equivale a 110 en el
sistema binario.
c) Conversión de 8 a binario.
División Cociente Residuo
8 / 2 = 4 0
4 / 2 = 2 0
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 8 en el sistema decimal equivale a 1000 en el
sistema binario.
d) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
42+ 101010+
6 110
8= 1000=
56 111000
4. Sumar los números decimales 8, 17, 60, 40 y
30, convirtiéndolos y expresando la operación y
resultado de la suma en números binarios.
a) Conversión de 8 a binario.
División Cociente Residuo
8 / 2 = 4 0
4 / 2 = 2 0
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 8 en el sistema decimal equivale a 1000 en el
sistema binario.
b) Conversión de 17 a binario.
División Cociente Residuo
17 / 2 = 8 1
8 / 2 = 3 1
4 / 2 = 1 1
2 / 2 = 0 1
1 / 2 = 0 1
Entonces 17 en el sistema decimal equivale a 11111 en el
sistema binario.
c) Conversión de 60 a binario.
División Cociente Residuo
60 / 2 = 30 0
30 / 2 = 15 0
15 / 2 = 7 1
7 / 2 = 3 1
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 60 en el sistema decimal equivale a 111100 en
el sistema binario.
d) Conversión de 40 a binario.
División Cociente Residuo
40 / 2 = 20 0
20 / 2 = 10 0
10 / 2 = 5 0
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 40 en el sistema decimal equivale a 101000 en
el sistema binario.
e) Conversión de 30 a binario.
División Cociente Residuo
30 / 2 = 15 0
15 / 2 = 7 1
7 / 2 = 3 1
3 / 2 = 1 1
1 / 2 = 1 1
Entonces 30 en el sistema decimal equivale a 11110 en el
sistema binario.
f) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
8+ 1000+
17 10001
60 111100
40 101000
30= 11110=
155 10011011
GUÍA DE DIEZ EJERCICIOS DE
SUMA DE NÚMEROS BINARIOS
INDICACIÓN: Dados los siguientes
valores del sistema numérico decimal, convertir cada uno
de ellos a números binarios y luego sumarlos, expresando
la respuesta en el sistema numérico
binario.
1. Sumar 4 + 5 +10.
2. Sumar 40 + 91.
3. Sumar 1203 + 101.
4. Sumar 59 + 21.
5. Sumar 5 + 2 + 6.
6. Sumar 25 + 31.
7. Sumar 40 + 31 + 20 + 49.
8. Sumar 8 + 9 + 98 + 45 + 11 + 3.
9. Sumar 7 + 16 + 1.
10. Sumar 27 + 8 + 31.
SOLUCIÓN DE LA GUÍA
DE EJERCICIOS
1. Sumar 4 + 5 + 10.
a) Conversión de 4 a binario.
División Cociente Residuo
4 / 2 = 2 0
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 4 en el sistema decimal equivale a 100 en el
sistema binario.
b) Conversión de 5 a binario.
División Cociente Residuo
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 5 en el sistema decimal equivale a 101 en el
sistema binario.
c) Conversión de 10 a binario.
División Cociente Residuo
10 / 2 = 5 0
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 10 en el sistema decimal equivale a 1010 en el
sistema binario.
d) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
4+ 100+
5 101
10= 1010=
19 10011
2. Sumar 40 + 91.
a) Conversión de 40 a binario.
División Cociente Residuo
40 / 2 = 20 0
20 / 2 = 10 0
10 / 2 = 5 0
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 40 en el sistema decimal equivale a 101000 en
el sistema binario.
b) Conversión de 91 a binario.
División Cociente Residuo
91 / 2 = 45 1
45 / 2 = 22 1
22 / 2 = 11 0
11 / 2 = 5 1
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 91 en el sistema decimal equivale a 1011011 en
el sistema binario.
c) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
40+ 101000+
91= 1011011=
131 10000011
3. Sumar 1203 + 101.
a) Conversión de 1203 a binario.
División Cociente Residuo
1203 / 2 = 601 1
601 / 2 = 300 1
300 / 2 = 150 0
150 / 2 = 75 0
75 / 2 = 37 1
37 / 2 = 18 1
18 / 2 = 9 0
9 / 2 = 4 1
4 / 2 = 2 0
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 1203 en el sistema decimal equivale a
10010110011 en el sistema binario.
b) Conversión de 101 a binario.
División Cociente Residuo
101 / 2 = 50 1
50 / 2 = 25 0
25 / 2 = 12 1
12 / 2 = 6 0
6 / 2 = 3 0
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 101 en el sistema decimal equivale a 1100101 en
el sistema binario.
c) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
1203+ 10010110011+
101= 1100101=
1304 10100011000
4. Sumar 59 + 21.
a) Conversión de 59 a binario.
División Cociente Residuo
59 / 2 = 29 1
29 / 2 = 14 1
14 / 2 = 7 0
7 / 2 = 3 1
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 59 en el sistema decimal equivale a 111011 en
el sistema binario.
b) Conversión de 21 a binario.
División Cociente Residuo
21 / 2 = 10 1
10 / 2 = 5 0
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 21 en el sistema decimal equivale a 10101 en el
sistema binario.
c) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
59+ 111011+
21= 10101=
80 1010000
5. Sumar 5 + 2 + 6.
a) Conversión de 5 a binario.
División Cociente Residuo
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 5 en el sistema decimal equivale a 101 en el
sistema binario.
b) Conversión de 2 a binario.
División Cociente Residuo
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 2 en el sistema decimal equivale a 10 en el
sistema binario.
c) Conversión de 6 a binario.
División Cociente Residuo
6 / 2 = 3 0
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 6 en el sistema decimal equivale a 110 en el
sistema binario.
d) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
5+ 100+
2 101
6= 1010=
13 1101
6. Sumar 25 + 31.
a) Conversión de 25 a binario.
División Cociente Residuo
25 / 2 = 12 1
12 / 2 = 6 0
6 / 2 = 3 0
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 25 en el sistema decimal equivale a 11001 en el
sistema binario.
b) Conversión de 31 a binario.
División Cociente Residuo
31 / 2 = 15 1
15 / 2 = 7 1
7 / 2 = 3 1
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 21 en el sistema decimal equivale a 11111 en el
sistema binario.
c) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
25+ 11001+
31= 11111=
56 111000
7. Sumar 40 + 31 + 20 + 49.
a) Conversión de 40 a binario.
División Cociente Residuo
40 / 2 = 20 0
20 / 2 = 10 1
10 / 2 = 5 0
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 40 en el sistema decimal equivale a 101010 en
el sistema binario.
b) Conversión de 31 a binario.
División Cociente Residuo
31 / 2 = 15 1
15 / 2 = 7 1
7 / 2 = 3 1
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 31 en el sistema decimal equivale a 11111 en el
sistema binario.
c) Conversión de 20 a binario.
División Cociente Residuo
20 / 2 = 10 0
10 / 2 = 5 0
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 20 en el sistema decimal equivale a 10100 en el
sistema binario.
d) Conversión de 49 a binario.
División Cociente Residuo
49 / 2 = 24 1
24 / 2 = 12 0
12 / 2 = 6 0
6 / 2 = 3 0
3 / 2 = 1 1
Entonces 49 en el sistema decimal equivale a 10001 en el
sistema binario.
e) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
40+ 101000+
31 11111
20 10100
49= 110001=
140 10001100
8. Sumar 8 + 9 + 98 + 45 + 11 + 3.
a) Conversión de 8 a binario.
División Cociente Residuo
8 / 2 = 4 0
4 / 2 = 2 0
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 8 en el sistema decimal equivale a 1000 en el
sistema binario.
b) Conversión de 8 a binario.
División Cociente Residuo
9 / 2 = 4 1
4 / 2 = 2 0
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 9 en el sistema decimal equivale a 1001 en el
sistema binario.
c) Conversión de 98 a binario.
División Cociente Residuo
98 / 2 = 49 0
49 / 2 = 24 1
24 / 2 = 12 0
12 / 2 = 6 0
6 / 2 = 3 0
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 98 en el sistema decimal equivale a 1100010 en
el sistema binario.
d) Conversión de 45 a binario.
División Cociente Residuo
45 / 2 = 22 1
22 / 2 = 11 0
11 / 2 = 5 1
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 45 en el sistema decimal equivale a 101101 en
el sistema binario.
e) Conversión de 11 a binario.
División Cociente Residuo
11 / 2 = 5 1
5 / 2 = 2 1
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 11 en el sistema decimal equivale a 1011 en el
sistema binario.
f) Conversión de 33 a binario.
División Cociente Residuo
3 / 2 = 1 1
1 / 2 = 1 1
Entonces 3 en el sistema decimal equivale a 11 en el
sistema binario.
g) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
8+ 1000+
9 1001
98 1100010
45 101101
11 1011
3= 11=
174 10101110
9. Sumar 7 + 16 + 1.
a) Conversión de 7 a binario.
División Cociente Residuo
7 / 2 = 3 1
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 7 en el sistema decimal equivale a 111 en el
sistema binario.
b) Conversión de 16 a binario.
División Cociente Residuo
16 / 2 = 8 0
8 / 2 = 4 0
4 / 2 = 2 0
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 16 en el sistema decimal equivale a 10000 en el
sistema binario.
c) Conversión de 1 a binario.
División Cociente Residuo
1 / 2 = 0 1
Entonces 1 en el sistema decimal equivale a 1 en el
sistema binario.
e) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
7+ 101000+
16 11111
1= 110001=
24 11000
10. Sumar 27 + 8 + 31.
a) Conversión de 27 a binario.
División Cociente Residuo
27 / 2 = 13 1
13 / 2 = 6 1
6 / 2 = 3 0
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 27 en el sistema decimal equivale a 11011 en el
sistema binario.
b) Conversión de 8 a binario.
División Cociente Residuo
8 / 2 = 4 0
4 / 2 = 2 0
2 / 2 = 1 0
1 / 2 = 0 1
Entonces 8 en el sistema decimal equivale a 1000 en el
sistema binario.
c) Conversión de 31 a binario.
División Cociente Residuo
31 / 2 = 15 1
15 / 2 = 7 1
7 / 2 = 3 1
3 / 2 = 1 1
1 / 2 = 0 1
Entonces 31 en el sistema decimal equivale a 11111 en el
sistema binario.
e) Efectuar la suma de los números binarios
obtenidos.
Decimal Binario
27+ 11011+
8 1000
31= 1000111=
66 1000010
– MENTOR INTERACTIVO. Enciclopedia Temática
Estudiantil. Páginas 184-186. Barcelona, España.
Grupo
Editorial OCEANO.
– MONOGRAFÍAS.COM
http://www.monografias.com/trabajos16/representacion-informacion/representacion-informacion
– WIKIPEDIA.ORG
http://es.wikipedia.org/wiki/Binario
– 100CIA.COM
http://100cia.com/enciclopedia/sistema_binario1.htm
Jaime Oswaldo Montoya Guzmán
Nivel educativo: Estudiante de segundo ciclo de
la carrera Ingeniería en Sistemas
Informáticos.
Centro de estudios: Universidad
Católica de Occidente.
Santa Ana.
El Salvador