Modelos matemáticos-fisiológicos para estimar materia seca da parte aérea e produtividade de grãos d (página 2)

Para determinar a variação da matéria seca durante o ciclo da cultura de milho e estimar o rendimento de grãos foi realizado um experimento inteiramente casualizado, com três repetições, na área experimental da ESALQ, USP, em Piracicaba, SP (22º42’ S, 47º38’ W e 546 m de altitude). A semeadura foi realizada em 20 de outubro de 1997, utilizandose três híbridos comerciais (C-901, C-333-B e C-806), em um solo classificado como NITOSSOLO VERMELHO Eutroférrico.

A colheita foi realizada em 11 de março de 1998. As parcelas constaram de 3,6 m de largura (4 linhas com espaçamento de 0,9 m) com 30 m de comprimento. Cada híbrido ocupou 108 m² por repetição (324 m² por híbrido). Foram utilizadas as populações de 60.000, 50.000 e 50.000 plantas ha^-1 para os híbridos comerciais C-901, C-333-B e C-806, respectivamente.

Para a determinação da matéria seca, foram coletadas 15 plantas por híbrido (5 plantas por repetição) por época (sete épocas de coleta para análise de crescimento referentes aos híbridos C-901 e C-806; oito para C-333-B). Em função da grande quantidade de plantas coletadas, procedeu-se inicialmente a pré-secagem dos diferentes órgãos da planta no interior da casa-de-vegetação do Departamento de Produção Vegetal. Posteriormente, procedeu-se a secagem utilizando o método padrão de estufa com circulação de ar forçado e temperatura regulada para 60ºC.

A fenologia foi observada diariamente e a análise de crescimento foi realizada em intervalos de 15 dias. O desenvolvimento relativo da cultura foi computado desde a emergência até o ponto de maturidade fisiológica através das seguintes equações:

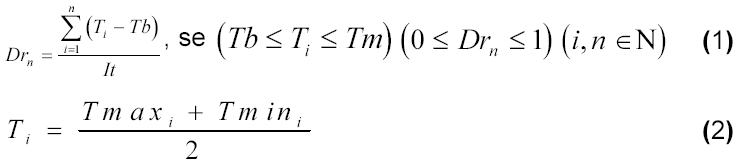
em que Dr_n refere-se ao desenvolvimento relativo acumulado da cultura até o n-ésimo dia após a emergência, T_i à temperatura média do ar (^oC) (se T_i>Tm, faz-se T_i=Tm para efeito de cálculo), Tmax_i e Tmin_i às temperaturas (^oC) máxima e mínima do ar, It ao índice térmico (^oC.dia), Tb e Tm às temperaturas basal inferior (10^oC) e superior (30^oC) da cultura no i-ésimo dia após a emergência, respectivamente.

Foram descritas assunções para obtenção do modelo do cosseno (Tabela 1), sendo que esse modelo foi proposto para prever a variação temporal diária da matéria seca relativa total (Wr_i) da parte aérea da planta:

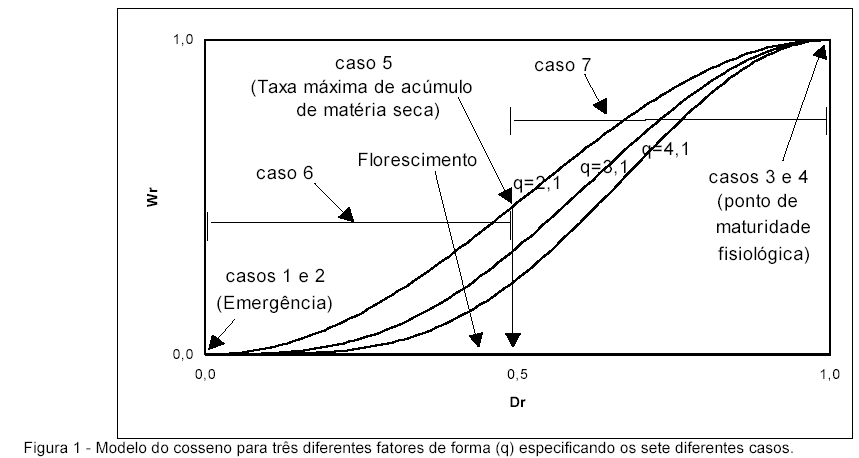
em que Wi e Wm se referem à matéria seca total, por unidade de área (kg m^-2), da parte aérea no i-ésimo dia após a emergência e no ponto de maturidade fisiológica, respectivamente, e q ao fator de forma da curva de crescimento (Figura 1).

Para estimar o fator de forma (q), através de análise de regressão não linear, utilizou-se o método iterativo de Newton- Raphson, devido a impossibilidade de obtenção de uma solução analítica (BARROS, 1976; MIRSHAWKA, 1989):

No intuito de obter um menor número de iterações, utilizou-se o procedimento de anamorfose (ou procedimento de linearização) para calcular o valor inicial do fator de forma q₀ (BARROS, 1976; MIRSHAWKA, 1989):

Para estimativa do desenvolvimento relativo da cultura referente à taxa máxima de acúmulo de matéria seca (Dr_a,kg m^-2 dia^-1) e ao florescimento (Dr_f, kg m^-2 dia^-1), foram utilizadas as seguintes equações:

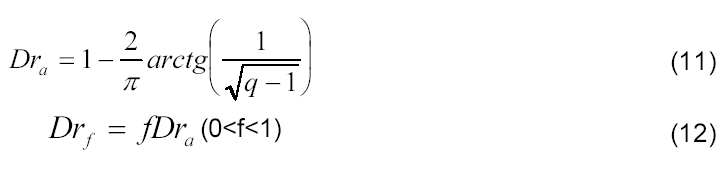
em que f é o fator empírico de conversão do desenvolvimento relativo referente à taxa máxima de acúmulo de matéria seca ao desenvolvimento relativo da cultura referente ao florescimento; logo os modelos extrapoláveis propostos para estimativa da matéria seca da cultura de milho foram os seguintes (Equações 13 e 14):

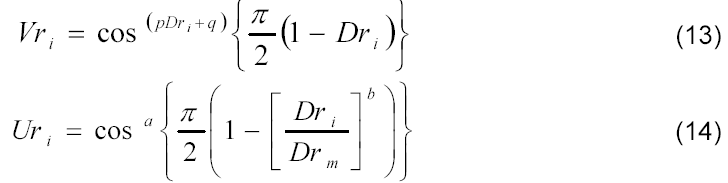
em que Dr se refere ao desenvolvimento relativo; Vr ao valor relativo de matéria seca de colmo, espiga e parte aérea (modelo proposto); Ur ao valor relativo de matéria seca de folha e pendão (modelo proposto); a, b, p, q e Dr_m aos parâmetros empíricos obtidos por de análise de regressão não linear.

A dedução dos modelos (tipos I e II) referentes à variação de matéria seca relativa e do índice relativo de área foliar, em função do desenvolvimento relativo da cultura de milho, expressam matematicamente o conhecimento do fenômeno para fins de previsão com erro de estimativa associado. Os valores relativos foram concebidos no intuito de tornar possível a extrapolação dos resultados obtidos no experimento descrito no presente trabalho.

No modelo (tipo I) avaliou-se a variação de matéria seca relativa do colmo, espiga e parte aérea. Em função do prévio conhecimento do fenômeno a ser modelado, concebeu-se o seguinte modelo (tipo I) básico:

em que Dr_i se refere ao desenvolvimento relativo da cultura e Vr_i ao valor relativo de matéria seca do colmo, espiga e parte aérea no i-ésimo dia após a emergência.

Os valores extremos previamente conhecidos podem ser facilmente verificados, ou seja, (i) quando o desenvolvimento relativo é nulo (Dr_i = 0), na emergência (estádio fenológico 0), o valor relativo de matéria seca do colmo, da espiga e da parte aérea é considerado desprezível (Vr_i = 0); (ii) quando o desenvolvimento relativo é máximo (Dr_i = 1), no ponto de maturidade fisiológica (estádio fenológico 10), o valor relativo de matéria seca do colmo, da espiga e da parte aérea é considerado máximo (Vr_i = 1). Sendo assim, foram inseridos os fatores empíricos de forma (p e q) da curva referente à variação de matéria seca relativa e do índice relativo de área foliar em função do desenvolvimento relativo da cultura de milho, obtendo-se assim o seguinte modelo:

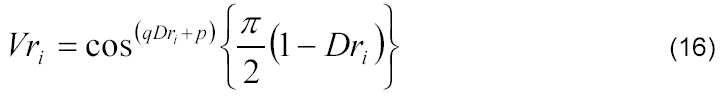
em que 'p' e 'q' se referem aos parâmetros empíricos adimensionais obtidos por meio de análise de regressão não linear minimizando-se a soma dos quadrados dos desvios.

O modelo (tipo I) ainda contempla as seguintes hipóteses básicas: (i) a matéria seca relativa, em função do desenvolvimento relativo da cultura, é uma função estritamente crescente; (ii) a taxa de acúmulo é nula na emergência (estádio 0) e no ponto de maturidade fisiológica (estádio 10); e (iii) a máxima taxa de acúmulo ocorre durante o ciclo da cultura entre a emergência e o ponto de maturidade fisiológica (função sigmoidal).

Para verificação das hipóteses básicas tem-se que:

Para derivação da máxima taxa de acúmulo de matéria seca, referente ao desenvolvimento relativo da cultura, tem-se que:

Procedimento análogo ao anterior foi utilizado para obtenção do modelo (tipo II) básico referente a variação da matéria seca relativa da folha e do pendão:

em que Ur_i se refere ao valor relativo de matéria seca da folha e do pendão no i-ésimo dia após a emergência (cabe salientar que os valores de Dr_m são diferentes para folha e pendão).

Os valores extremos previamente conhecidos podem ser facilmente verificados, ou seja, (i) quando o desenvolvimento relativo é nulo (Dr_i = 0), na emergência (estádio fenológico 0), o valor relativo de matéria seca da folha e do pendão também é considerada desprezível (Ur_i = 0); (ii) numa determinada fase do ciclo, o desenvolvimento relativo (Dr_i = Dr_m) é correspondente ao máximo valor relativo de matéria seca da folha e do pendão (Ur_i = 1); e (iii) quando o desenvolvimento relativo é máximo (Dr_i = 1), no ponto de maturidade fisiológica (estádio fenológico 10), o valor relativo de matéria seca da folha e do pendão decaem (0 < Ur_i < 1).

Sendo assim, foram inseridos os fatores empíricos de forma (Dr_m, a e b) da curva referente à variação de matéria seca relativa da folha e do pendão e do índice relativo de área foliar em função do desenvolvimento relativo da cultura de milho, obtendo-se assim o seguinte modelo:

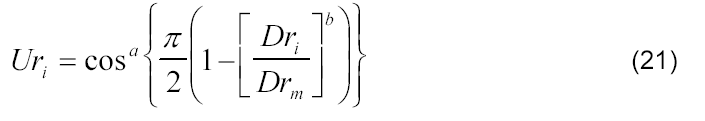
em que Dr_m, a e b se referem aos parâmetros empíricos adimensionais obtidos por de análise de regressão não linear minimizando-se a soma dos quadrados dos desvios.

O modelo (tipo II) contempla as seguintes hipóteses básicas: (i) a matéria seca em função do desenvolvimento relativo da cultura, é uma função estritamente crescente até o desenvolvimento relativo Dr_m, (valor relativo máximo referente à matéria seca), com posterior decréscimo até o ponto de maturidade fisiológica; (ii) a taxa de acúmulo é nula na emergência (estádio 0) e no desenvolvimento relativo Dr_m; (iii) a taxa de acúmulo é negativa no ponto de maturidade fisiológica (estádio 10); e (iv) a máxima taxa de acúmulo ocorre durante o ciclo da cultura entre a emergência e o desenvolvimento relativo Dr_m (função sigmoidal).

Analogamente ao procedimento anterior (equações 15 a 19), para verificação das hipóteses do modelo, tem-se:

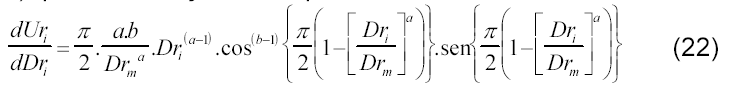
Sendo assim, o ponto de inflexão ocorre quando (máxima taxa de acúmulo de matéria seca da folha e do pendão, em função do desenvolvimento relativo da cultura):

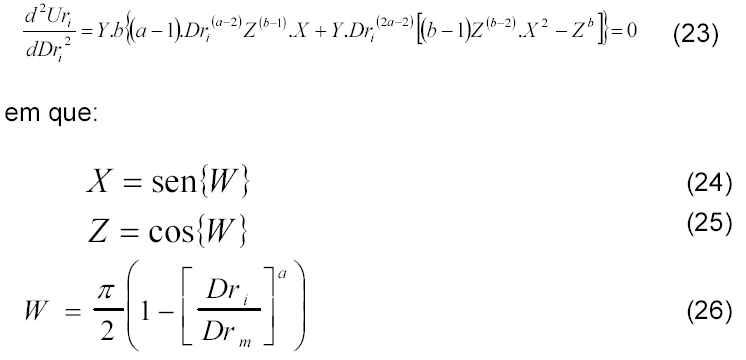
Para estimativa do rendimento tem-se o seguinte modelo:

em que 'R' se refere ao rendimento de grãos (kg ha^-1), 'P' à população de plantas (plantas ha^-1), 'Pr' à prolificidade média (espigas planta^-1), 'Fe' ao número médio de fileiras por espiga (fileiras espiga^-1), 'Gf' ao número médio de grãos por fileira (grãos fileira^-1) e 'Mg' à massa média do grão (g.grão^-1).

Outro modelo qualitativo referente à estimativa de rendimento é de que, a rigor, tem-se inicialmente que estimar a produtividade da cultura numa condição edafoclimática supostamente representativa de uma propriedade ou região.

Essa produtividade será limitada apenas pelo material genético e pela condição climática. Sendo assim, o rendimento será sempre inferior à produtividade ou, no máximo, igual (condição ideal de manejo), o qual pode assim ser definido:

em que R se refere ao rendimento (kg ha^-1), P à produtividade potencial (kg ha^-1), e f ao fator adimensional redutor da produtividade potencial. A rigor, na prática (ao nível de propriedade), a produtividade potencial não é observável. Por outro lado, os modelos quantitativos existentes estimam o fator redutor de produtividade contemplando apenas algumas relações isoladas, e raramente as considera associadas.

O procedimento científico usual é estimar o efeito de uma interação de interesse isoladamente, mantendo as demais supostamente constantes e em condições ótimas. Por essa razão, a informação de pesquisa é sempre uma definição de ordem de grandeza. Por outro lado, apesar dessa limitação, o pesquisador deve explicitar os resultados de forma extrapolável utilizando, sempre que possível, grandezas intensivas (usualmente as grandezas intensivas são obtidas pela relação entre duas grandezas extensivas no intuito de extrapolar e/ou comparar resultados).

Para caracterizar a variação temporal do teor de água na semente botânica, utilizou-se o seguinte modelo:

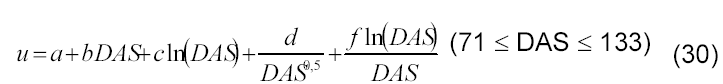
(30) em que a, b, c, d e f se referem aos parâmetros empíricos do modelo, u, ao teor de água a base de massa (g por 100g) base úmida), e DAS o número de dias após a semeadura.

Os modelos explanatórios (modelos estritamente estatísticos) foram obtidos no intuito de se obter curvas referentes à cultura de milho que melhor minimizam a soma dos quadrados dos desvios. Para tal, adotou-se a soma térmica (GD, ºC.dia) da cultura como variável independente e a matéria seca (colmo, folha, pendão, espiga) como variável dependente. O modelo estritamente estatístico é limitado pela sua concepção (extrapolação limitada), e a sua aplicabilidade é restrita a explicar apenas os dados observados ou prever processos ou valores de atributos em condições similares às condições estudadas.

O presente modelo (modelo universal tipos I e II) é utilizável em agricultura irrigada (quando não ocorre deficiência hídrica). Foram selecionados três híbridos comerciais com boa faixa de variação de soma térmica referente ao florescimento, pois a pesquisa tem como função básica estabelecer procedimentos válidos e definir a ordem de grandeza dos valores de interesse, os quais devem ser ajustados para cada caso específico. Apesar das limitações existentes, a soma térmica é uma importante ferramenta para definição da época de semeadura e do híbrido a ser utilizado.

Em agricultura irrigada e em regiões de clima tropical, define-se a época de semeadura e a época de florescimento para cada híbrido segundo a sua adaptação às condições climáticas locais, sendo escolhido o híbrido que floresce mais próximo do número ideal de dias previamente definido. A definição de população e distribuição (espaçamento entre fileiras) de plantas é dependente da arquitetura da planta e, principalmente, da fertilidade do solo. Por sua vez, em agricultura de sequeiro, a definição da população e distribuição de plantas, época de semeadura e híbrido, dependem basicamente do nível de estresse híbrido na época do florescimento (cerca de 10 a 15 dias antes e depois do estádio 5).

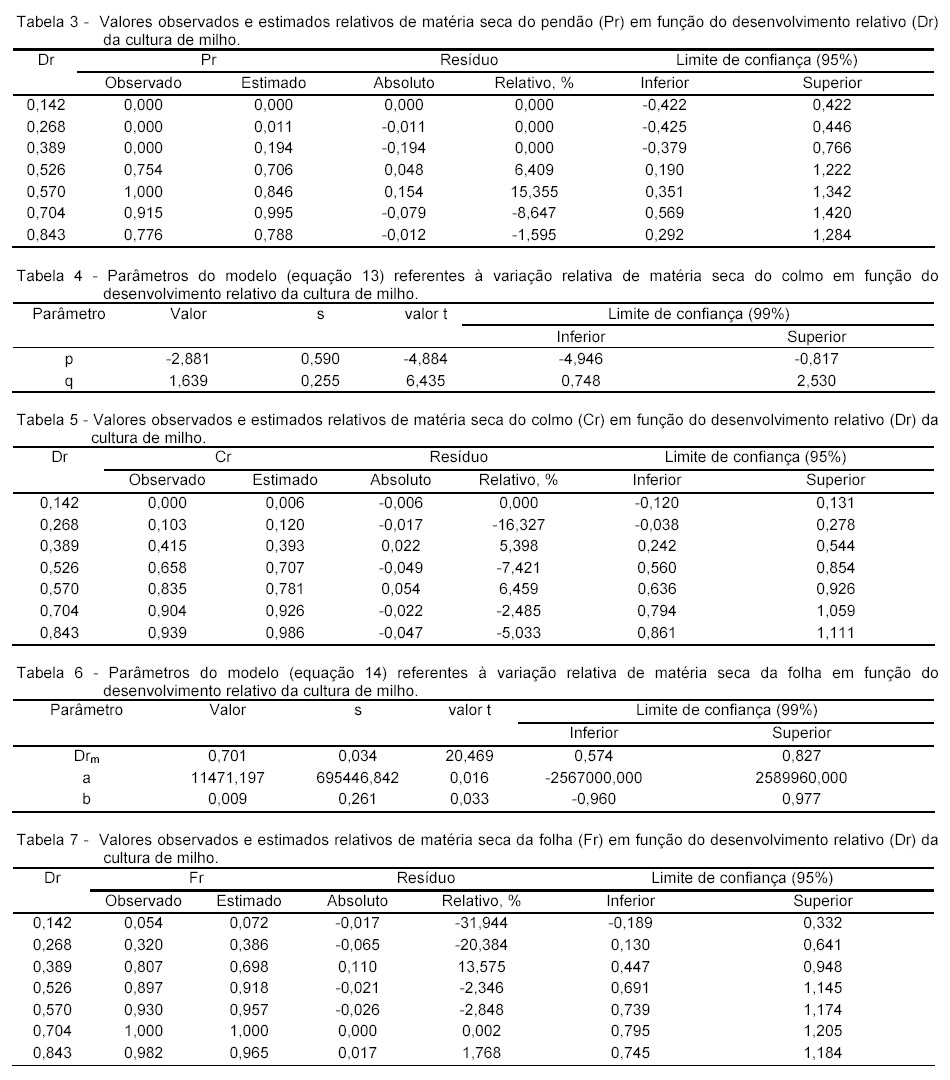
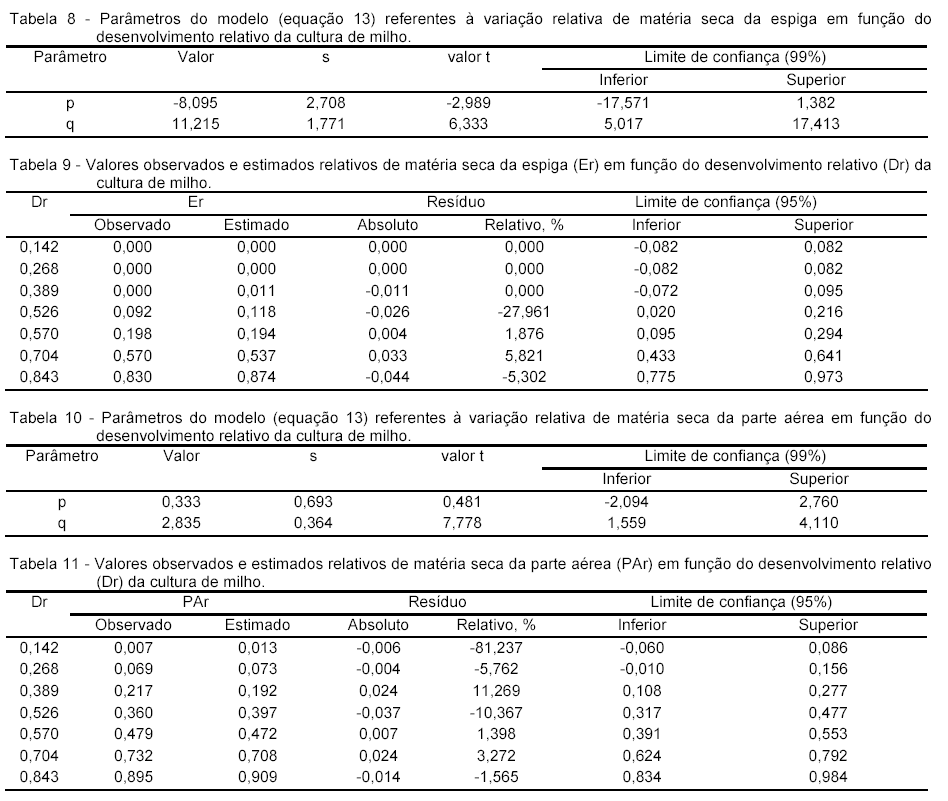
A Figura 2 ilustra a variação dos vários caracteres estudados em função do desenvolvimento relativo (Dr) da cultura de milho, isto é, a magnitude dos desvios (resíduos) entre os valores estimados pelo modelo universal e os observados em função do desenvolvimento relativo da cultura de milho. Para estimativa da matéria seca das diferentes partes da planta de milho, foram concebidos dois modelos (tipo I e tipo II), cujos dados obtidos são apresentados nas Tabelas 2 a 11. O modelo tipo I foi proposto para estimar a matéria seca relativa do colmo, espiga e parte aérea. O modelo tipo II foi utilizado para estimar a matéria seca relativa da folha e do pendão. A matéria seca da parte aérea é calculada pela soma de matéria seca do colmo, folha, pendão e espiga.

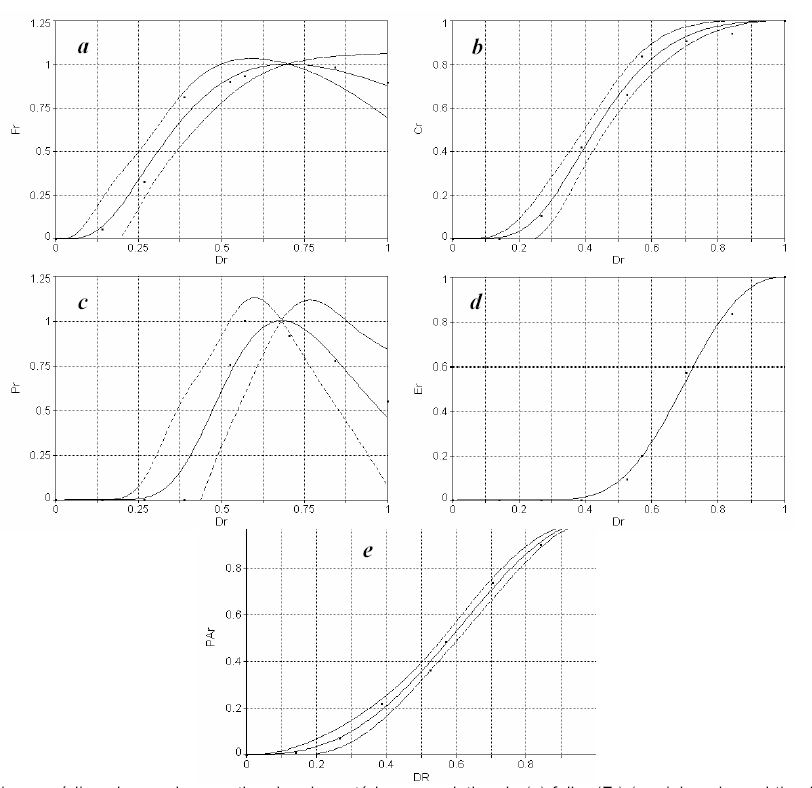
Figura 2 - Valores médios observados e estimados de matéria seca relativa de (a) folha (Fr) (modelo universal tipo II); (b) colmo (Cr) (modelo universal tipo I); (c) pendão (Pr) (modelo universal tipo II); (d) espiga (Er) (modelo universal tipo I) e (e) parte aérea (PAr) (modelo universal tipo I) em função do desenvolvimento relativo (Dr) da cultura de milho. As curvas externas (inferior e superior) ilustram o intervalo de confiança com 99% de probabilidade.

A curva de secagem a campo após o ponto de maturidade fisiológica depende do material genético e das condições climáticas, principalmente. A umidade relativa e a temperatura do ar, bem como a ocorrência de chuva e ventos impossibilitam a obtenção de modelo extrapolável.

A proposição dos modelos são justificáveis por se tratarem de uma importante ferramenta para definição de população de plantas, épocas de semeadura e de colheita, bem como otimizar a utilização de fertilizantes, e definir o momento de corte de milho para silagem, por exemplo. Tais definições racionalizam a produção permitindo maior aproveitamento dos recursos naturais, favorecendo assim o planejamento de atividades ao nível de propriedade e no zoneamento agrícola ao nível de região. Pode-se também, determinar as regiões onde ocorrem o máximo acúmulo de metabólitos e que determinam a época limite de aplicação do nutriente de interesse em cobertura (caso do nitrogênio, por exemplo), o que ocorre próximo ao estádio de doze folhas no caso do milho.

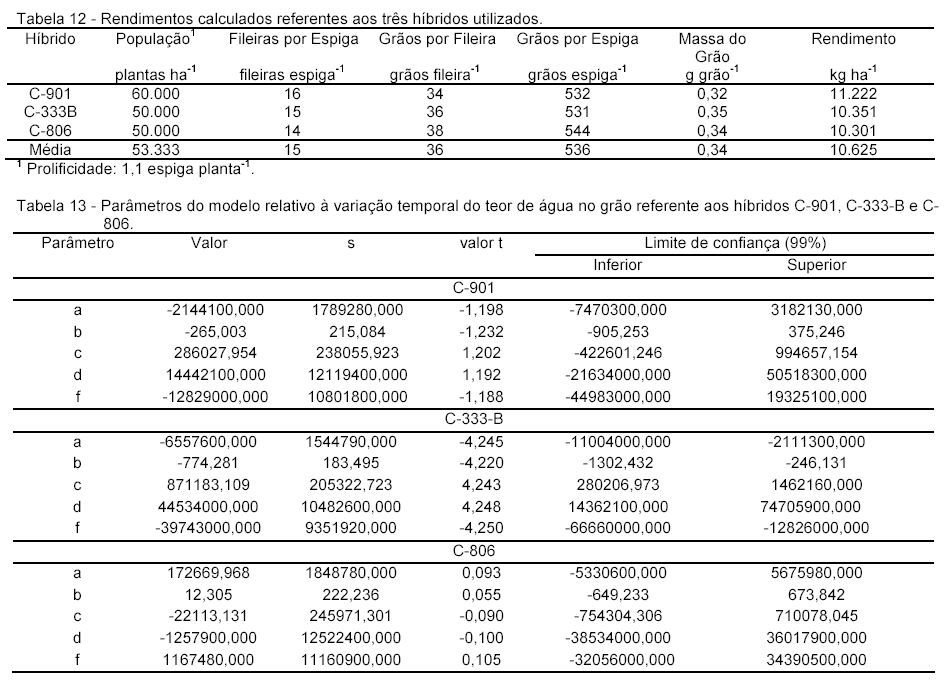
Os resultados obtidos (Tabelas 12 e 13) demonstram que o método proposto é perfeitamente viável e que pode ser utilizado como uma ferramenta para estimar a produtividade de grãos de uma cultura de milho.

Os modelos auxiliam a interpretação de dados experimentais, sendo mais uma ferramenta para o desenvolvimento de técnicas de pesquisa que visem melhor nortear as ações de manejo no ambiente agrícola (WIT, 1982).

É importante a constante busca de procedimentos que organizem melhor a informação existente, que identifiquem as limitações atuais de conhecimento e que viabilizem a extrapolação de resultados minimizando, dentro de certos limites, a necessidade da condução de experimentos de campo.

A definição do fator redutor de produtividade é importante no intuito de estabelecer que toda e qualquer ação de manejo efetuada pelo Homem na escala de cultura, para um determinado material genético numa condição climática específica, é no intuito de minimizar estresse do ambiente.

A produtividade não aumenta com adubação, com controle de plantas daninhas ou com controle de pragas e doenças. O modelo que norteia as referidas ações, leva em consideração o fator econômico. Sendo assim, uma intervenção é recomendável apenas quando o custo da mesma for inferior ao valor monetário da suposta perda de receita bruta, a qual é dependente da perda de produtividade e do preço de mercado esperados. Essa é a utilidade da estimativa de produtividade como uma importante ferramenta (modelagem) para nortear decisões.

Os modelos propostos são precisos na estimativa do acúmulo de matéria seca nos diversos órgãos da parte aérea das plantas de milho, bem como para prever o rendimento de grãos da cultura.

AFUAKWA, J.J.; CROOKSTON, R.K.; JONES, R.J. Effect of temperature and sucrose availability on Kernel black layer development in maize. Crop Science, Madison, v.24, n. 2, p.285-288, 1984.

ANDRADE, F.H. Analysis of growth and yield of maize, sunflower and soybean grown at Balcarce, Argentina. Field Crops Research, Amsterdam, v.41, p.1-12, 1995.

BROWN, D; ROTHERY, P. Models in biology: mathematics, statistics and computing. Baffins Lane: Wiley, 1993. p.1-9.

BARROS, I.Q. Introdução ao cálculo numérico.São Paulo : Edgar Blücher Ltda, 1976.

BARROS, A.H.C. Análise de crescimento, do desenvolvimento e da produtividade da cultura de milho (Zea mays L.): Experimentos e modelos.1998. 85p. Dissertação (Mestrado) – Universidade Federal de Viçosa.

BOOTE, K.J.; JONES, J.W.; PICKERING, N.B. Potential uses and limitations of crop models. Agronomy Journal., Madison, v.88, p.704-716, 1996.

CHEN, S.C.; FONSECA, L.B. Corn yield model for Ribeirão Preto, São Paulo State, Brazil. Agricultural Meteorology, Amsterdam, v. 22, p.341-349, 1980.

FANCELLI, A.L.; DOURADO-NETO, D. Tecnologia da produção de milho. São Paulo :FEALQ/Departamento de Produção Vegetal: ESALQ/USP, 1999.

MIRSHAWKA, V. Cálculo Numérico.São Paulo : Editora Nobel, 1989.

PECHER, A.; HAHN, S. Using tools for modelling and solving agricultural problems under risk. Computer and Electronics in Agriculture, New York, v.22, p.187-197, 1999.

WHISLER, F.D.; ACOCK, B.; BAKER, D.N. Crop simulation models in agronomic systems. Advances in Agronomy, New York, v.40, p.141-208, 1986.

THORNLEY, J. H. M.; JOHNSON, I. R. Plant and crop modelling: a mathematical approach to plant and crop physiology. Oxford: Clarendon Press, 1990. 669p.

WIT, C.T. Simulation of living systems. In: PENNING DE VRIES, F. W.T.; VAN LAAR, H.H (Ed.). Simulation of plant growth and crop production. Wageningen: Pudoc, 1982.p.3-8.