 Página anterior Página anterior |   Voltar ao início do trabalho Voltar ao início do trabalho | Página seguinte  |
A busca pela sistematização do conhecimento fez surgir a chamada Engenharia do Conhecimento. Pode-se dizer é que é a responsável por colher informações necessárias ao desenvolvimento de sistemas inteligentes, utilizando-se de especialistas que irão "emprestar" ou mesmo transferir o conhecimento necessário para as futuras tomadas de decisão do próprio sistema.
Essa transferência tem como premissa que o ser humano enxerga a realidade que o cerca de forma estruturada, ou como menciona PEROTTO (2001:p.02), por meio de "modelos explicativos do mundo":
O ser humano trabalha com a expectativa de que a realidade possua um funcionamento regular, buscando, assim, leis de regularidade e modelos explicativos do mundo. Esses modelos não podem ser logicamente confirmados, mas apenas refutados quando da ocorrência de casos que contradigam o modelo (contra-exemplos) [Popper]. A proposição de modelos e de hipóteses é um processo criativo dos cientistas.
A melhor descrição dos objetivos, como também a aplicabilidade da Engenharia do Conhecimento, talvez seja aquela que diz que:
A EC procura investigar os sistemas baseados em conhecimento e suas aplicações, englobando atividades como: investigação teórica de modelos de representação do conhecimento, estabelecimento de métodos de comparação, tanto do ponto de vista formal como experimental entre os diferentes modelos, desenvolvimento de sistemas baseados em conhecimento e estudo das relações entre sistemas e o processo ensino/aprendizagem 3.
Compreende-se, portanto, a necessidade de escolher formas que possam traduzir esse conhecimento "apreendido" do homem, transferindo-o para um sistema com capacidade de simulação da mente humana. Surge, assim, o que se convencionou denominar de Representação do Conhecimento. Nas palavras de ROCHA FERNANDES (2005:p. 09), a "Representação do Conhecimento pode ser definida como um conjunto de convenções sintáticas e semânticas que tornam possível descrever coisas".
A visão de que há várias unidades interconectadas idênticas que são coletivamente responsáveis para representar vários conceitos é chamada conexionista. Assim, um conceito é representado num senso distribuído e é indicado pelo envolvimento em atividades sobre uma coleção de unidades ROCHA FERNANDES (2005:p. 09). A seguir algumas das características das formas de representação do conhecimento segundo ROCHA FERNANDES:
Vários são os modelos que podem ser utilizados para a representação do conhecimento. Neste trabalho, tomamos como base aqueles citados por ROCHA FERNANDES (2005:p. 09):
Conhecimento procedimental: O conhecimento é representado em forma de funções/procedimentos. O cerne de tal conhecimento consiste em ser capaz de fazer, ou dizendo melhor, de como. Portanto, os procedimentos "são um conjunto de ações organizadas para a consecução de uma meta". Por outro lado, o conhecimento declarativo, consiste apenas em saber o quê.
Redes: Conhecimento representado por um rótulo de grafos direcionados cujos nós representam conceitos e entidades, enquanto os arcos representam a relação entre entidades e conceitos. Redes Semânticas: é a forma de representação mais adequada para domínios onde problemas podem ser descritos como taxonomias, classificações complexas. As redes semânticas são representadas como um conjunto de nós ou nodos que são ligados por meio de arcos, onde cada nodo representa um objeto, uma entidade conceitual ou um evento e cada arco representa o relacionamento existente entre cada par de nodos, sendo que cada par de nodos representa um determinado fato. Na figura 1, cão e gato são ambos instâncias de classes genéricas. Pode-se generalizar também a relação entre eles representando os indivíduos específicos com nodos anônimos e indicando a inclusão deste indivíduo em sua respectiva classe por meio da relação "é um". Os nodos rotulados representam classes genéricas e os nodos anônimos representam indivíduos específicos. Para saber se um nodo representa uma instância é só observar se ele está na origem de algum arco do tipo "é um".
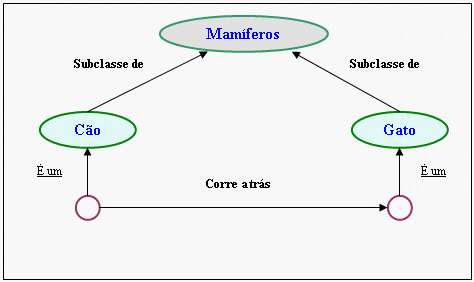
Figura 1. Representação elementar do conhecimento: "O cão corre atrás do gato".
Fonte: SIQUEIRA, 1999.
Lógica: Um modo de declaração que representa o conhecimento uma das mais primitivas formas de representação do raciocínio ou conhecimento humano. A lógica preposicional é considerada a forma mais comum da lógica. Baseia-se em que proposição só pode ter um dos seguintes valores: verdadeira ou falsa. A lógica de predicados é considerada como uma extensão da lógica preposicional. Na lógica de predicados os elementos fundamentais são, além do objeto, também os seus predicados.
Árvores de decisão: Conceitos são organizados em forma de árvores. Elas fazem jus à expressão "dividir para conquistar", ou seja, um problema complexo é decomposto em subproblemas mais simples. A mesma metodologia é aplicada a cada problema seguinte. A figura 2 demonstra esquematicamente esse conceito: cada nó de decisão contem um teste num atributo; cada ramo descendente corresponde a um possível valor deste atributo; cada Folha está associada a uma classe; cada percurso na arvore (da raiz à folha) corresponde a uma regra de classificação. No espaço definido pelos atributos, cada folha corresponde a uma região (Hiper-retângulo); a intersecção dos hiper-retângulos é vazia e a união dos hiper-retângulos é o espaço completo.
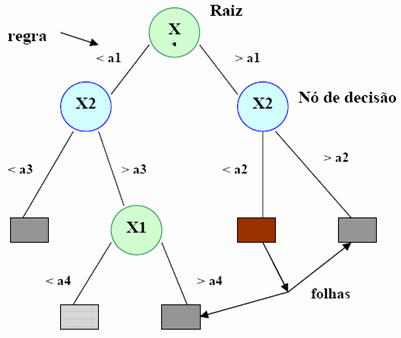
Figura 2. Árvores de decisão.
Fonte: GAMA (2002: p. 05).
Conhecimento estatístico: Como o próprio nome diz, o conhecimento estático agrupa todo o conhecimento que não varia. O uso de fatores de certeza, Bayesain, Redes, Dempster-Shafer theory, Lógica Fuzzy.
Regras: O uso de sistemas de Produção para codificar regras de condição-ação. Consiste em representar o domínio do conhecimento através de um conjunto de regras. Suas principais características são: modularidade, facilidade de implantação e também a grande quantidade de pacotes desta técnica existente para o desenvolvimento de Sistemas Especialistas. É a mais conhecida forma de representar conhecimento, usada atualmente apenas em sistemas de pequeno porte.
Processamento paralelo distribuído: Utiliza-se de modelos conexionistas. Seu principal objetivo é o aumento do desempenho de aplicações que necessitam de grande poder computacional e que são pouco eficientes quando executadas de forma seqüencial. Esse aumento de desempenho é conseguido fazendo a partição de uma tarefa em tarefas menores e executando-as em diferentes processadores de forma paralela.
Esquemas híbridos: Qualquer representação do formalismo que emprega a combinação de esquemas de representação do conhecimento.
Frames: muito parecidas com a rede semântica, exceto que cada nó representa conceitos e/ou situações. Cada nó tem várias propriedades que podem ser especificadas ou herdadas por padrão. O modelo "frames" para a representação do conhecimento foi introduzido inicialmente em 1975 por Marvin Minsky. Em geral, um frame é uma coleção de atributos, chamados de slots, e valores, que descrevem alguma entidade do mundo (RICH & KNIGHT, 1993). Os "frames" integram conhecimento declarativo sobre objetos e eventos e conhecimento procedimental sobre como recuperar informações ou calcular valores. Os atributos também apresentam propriedades, que dizem respeito ao tipo de valores e às restrições de numero que podem ser associadas a cada atributo. Essas propriedades recebem o nome de facetas. Assim como nas redes semânticas, uma das características dos "frames" é a possibilidade de que sejam criados novos subtipos de objetos que herdem todas as propriedades da classe original.
Casos: usa experiência passada, acumulando casos e tentando descobrir, por comparação, soluções para outros problemas.
"... a matéria da qual somos feitos veio das estrelas quando estavam morrendo e um dia nossa matéria vai fazer parte de outras estrelas que estarão nascendo. [ ..]. um dia nossa matéria vai se espalhar pelo Universo e, quem sabe, voltar a gerar outros planetas e até outras formas de vida" – Marcelo Gleiser.
Tomando como base os modelos propostos por GANASCIA (1993) e reproduzidos por ROCHA FERNANDES (2005:p. 04), os principais modelos de IA são: Algoritmo Genético, Programação Evolutiva, Lógica Fuzzy, Sistemas baseados em Conhecimento, Raciocínio Baseado em Casos, Programação Genética e Redes Neurais. Tais modelos serão detalhados neste Capítulo.
3.1- Algoritmos Genéticos
É um modelo para o aprendizado da máquina, inspirado no livro Origem das Espécies, através da Seleção Natural, escrito pelo naturalista inglês Charles Darwin (1809-1882), criador da teoria evolucionista, segundo a qual somente os mais adaptados ao meio sobrevivem.
Os algoritmos genéticos foram criados por Jonh Holland (1975), objetivando emular operadores genéticos (específicos, como crossing-over, mutação e reprodução) da mesma forma como é observado na natureza, ou seja, pretendia simular matematicamente todo o mecanismo da evolução biológica, com todas as características e vantagens desse processo.
O processo envolve a criação, dentro da máquina, de uma população de indivíduos representados por cromossomos. Os indivíduos passam por um processo simulado de evolução, seleção e reprodução, gerando uma nova população.
Segundo BARBOSA e FREITAS (2006):
Os algoritmos evolutivos (AEs) se caracterizam, principalmente, pela priorização da tratabilidade do problema ao invés da busca pela solução ótima. Eles se auto-organizam e se adaptam em busca de uma solução que resolva o problema em questão. Nos AE’s, funções são definidas para se obter novos indivíduos e selecionar os que comporão a nova geração de sua população. Antes de se fazer a seleção, operações de permuta (crossover) e mutação são realizadas sobre os indivíduos realizando o cruzamento entre eles.
Ainda segundo BARBOSA e FREITAS (2006), pode-se definir formalmente um AG da seguinte forma:
AG = (N, P, F, ), onde:
P: população de N indivíduos, P = {S1, S2, ..., SN}. Si, representa cada indivíduo variando entre i=1, .., N, ou seja, Si é um conjunto de possíveis soluções para o problema.
F: representa a função objetivo (fitness), retornando um valor positivo e real na avaliação de cada indivíduo. F: Si R+ , i = 1, .., N
: operador de seleção de r pais para o cruzamento. : P {p1, p2, ..., pr}
: conjunto de operadores: C (crossover) e M (mutação) e outros possíveis
operadores que produzem s filhos a partir de r pais.
= {c, M, ...}: {p1, p2, ..., pr} {f1, f2, ..., fs}
: operador de remoção que retira s indivíduos selecionados da geração Pt e, por exemplo, permite acrescentar s filhos a partir de r pais na nova geração Pt+1 .
Pt+1 = Pt – (Pt ) + {f1, f2, ..., fs}
Partindo da correlação anteriormente citada, relativa a cromossomos, é dito que ao seu conjunto se dá o nome de "população" (BERKENBROCK e ROJAS). Segundo os autores citados é preciso considerar também dentro da população:
O seu tamanho, pois ele afeta o desempenho global e a eficiência dos AG's. Uma população muito pequena oferece uma pequena cobertura do espaço de busca, causando uma queda no desempenho. Uma população suficientemente grande fornece uma melhor cobertura do domínio do problema e previne a convergência prematura para soluções locais. Entretanto, com uma grande população tornam-se necessários recursos computacionais maiores, ou um tempo maior de processamento do problema.
Assim, tem-se um cromossomo como uma estrutura de dados, geralmente vetor ou cadeia de bits, que representa uma possível solução do problema.
Como na natureza, em que a combinação das características genéticas dos mais fortes dá lugar a indivíduos mais adaptados ao meio, também aqui existe um processo de seleção, que visa escolher cromossomos em uma população para a reprodução. "A fase de seleção descarta os cromossomos com baixa aptidão, desta forma, muitos genes mutados durante a evolução são eliminados" (BERKENBROCK e ROJAS).
Com base na obra de BERKENBROCK e ROJAS, serão mencionados, a seguir, alguns conceitos chave para a compreensão do processo de formação dos AGs.
3.1.2- Seleção
O processo de seleção pode ocorrer das seguintes formas:
3.1.3- Recombinação
A recombinação é um dos principais mecanismos de busca dos AG's para explorar regiões desconhecidas do espaço de busca. O operador é simples e visa realizar a troca de sub-partes entre dois cromossomos. Neste processo, um par de cromossomos pai gera dois cromossomos filhos. Cada um dos cromossomos pais tem sua cadeia cortada em uma posição, e suas sub-partes são trocadas entre si. A recombinação é aplicada com uma dada probabilidade a cada par de cromossomos selecionados.
3.1.4- Mutação
A mutação é outro mecanismo principal de busca dos AG's para explorar regiões desconhecidas do espaço de busca. O processo consiste na troca aleatória dos valores da "string" de um cromossomo. Assim como na natureza, a probabilidade de vir a acontecer mutação genética é muito pequena. Nos AG's, a mutação pode ocorrer em qualquer posição na cadeia de "strings". A mutação melhora a diversidade dos cromossomos da população inicial, em contra partida, destrói informações contidas no cromossomo. Em resumo, a mutação reflete uma taxa de alteração de um gene 0 em 1 ou vice-versa.
3.2- Programação Evolutiva
Campo da IA concebido por Lawrence J. Fogel (1960), assemelha-se aos algoritmos genéticos, sendo que é dada maior ênfase na relação comportamental entre os parentes e seus descendentes. As soluções para os problemas são obtidas por meio tentativas e transmitidas para a nova população (simulada em programas).
3.3- Lógica Fuzzy
Também denominada de Conjuntos Difusos ou Lógica Nebulosa. Foi estruturada por Lofti Zadeh da University of Califórnia, no ano de 1965.
Se considerarmos a lógica de Aristóteles (384 - 322 a.C.), que foi o responsável pelo estabelecimento de um conjunto de regras rígidas para que conclusões pudessem ser aceitas logicamente válidas, verificamos que a lógica ocidental caracterizou-se, desde então, por ser binária. Sua lógica se baseava em premissas e conclusões. Consideremos o seguinte silogismo: se é constatado que "todo ser vivo é mortal" (premissa 1); e observa-se que "Sócrates é um ser vivo" (premissa 2), tem-se como única conclusão possível: "Sócrates é mortal". Assim, verificamos que uma declaração é falsa ou verdadeira, nunca podendo ser num mesmo instante parcialmente verdadeira e parcialmente falsa.
As primeiras noções da lógica4 dos conceitos "vagos" foi desenvolvida por um lógico polonês Jan Lukasiewicz (1878-1956) em 1920 que introduziu conjuntos com graus de pertinência sendo "0, ½ e 1" e, mais tarde, expandiu para um número infinito de valores entre 0 e 1.
Consta que a primeira publicação sobre lógica "fuzzy" data de 1965, quando então recebeu este nome. Seu autor, como dito anteriormente, foi Lotfi Asker Zadeh, professor em Berkeley, Universidade da California. Zadeh criou a lógica "fuzzy" combinando os conceitos da lógica clássica e os conjuntos de Lukasiewicz, definindo graus de pertinência.
A Lógica Difusa (Fuzzy Logic) insere o conceito de dualidade, estabelecendo que algo possa e deve coexistir com o seu oposto. Ao tomarmos com base o ser humano, e suas inevitáveis incertezas, podemos entender que a lógica Aristotélica não pode ser aplicada indistintamente, reduzindo-a a simples classificação de verdadeiro ou falso.
Um exemplo simples de Lógica Fuzzy pode ser encontrado no artigo publicado por SILVEIRA, demonstrando a diferença entre a computação clássica e aquela que se utiliza da Lógica Difusa:
a) Conceito de alto e baixo na computação clássica
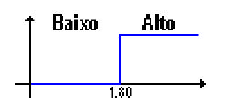
Figura 3.
b) Conceito de alto na lógica fuzzy
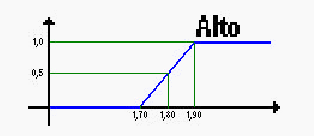
Figura 4.
No conceito clássico, uma pessoa com 1,79 m é considerada tão baixa como uma pessoa de 1,00 m. Por outro lado, uma pessoa com 1 cm a mais (1,80 m) seria considerada tão alta quanto uma pessoa de 2,00 m. Na lógica fuzzy, pensamos em alto da seguinte maneira: alguém com 1,65 m pode ser considerada alto? Nunca. A partir de 1,70 m, podemos começar a pensar que o indivíduo é alto. Para isto, atribuímos um grau de certeza, conforme a altura aumenta. Este grau é chamado de grau de pertinência e varia de 0 a 1. Marcamos então, a fronteira da negação total, ou 0, e da aprovação total, ou 1. De acordo com o gráfico apresentado no conceito de lógica fuzzy, os limites para negação total é de 1,70 m e para aprovação total é de 1,90 m. Isto quer dizer que se o indivíduo medir 1,70 m, com certeza não é alto, enquanto que, se medir 1,90 m, com certeza é alto. Valores abaixo de 1,70 m garantiriam que o indivíduo não é alto, enquanto que valores acima de 1,90 m garantiriam que o indivíduo é alto. Para os valores intermediários, o indivíduo seria considerado alto, mas com um grau de pertinência inferior a 1. Para 1,80 m, o indivíduo seria considerado alto, com grau de pertinência igual a 0,5 (SILVEIRA).
Devido ao desenvolvimento e as inúmeras possibilidades práticas dos sistemas fuzzy e o grande sucesso comercial de suas aplicações, a lógica fuzzy é considerada uma técnica de ampla aceitação na área de controle de processos industriais.
3.4- Sistemas Baseados em Conhecimento
Verificou-se que os métodos inicialmente desenvolvidos em Inteligência Artificial para a solução de problemas, bem como técnicas de buscas, não eram suficientes para resolver os diversos problemas orientados às aplicações.
Como diz BARBALHO (2001:p. 02):
A essência desses sistemas é a aquisição de uma base de conhecimento heurístico, geralmente representada através de um conjunto de expressões condicionais qualitativas e com significado verbal, cujo mérito é serem semanticamente claras. Esses sistemas são capazes de ampliar sua base de conhecimento definida inicialmente, através de um processo de inferência ou "aprendizado" e são, por isso, às vezes, chamados de sistemas inteligentes.
Assim, certos problemas difíceis somente poderiam ser resolvidos com a ajuda de um conhecimento dito específico sobre o domínio desse mesmo problema.
À vezes, o SBC está interligado com a utilização da lógica difusa, ou como diz BARBALHO (2001:p. 02):
A motivação para a construção desses sistemas ‘casados’ foi combinar o rigor empírico das técnicas tradicionais com a interpretabilidade das descrições da Inteligência Artificial para tratar problemas complexos da vida real.
O fruto desse "casamento" é justamente a melhora no aprendizado desses sistemas, pois, como diz BARBALHO (2001:p. 02), a melhora é significativa "quando se dispõe de um conhecimento especialista, na forma de um conjunto de regras a serem melhoradas empiricamente".
Em resumo, SBC são sistemas que implementam comportamentos inteligentes de especialistas humanos.
3.5- Raciocínio Baseado em Casos
É o campo de estudo da IA que utiliza uma grande biblioteca de casos para consulta e resolução de problemas. Os problemas atuais são resolvidos, através da recuperação e consulta de casos já solucionados e da conseqüente adaptação das soluções encontradas. Por exemplo, o Sistema CASEY, que faz o diagnóstico em pacientes cardíacos baseado na consulta de arquivos de pacientes com o mesmo diagnóstico.
No entanto, a mais clara e simples definição do que seja RBC encontra-se na Enciclopédia Virtual Wikipedia: "é o processo de resolver novos problemas tomando como base soluções de problemas similares já superados". A experiência leva à resolução de problemas por similaridade.
O RBC costuma ser formalizado como um processo composto por quatro partes (Enciclopéida Wikipedia), como exemplificado a seguir:
3.6- Programação Genética
"É um campo de estudo da IA voltado para a construção de programas que visam imitar o processo natural da genética. Trabalha com métodos de busca aleatória" (ROCHA FERNANDES, 2005:p. 04).
Segundo RUSSELL e NORVIG (2004:p. 130), embora exista estreita relação entre programação genética e algoritmo genético,
A principal diferença é que as representações que sofrem mutações e combinações são programas, em vez de cadeias de ‘bits’. Os programas são representados sob a foram de árvores de expressões; sendo que estas podem estar em uma linguagem padrão como LISP ou podem ser projetadas especificamente para representar circuitos, controladores de robôs, por exemplo.
A Programação Genética manipula soluções corretas e incorretas, encoraja inconsistências e abordagens contraditórias, não apresenta uma variabilidade dinâmica lógica, é predominantemente probabilística, produz soluções não-parcimoniosas e não apresenta um critério de terminação claramente definido.
A programação genética não usa o operador mutação e a recombinação se dá pela troca de sub-árvores entre dois indivíduos candidatos à solução do problema.
A implementação de uma PG é conceitualmente imediata quando está associada a linguagens de programação que permitem a manipulação de um programa computacional na forma de uma estrutura de dados, inclusive por possibilitar que novos dados do mesmo tipo e recém criados sejam imediatamente executados como programas computacionais.
3.7- Redes Neurais Artificiais (RNA)
Os neurônios são células cerebrais que têm papel fundamental no funcionamento tanto do corpo como do raciocínio humanos. Sua estrutura básica é formada por dendritos, que podem ser compreendidos como um conjunto de terminais de entrada (input), pelo corpo central (processamento), e pelos axônios que são longos terminais de saída (Figura 3).

Figura 5 – Esquema de célula nervosa
Fonte: baseado em RUSSELL e NORVIG (2004:p. 13).
Segundo ALECRIM (2004):
A rede neural se assemelha ao cérebro em dois pontos: o conhecimento é obtido através de etapas de aprendizagem e pesos sinápticos são usados para armazenar o conhecimento. Uma sinapse é o nome dado à conexão existente entre neurônios. Nas conexões são atribuídos valores, que são chamados de pesos sinápticos. Isso deixa claro que as redes neurais artificiais têm em sua constituição uma série de neurônios artificiais (ou virtuais) que serão conectados entre si, formando uma rede de elementos de processamento.
Foi essa estrutura nervosa – também conhecida pelos nomes de conexionismo, processamento distribuído paralelo e computação neural – que serviu de modelo para o processamento criado por McCullock e Pitts (ROCHA FERNANDES, 2005:p. 60), que consiste:
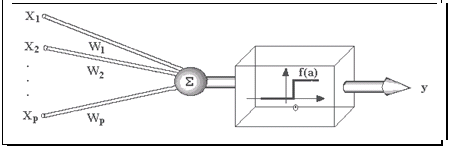
Figura 6 - Esquema da Unidade de McCullock e Pitts –
Fonte: Rocha Fernandes (2005:p. 60)
Supondo existirem "p" sinais de entrada "X1, X2, ..., Xp" e pesos "w1, w2, ..., wp" e um limitador "t"; com sinais assumindo valores booleanos (0 ou 1) e pesos em valores reais.
Neste modelo, o nível de atividade "a" é dado por:
a = w1X1 + w2X2 + ... + wpXp
A saída y é dada por
y = 1, se a >= t ou
y = 0, se a < t.
A organização básica das RNA (Figura 5) é a disposição em camadas, com unidades que podem estar conectadas às unidades da camada posterior (ROCHA FERNANDES – 2005:p. 61).
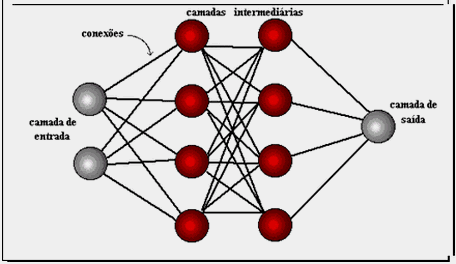
Figura 7 – Camadas de uma RNA
Fonte: ROCHA FERNANDES (2005:p. 61).
De acordo com RUSSELL e NORVIG (2004:p. 715) existem duas categorias principais de estruturas de RNA:
3.6.1- Aprendizado
Até aqui foi demonstrada a forma como se processa a informação pelas RNA, mas seguindo seu modelo humano, resta um fator fundamental que é a aprendizagem. Pode-se dizer que um algoritmo de aprendizado é um "conjunto de regras bem definidas para a solução de um problema de aprendizado" (ROCHA FERNANDES – 2005:p. 63), ou conforme disse EMERSON ALECRIM (2004):
O processo de aprendizagem das redes neurais é realizado quando ocorrem várias modificações significantes nas sinapses dos neurônios. Essas mudanças ocorrem de acordo com a ativação dos neurônios. Se determinadas conexões são mais usadas, estas são reforçadas enquanto que as demais são enfraquecidas. É por isso que quando uma rede neural artificial é implantada para uma determinada aplicação, é necessário um tempo para que esta seja treinada.
Ainda segundo ROCHA FERNANDES (2005:p. 63) existem três formas de aprendizagem:
3.6.2- Aplicações para redes neurais
Um dos vários exemplos de utilização das RNA são os softwares de reconhecimento de voz, pois precisam aprender a conhecer a voz de determinadas pessoas. Há, ainda, o uso em equipamentos robóticos para desarme de bombas. Uma outra aplicação mais ao alcance do público são os chamados softwares OCR que servem para digitalizar textos, por exemplo, e que precisam aprender a reconhecer caracteres da imagem. Também existem programas para controle de acesso por reconhecimento de impressão digital, como, por exemplo, o protótipo desenvolvido por ALEXSANDRA ZAPAROLI, Bacharelanda da Universidade Regional de Blumenau-SC. Contudo, as redes neurais são usadas principalmente em aplicações complexas, como usinas, mercado financeiro e etc.
"... cada passo que se faz em direção ao conhecimento mais intimo da natureza, conduz à entrada de novos labirintos..." - Alexandre de Humboldt.
A parcela essencial no desenvolvimento de estruturas de IA está destinada à formalização dos meios necessários que possam representar e identificar, para a máquina, os meandros do pensamento humano ou, nas palavras de ROCHA FERNANDES (2005:p. 08):
A manifestação inteligente pressupõe aquisição, armazenamento e inferência de conhecimento. Para que o conhecimento possa ser armazenado, é essencial que se possa representá-lo.
Complementando as informações já apresentadas no Capítulo sobre Engenharia do Conhecimento, serão apresentados de forma resumida os dois principais processos lógicos no desenvolvimento da representação do conhecimento humano: a Lógica Proposicional e a Lógica de Primeira Ordem. E ainda com o objetivo de melhor explicar, será também reproduzido, de forma contrita, o exemplo da lógica de primeira ordem apresentado por RUSSELL e NORVIG, na obra "Inteligência Artificial", salientando as noções mais relevantes para sua construção.
4.1- Lógica Proposicional
Embora não seja objeto principal do presente trabalho o aprofundamento em lógica de programação, houve necessidade de pesquisar e, portanto, apresentar algumas noções de lógica proposicional, ou booleana, visando uma melhor compreensão da lógica de primeira ordem, esta sim usada em IA.
A Lógica Proposicional é um sistema formal apropriado para a representação de teorias simples, ou seja, aquelas compostas de proposições elementares (proposições que não envolvem quantificadores e variáveis).
Segundo TERRA (2006), a linguagem proposicional possui três características principais:
O alfabeto da Linguagem Proposicional é composto dos seguintes símbolos conectivos:
Seguindo os exemplos postulados por HERNANDEZ (2000), serão detalhados, embora de forma compacta, os respectivos conectivos e suas Tabelas Verdade:
4.1.1- Conectivo "e"
Se p e q são duas proposições então "p e q" é também uma proposição. Pode-se dizer que:
De acordo com o esquema de representação adotado acima, dizemos que:
então p q é verdadeira
senão p q é falsa.
De acordo com a proposição anterior, o significado de p q pode ser expresso através da seguinte tabela verdade:
|
P |
q |
p q |
|
V |
V |
V |
|
V |
F |
F |
|
F |
V |
F |
|
F |
F |
F |
4.1.2- Conectivo "ou"
Se p e q são duas proposições então "p ou q" é também uma proposição. Pode-se dizer que:
De acordo com o esquema de representação adotado acima, dizemos que:
então p q é verdadeira
senão p q é falsa.
O significado de p q pode ser expresso através da seguinte tabela verdade":
|
P |
q |
p q |
|
V |
V |
V |
|
V |
F |
V |
|
F |
V |
V |
|
F |
F |
F |
A disjunção aqui é chamada ‘ou inclusivo’, ou seja, corresponde ao e/ou algumas vezes encontrada em documentos legais. Neste caso, conforme pode ser observado na tabela verdade acima, a proposição composta é verdadeira, inclusive, quando ambas sub-proposições envolvidas são verdadeiras.
É preciso destacar, também, o ou no sentido exclusivo, que normalmente ocorre na linguagem comum. Por exemplo:
Neste caso, a verdade desta proposição não inclui as duas sub-proposições, ou seja, a proposição composta é verdadeira quando exatamente uma das sub-proposições é verdadeira.
Considerando a observação anterior, pode-se utilizar a seguinte tabela verdade para definir o ‘ou-exclusivo’:
|
P |
q |
P q |
|
F |
F |
F |
|
F |
V |
V |
|
V |
F |
V |
|
V |
V |
F |
4.1.3- Conectivo "não"
Se p é uma proposição então "não p" é também uma proposição. Pode-se dizer que:
De acordo com o esquema de representação anterior, dizemos que:
então p é falsa
senão p é verdadeira.
O significado de p pode ser expresso através da seguinte tabela verdade:
|
p |
p |
|
F |
V |
|
V |
F |
4.1.4- Implicação
Se p, q são proposições então "se p então q" é também uma proposição, pode-se dizer que:
Nesta proposição, p é denominada premissa (ou hipótese) e q é denominada conclusão (ou conseqüência ou conseqüente).
De acordo com o esquema de representação citado anteriormente, pode-se dizer que:
então p q é falsa
senão p q é verdadeira.
O Significado de p q pode ser expresso através da seguinte tabela verdade:
|
P |
q |
p q |
|
V |
V |
V |
|
V |
F |
F |
|
F |
V |
V |
|
F |
F |
V |
4.1.5- Bi-condicional
Se p, q são proposições então "p se e somente se q" (algumas vezes abreviado sss) é também uma proposição. Podemos dizer que:
De acordo com o esquema de representação adotado acima, dizemos que:
então p q é verdadeira
senão p q é falsa.
O significado de pq pode ser expresso através da seguinte tabela verdade":
|
P |
q |
p q |
|
F |
AF |
V |
|
F |
V |
F |
|
V |
F |
F |
|
V |
V |
V |
4.2- Lógica de Primeira Ordem
Enquanto o modelo proposicional é considerado "simplesmente conjuntos de valores-verdade para os símbolos de proposições" (RUSSELL e NORVIG – 2004:p. 237), já os Modelos de Lógica de Primeira Ordem possuem objetos, cujo "domínio de um modelo é o conjunto de objetos que ele contém" (RUSSELL e NORVIG – 2004:p. 237).
4.2.1 – Exemplificação do modelo de primeira ordem
A Figura 8 ilustra um modelo de 5 (cinco) objetos: Ricardo Coração de Leão; rei João; as pernas esquerdas de Ricardo e João; uma coroa.
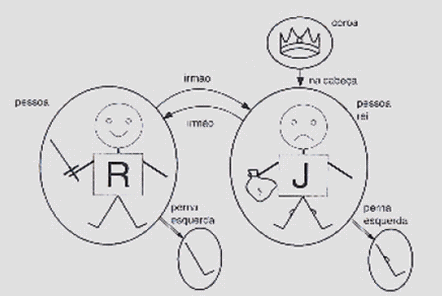
Figura 8 – Modelo contendo cinco objetos, duas relações binárias, três relações unitárias
(indicadas por círculos nos objetos) e uma função unária, perna esquerda.
Fonte: RUSSELL e NORVIG (2004:p. 237).
As relações entre os objetos podem ser variadas, como, por exemplo, o fato de Ricardo e João serem irmãos. Tecnicamente falando, uma relação é um conjunto de tuplas de objetos inter-relacionados, sendo representado por colchetes angulares entre os objetos. Desse modo, a relação entre ambos seria o conjunto:
{ < Ricardo , Rei João > , < Rei João, Ricardo > }
O modelo também possui relações unárias ou propriedades: a propriedade "pessoa" é verdadeira tanto para Ricardo quanto para João.
Talvez a melhor forma de imaginar os tipos de relacionamento seja visualizando funções. Como exemplo, temos: se cada pessoa tem uma perna esquerda, então o modelo tem funções unárias "perna esquerda", que podem ser assim visualizadas:
< Ricardo > Perna esquerda de Ricardo
< Rei João > perna esquerda de João
Os elementos sintáticos básicos da linguagem de primeira ordem são três: Símbolos de Constantes, que representam os objetos; Símbolos de Predicados, que representam as relações, e Símbolos de Funções que representam as próprias funções. Transpondo essas definições para o exemplo ora considerado temos:
- Ricardo e João = símbolos de constante;
- Irmão, NaCabeça, Pessoa, Rei e Coroa = símbolos de predicados;
- PernaEsquerda = símbolos de função;
Outra construção importante é o uso de um termo que se refira a um objeto. Assim, ao invés de atribuir um nome distinto para cada símbolo constante. Por exemplo, em linguagem natural é perfeitamente possível usara a expressão "perna esquerda do rei João", sem, contudo, denomina-la. Essa é justamente a função dos símbolos de funções, pois ao invés de usar um símbolo de constante, pode-se utilizar PernaEsquerda (João).
A reunião de termos referenciando objetos e símbolos de predicado referenciando as relações forma a chamada sentença atômica. Uma sentença atômica é formada a partir de um símbolo de predicado, seguido por uma lista de termos entre parênteses: Irmão (Ricardo, João). O que significa dizer que Ricardo e João são irmãos. Outros termos mais complexos podem advir na construção de sentenças: Casado (Pai (Ricardo), Mãe (João)), o que equivale a dizer que o pai de Ricardo é casado com a mãe de João.
Da mesma forma, podem-se usar conectivos lógicos para criar sentenças mais complexas, como é usado no cálculo proposicional. As sentenças a seguir são verdadeiras para o exemplo da Figura 8.
¬ Irmão (PernaEsquerda (Ricardo), João) = não são irmãos a perna
esquerda de Ricardo e João;
Irmão (Ricardo, João ) ^ Irmão (João, Ricardo) = o mesmo que dizer
que Ricardo e João são irmãos e João e Ricardo são irmãos;
Rei (Ricardo) V Rei (João) = Ricardo é Rei ou João é Rei;
¬ Rei (Ricardo) Rei (João) = o mesmo que dizer que não sendo
Ricardo Rei, implica em que João seja Rei;
4.2.2- Quantificadores
Citando FERREIRA (2001:p. 10):
Se, numa dada condição p(x), atribuirmos à variável x um dos valores do seu domínio, obteremos uma proposição. Outra forma extremamente importante em Matemática de obter proposições a partir de uma condição p(x) é antepor-lhe um dos símbolos ∀x ou ∃x.
"Universal : ∀x (Lê-se: Todo x ou Para todo x ou Qualquer que seja x )
Exemplo: ( ∀x ) ( x + 1 = 7 ), que se lê: "Para qualquer valor de x, x + 1 = 7" ( proposição falsa ).
Existencial : ∃x ( Lê-se: Existe pelo menos um x tal que, ou Existe algum x )
Exemplo: ( ∃x ); ( x + 1 = 7 ), que se lê: "Existe algum x tal que x + 1 = 7" ( proposição verdadeira ).
Existencial Particular : ∃! x ( Lê-se: Existe um único x tal que )
Exemplo: ( ∃! x ); ( x + 1 = 7 ), que se lê: "Existe apenas um x tal que x + 1 = 7" ( que é uma proposição verdadeira ).
Transpondo essas definições para o nosso exemplo (Figura 8), pode-se construir a seguinte sentença: ∀x Rei(x) Pessoa (x), o que equivale a dizer "para todo x, sendo x Rei, implica em que x seja uma pessoa".
Uma forma de dizer que o Rei João tem uma coroa em sua cabeça seria utilizando um quantificador existencial (∃). Assim, a frase seria escrita:
∃x Coroa (x) ^ NaCabeça (x, João) = o que equivale a dizer que existe um x,
tal que x seja uma coroa e a coroa está na cabeça de
João;
4.3- Base do Conhecimento
Indiscutivelmente, a Base do Conhecimento - BC desempenha papel essencial em qualquer sistema que se utiliza de agentes baseados em conhecimento. Tal base é representada por um conjunto de sentenças que, conforme salientam RUSSELL e NORVIG (2004:p. 191) não deve ser confundido com sentenças gramaticais, pois são, na verdade, expressões técnicas reproduzidas em linguagem de representação do conhecimento.
Os nomes para realizar a inserção de sentenças à BC e para efetuar consultas, convencionou-se chamar de: TEEL (informe) e ASK (pergunte).
Segundo RUSSELL e NORVIG (2004:p. 245) as duas sentenças implicam em inferência, pois podem resultar em novas sentenças derivadas de outras mais antigas. Assim, continuando com o exemplo da Figura 8, podemos propor as seguintes sentenças:
TELL (BC, Rei(João)) = equivale a informar à BC que João é um rei;
TELL (BC, ∀ x Rei(x) Pessoa(x)) = equivale a informar à BC que para
todo x que é Rei, implica que todo x é uma pessoa.
Da mesma forma, é possível realizar consultas à BC como nos exemplos a seguir:
ASK (BC, Pessoa(João)) = pergunte à BC se João é uma pessoa. A
resposta, partindo do pressuposto que a BC já é
detentora dessa informação, retorna como
verdadeira a resposta.
A partir das definições precedentes, é possível efetuar a construção de inúmeras sentenças que irão compor a base do conhecimento. Como dito anteriormente, não é pretensão deste trabalho abordar a fundo as linguagens de Representação do Conhecimento, mas tornou-se importante realizar o que se poderia chamar de "parênteses" com vistas a trazer alguns conceitos importantes de como se realiza a transposição da linguagem natural para estruturas compreendidas pela máquina.
4.4- Técnicas de Busca
Segundo ROCHA FERNANDES (2005:p. 07) a heurística é:
Um procedimento para resolver problemas por meio de um enfoque intuitivo, em geral racional, no qual a estrutura do problema passa a ser interpretada e explorada inteligentemente para obter uma solução razoável. São, portanto, métodos ou princípios para decidir, entre vários cursos de ação alternativos, aquele que parecer mais efetivo para atingir um determinado objetivo.
As técnicas de busca heurística podem ser assim classificadas:
a) Busca em Largura: também recebe o nome de busca em amplitude. "Todos os nós de certo nível da árvore são examinados antes do nível abaixo, caso exista uma solução, e se o grafo é finito, a solução será encontrada" ROCHA FERNANDES (2005:p. 07). Em outras palavras, tem como objetivo verificar primeiro os nós mais próximos do nó inicial de um grafo, até chegar ao destino da busca, sendo, por conseqüência, o oposto da busca em profundidade. Entretanto, segundo ROCHA FERNANDES (2005:p. 07) "existem inconvenientes no uso dessa técnica, já que requer muita memória para ser executado, além de exigir um esforço computacional excessivo se o comprimento dos caminhos não for pequeno".
Como exemplo, temos a Figura 9 que representa um mapa de um jogo. Suponhamos que uma pessoa esteja restrita em não caminhar nas coordenadas diagonais, ou seja, como ela se encontra na coordenada (2,2), apenas poderá caminhar nas coordenadas (1,2), (2,1), (2,3) e (3,2). Portanto, o objetivo é chegar na coordenada (3,3). Por meio do método de busca em amplitude ajudará a pessoa a encontrar um caminho que levará ao destino, na figura 8 temos um grafo representando a leitura de busca para esta situação:
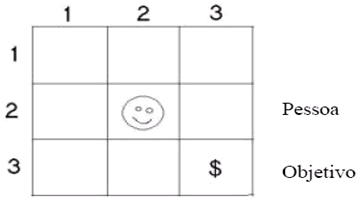
Figura 9 – Espaço de Busca em amplitude.
Fonte: Projeto de Pesquisa em Algoritmos de Busca Aplicados a Motores de Jogos.
Observa-se na Figura 10 que os números de 1 a 11 mostram a seqüência de nós visitados, e cada nó representa uma coordenada da Figura 9. O último nó visitado pela busca foi o 11, que é justamente a coordenada destino da pessoa (3,3). Encontrado o destino, termina-se a busca aplicando o melhor caminho, neste caso é um caminho único que são as coordenadas (2,2), (2,3) e (3,3). Apesar de existir outro caminho, como na coordenada (2,2), (3,2) e (3,3), não foi explorado porque antecipadamente a este caminho já houve o encontrado de um outro.
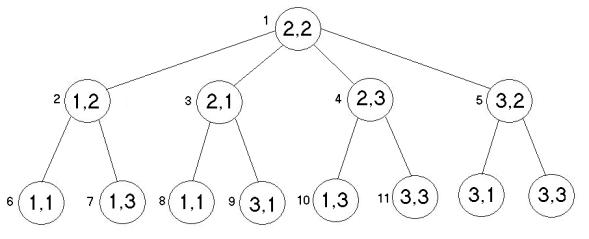
Figura 10 - Árvore de busca de amplitude
Fonte: Projeto de Pesquisa em Algoritmos de Busca Aplicados a Motores de Jogos.
 Página anterior Página anterior |   Voltar ao início do trabalho Voltar ao início do trabalho | Página seguinte  |
|
|
|