Métodos

O modelo matemático

Os dados utilizados neste trabalho foram gerados por simulação em computador, em conformidade com o seguinte modelo:

em que:

y_ijk: é a observação gerada para a parcela do bloco j que recebeu o tratamento (genótipo) i oriundo do cruzamento k;

m: é a constante comum a todas as observações (a média geral, sob restrições do tipo "soma zero" para cada um dos demais efeitos);

b_j: é o efeito do bloco j (j = 1,2,...,b), assumido como fixo;

C_k: é o efeito fixo do cruzamento k, incluindo-se testemunha (k = 1,2,...,c, c+1,c+2,...,c+t; sendo c o número de cruzamentos originando progênies e t o número de testemunhas);

g_i(k): é o efeito do genótipo (progênie ou testemunha) i, oriundo do cruzamento k (i = 1,2,...,p_k; p_k é o número de genótipos no cruzamento k), assumido fixo e nulo se i for uma testemunha, ou aleatório com distribuição N(0,) independente, se i for uma progênie relacionada ao cruzamento k; e

e_ijk: é o erro experimental aleatório associado à ijk-ésima parcela, assumido independente e identicamente distribuído, sob N(0,).

Trata-se, portanto, de um modelo misto em que as n observações y_ijk, expressas pelo vetor y_(nx1), podem ser descritas matricialmente pelo modelo linear misto geral (Henderson, 1984):

com:

Neste modelo todos os efeitos fixos estão reunidos no vetor paramétrico b_(px1) e os efeitos aleatórios, no vetor paramétrico g_(qx1), exceto os erros que compõem o vetor e_(nx1); e, X_(nxp) e Z_(nxq) representam as matrizes de incidências dos efeitos contidos em b e g, respectivamente. O objetivo central do trabalho é estimar os componentes de variância nas matrizes R_(n) e G_(q), assumidas: R = I_(n) (onde é matriz identidade) e G =  G_k, com G_k = I_(pk) (indica a operação soma direta das c matrizes G_k, isto é, G é bloco diagonal com ).

Os parâmetros e os casos simulados

Os valores paramétricos foram definidos de maneira a preservar certas características dos ensaios em blocos aumentados de programas de seleção recorrente em espécies autógamas. Procurou-se simular experimentos com coeficientes de variação (CV) médios, com pequeno efeito de blocos e razoável similaridade entre os cruzamentos. Assim, tomou-se: m  = 5 e  = 1, resultando num CV igual a 20% e prevenindo-se contra observações negativas (sob distribuição normal). Quanto ao número de cruzamentos, foram consideradas duas situações: c = 1 e c = 5. Os efeitos de blocos e de cruzamento(s), embora fixos, tiveram seus perfis gerados pela função `normal' do SAS, com as respectivas variâncias:  = 0,20 e  = 0,25. Os efeitos de testemunhas (em número de duas: t = 2) foram fixados em: C_(c+1) = +1 e C_(c+2) = -1. As variâncias genotípicas dentro de cruzamento () também foram escolhidas procurando-se cobrir amplitude já observada para a relação f_g = /, a saber, entre 0 e 4 , em que é a herdabilidade de observações individuais). Nos casos com progênies de uma única origem (c=1), foram considerados seis valores alternativos de (ou simplesmente ): 0,05; 0,25; 0,50; 1,00; 2,00; ou 4,00. E, nos casos com progênies de diferentes origens (c = 5), os valores de foram tomados para duas situações alternativas: i) ensaios com cruzamentos de variâncias genotípicas mais heterogêneas ( = 0,05;  = 0,50;  = 1,00;  = 2,00; e  = 4,00); ou, ii) ensaios com cruzamentos de variâncias genotípicas menos heterogêneas ( = 0,30;  = 0,50;  = 0,70;  = 0,90; e  = 1,10).

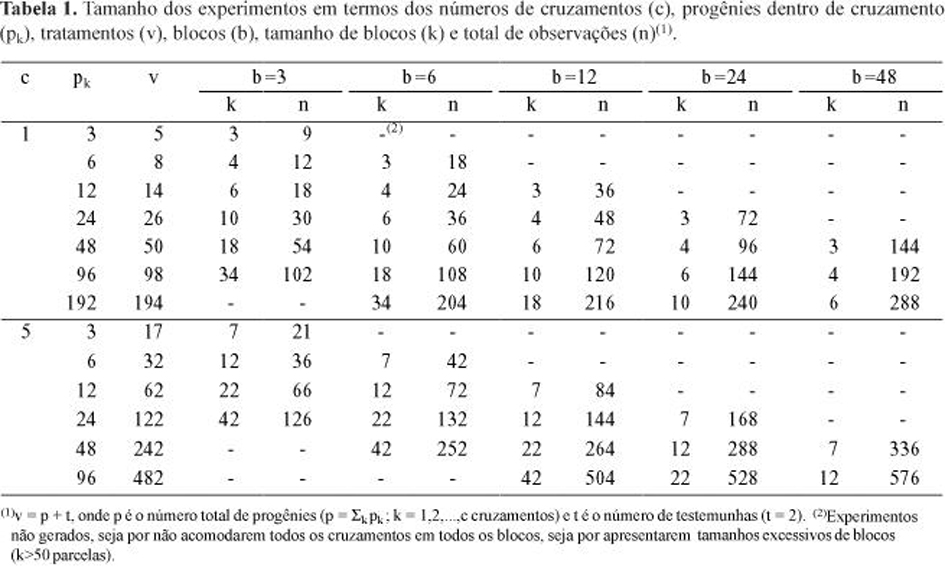
Os tamanhos dos experimentos variaram conforme o número de cruzamentos, o de progênies dentro de cruzamentos e o de blocos, como descrito na Tabela 1. Os cruzamentos foram tomados sempre de maneira ortogonal aos blocos, e o número p_k foi comum para todos os cruzamentos dentro de cada experimento. As combinações de variâncias e tamanhos c, p_k e b perfizeram 178 casos experimentais. Para cada um, foram simulados 50 experimentos, os quais foram submetidos, individualmente, aos diferentes métodos de estimação.

Procedimentos estatístico-computacionais de estimação

A estimação dos componentes (k = 1,2,...,c; com c = 1 ou c = 5) e foi feita por meio de quatro métodos: ANOVA, MIVQUE(0), ML e REML (Rao & Kleffe, 1988; Searle et al., 1992). No método ANOVA, as esperanças de quadrados médios foram obtidas da Soma de Quadrados tipo III do SAS, o que as enquadram na categoria do método 3 de Henderson (Littell & McCutchan, 1987).

Para análise, foram empregados os procedimentos GLM (procedure for general linear models) e MIXED (procedure for mixed linear models) do SAS. Os comandos e instruções para a sua execução são listados a seguir:

Estimação ANOVA (Henderson-3):
proc glm data=ARQ_ORIG;
class BLOCO CRUZ GENOT;
model Y=BLOCO CRUZ GENOT(CRUZ);
contrast `GenCrz1' GENOT(CRUZ) 1 -1 0,
GENOT(CRUZ) 0 1 ¾1;
random GENOT(CRUZ);
lsmeans GENOT(CRUZ)/slice=CRUZ;
run;

O PROC GLM não produz explicitamente as estimativas dos componentes de variância. Mas, lista através do comando `random' a E(QM) para cada fonte de variação no modelo, incluindo a de contrastes especificados (ex: contrast `GenCrz1' ¾ genótipos dentro do Cruzamento 1, assumido com 3 progênies). Assim, as estimativas ANOVA dos componentes de interesse são obtidas igualando-se as expressões de E(QM) aos respectivos quadrados médios:

O coeficiente `K' (função de atributos de tamanho do experimento (Duarte, 2000)) é fornecido numericamente pelo SAS como resultado da utilização do comando `random' do procedimento GLM.

Estimações MIVQUE(0), ML e REML:
proc mixed data=ARQ_ORIG method= ;
class BLOCO CRUZ GENOT;
model Y=BLOCO CRUZ;
random GENOT(CRUZ)/group=CRUZ;
run;

No PROC MIXED a opção `method=' permite escolher entre as outras três alternativas de estimação: `REML', `ML' ou `MIVQUE0'. Basta informar uma destas siglas logo após o sinal `='. Se nada for informado, o procedimento utiliza REML como padrão. Aqui, o comando `random' através da opção `group=' especifica um modelo misto em que os efeitos aleatórios apresentam uma matriz diagonal de componentes de variância, com heterogeneidade entre os cruzamentos e variância comum dentro do k-ésimo cruzamento. Contrariamente ao GLM, o PROC MIXED calcula e fornece diretamente as estimativas dos componentes de variância dos efeitos listados no comando `random'.

Avaliação da qualidade dos estimadores

Considerando-se que, em estudos de simulação, os parâmetros populacionais ( e ; com k = 1,2,...,c) são conhecidos, a avaliação da qualidade de cada estimador é direta. Dois critérios foram utilizados para este propósito: a tendenciosidade (viés) e o erro quadrático médio (eqm). O primeiro, viés = E() - q, avalia a posição das estimativas ( ou ) produzidas por um método, em relação ao respectivo parâmetro q (ou ). Já o segundo, eqm = E( - q)², avalia a dispersão das estimativas em torno de q, para cada parâmetro e método. Valores de baixa magnitude para ambos os critérios indicam boa qualidade do estimador associado.

Resultados e Discussão

Tratamentos novos de uma só população

A presente discussão tem por base a síntese parcial dos resultados, representada pelas Figuras 1 e 2, para as quais foram escolhidas duas relações representativas: f_g = 0,25 e f_g = 2,00 ( = 0,2 e  @ 0,7, respectivamente). Os resultados completos da série de simulações são apresentados por Duarte (2000). Para simplificar a notação, como, neste caso, tem-se k = c = 1 cruzamento, o parâmetro será referido simplesmente como (com estimativas ).

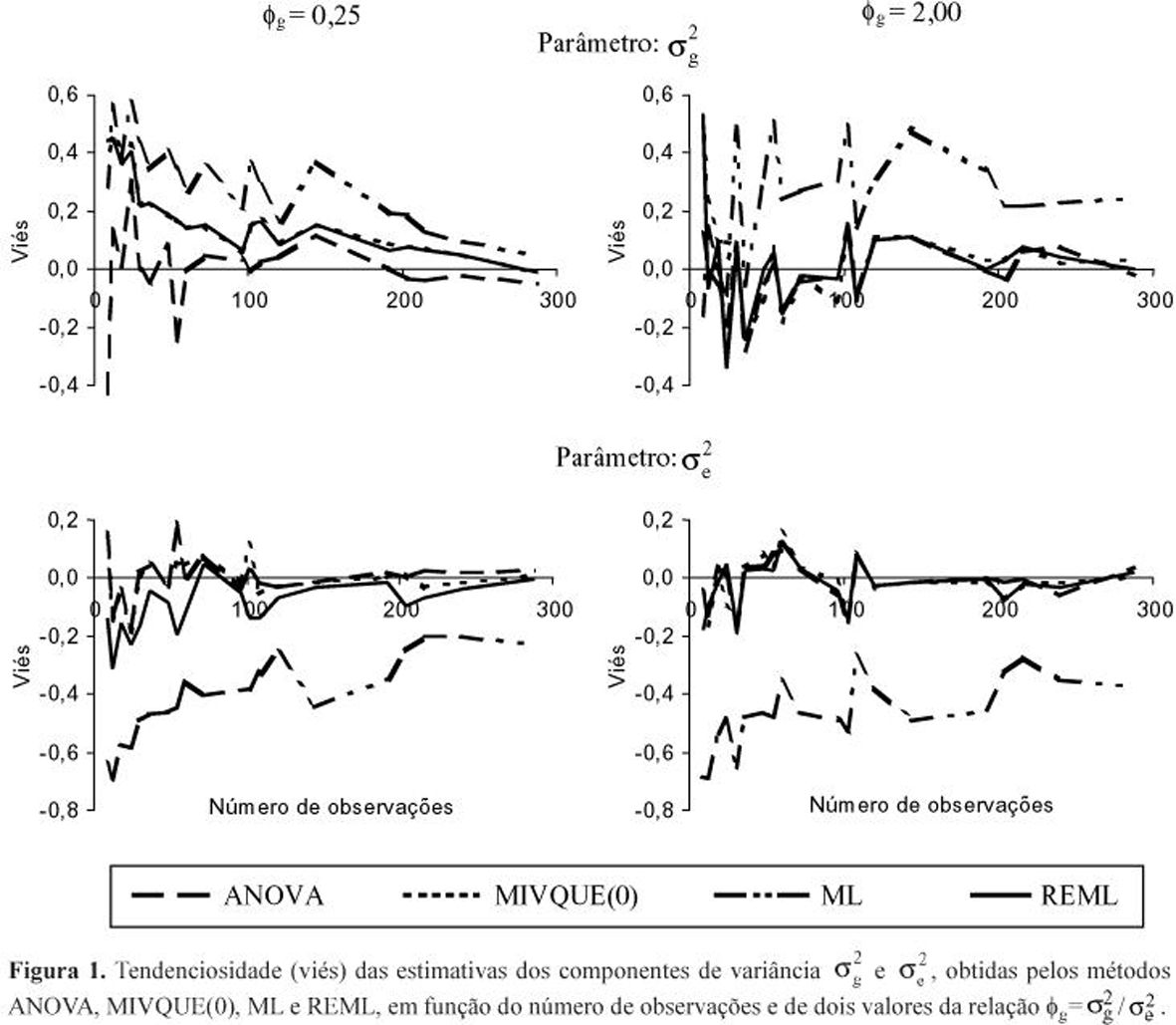
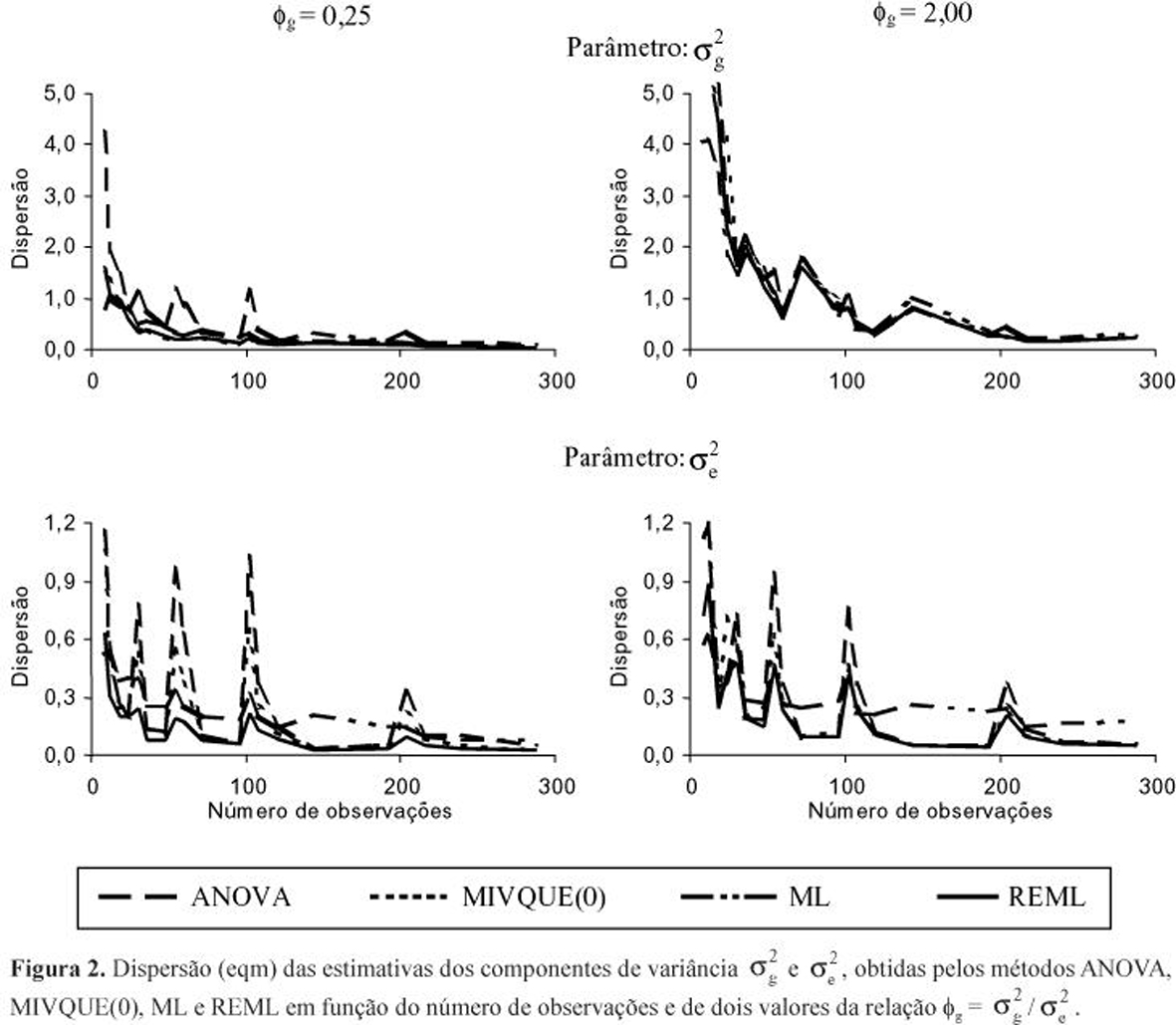
Observando-se o comportamento dos estimadores ANOVA, MIVQUE(0), ML e REML, sob variações no tamanho dos experimentos (n, b e p_k), pôde-se constatar que, para os ensaios maiores (n>200 e b³12), todos os métodos, exceto ML, apresentaram estimativas de boa qualidade. Note-se os vieses (Figura 1) e eqm's (Figura 2) tendendo para zero, em função do aumento no número de observações (n), principalmente para ANOVA, MIVQUE(0) e REML. Apesar desse comportamento similar, as vantagens de um ou outro método puderam ser notadas nos experimentos menores.

É conveniente ressaltar que um número elevado de observações por si só não é suficiente para caracterizar um experimento em blocos aumentados como grande. Notem-se os picos de viés e eqm (Figuras 1 e 2), especialmente para , os quais foram resultantes de casos com pequeno número de blocos, apesar de n crescente por compensação em p_k. Duarte (2000) ilustra o desaparecimento desses picos quando foram tomados apenas os casos com todos os atributos de tamanho (n, b e p_k) crescentes. Assim, se a pesquisa tiver como um de seus objetivos estimar parâmetros do tipo e , mesmo que o número de progênies seja elevado, recomenda-se planejar experimentos com pelo menos dez blocos.

Avaliando-se cada estimador, constata-se que ML mostrou-se tendencioso, tanto para como para , em toda a série dos tamanhos experimentais avaliados (n = 9 a 288, b = 3 a 48, e blocos de tamanho k = 3 a 34). O método produziu consistentemente subestimativas de e superestimativas de (Figura 1). Além disso, os conjuntos de estimativas _ML tenderam a mostrar eqm's quase sempre entre os mais elevados. Diante disso, conclui-se que os estimadores ML não se mostraram apropriados para o modelo em estudo.

Teoricamente, o vício das estimativas ML é atribuído a dois aspectos: i) o fato de o método não levar em conta a perda de graus de liberdade associados à estimação dos efeitos fixos; e ii) em decorrência da imposição de restrição de não-negatividade nos algoritmos de cálculo (Resende et al., 1996). Assim, para se eliminar esse vício é necessário aumentar o número de observações e o de níveis do fator aleatório cujo componente é alvo da estimação. No presente caso, embora a magnitude dos vieses se tenha reduzido com o aumento do tamanho dos experimentos, o método continuou viesado para ambos os parâmetros, até o maior destes tamanhos (p_k = 192, b = 48 e n = 288).

Estes resultados contrariam os de Gonçalves (1984), em que o método ML foi o de melhor desempenho, inclusive em experimentos relativamente pequenos (107 observações) e sob /<1. Deve-se ressaltar que nesse trabalho os efeitos de blocos, além dos de tratamentos adicionais, foram assumidos como aleatórios; e, como se sabe, ML tende a melhorar o seu desempenho quando se reduz o número de efeitos fixos no modelo. Segundo Resende et al. (1996), o vício associado às estimativas ML são tanto maiores quanto maior o posto da matriz X, em relação ao número total de observações. Por esta razão, quando esse posto diminui, ML e REML tendem a produzir resultados similares.

O método REML, nos experimentos menores (n<120 e b£6) e com relação f_g<1, embora em menor intensidade, mostrou comportamento similar ao ML em termos de viés. Isto é, um vício para menos nas estimativas de e um vício para mais nas de . Mas, em REML a magnitude dos vieses reduziu-se sensivelmente à medida que se aumentou o tamanho dos experimentos e a relação f_g tornou-se igual ou maior que a unidade (Figura 1). Por outro lado, os resultados sugerem que, embora REML tenha sido proposto para eliminar o vício de ML decorrente dos graus de liberdade dos efeitos fixos (levados em conta em REML, mas não em ML), a fonte de vício relacionada à restrição de não-negatividade continua determinando uma certa tendência. Por isso, quando a relação f_g (ou ) aproximou-se de zero, o método tornou-se nitidamente viesado, sobretudo em experimentos pequenos.

Nos experimentos de maior tamanho (n³240 e b³24), o viés positivo associado às estimativas _REML só permaneceu nos casos com relações f_g<0,25, o que corresponde a <0,2. Já as estimativas de não mostraram mais qualquer tendência perceptível. Logo, REML mostra-se bastante favorável nestas condições. Em termos práticos, se a variabilidade genotípica esperada não for muito baixa (>0,3), o método fornece estimativas razoáveis desde que n³120 e b>6. Ademais, REML apresentou a menor dispersão amostral (eqm) associada às estimativas de e, para , eqm's entre os mais baixos, revezando-se com MIVQUE(0) e ML (Figura 2).

O método ANOVA (Henderson-3) mostrou-se não-tendencioso na estimação dos dois componentes ( e ), sob todas as condições avaliadas (Figura 1). Apesar disso, apresentou grande flutuação nos valores médios de (E()'s), em experimentos menores, e, quase sempre, os maiores valores de eqm, nos conjuntos de estimativas de ambos os parâmetros (Figura 2). Isto logicamente compromete a qualidade de suas estimativas. Ademais, os valores de eqm foram especialmente superiores aos dos métodos concorrentes, para o parâmetro , indicando que numa análise isolada a confiança associada às estimativas ANOVA da variância genotípica é quase sempre a mais baixa. Tais constatações deixam o método em desvantagem em relação a REML e MIVQUE(0), sobretudo no caso de experimentos pequenos (n£120; b£6 e p_k£48).

Estes resultados confirmam a indicação da literatura de que os estimadores ANOVA de componentes de variância não são adequados para modelos mistos com dados desbalanceados (Swallow & Monahan, 1984; Littell & McCutchan, 1987; Rao & Kleffe, 1988; Searle et al., 1992; Kelly & Mathew, 1994). Tal recomendação, contudo, não deve ser generalizada, haja vista as suas estimativas de boa qualidade aqui obtidas nos casos de experimentos relativamente grandes (n>200; b³12 e p_k>48). Situações estas em que o método pode ser utilizado, sem receio, na análise do presente modelo.

Por último, os componentes de variância estimados pelo método MIVQUE(0) mostraram duas características marcantes: i) suas estimativas de aproximaram-se muito das correspondentes estimativas ANOVA; e ii) suas estimativas de sempre se aproximaram daquelas obtidas pelo método REML (Figura 1). Apesar destas semelhanças, o método MIVQUE(0) mostrou superioridade em relação a ambos os concorrentes, em cada uma das situações.

Os conjuntos de estimativas _MIVQUE(0), embora similares aos de _ANOVA, quase sempre exibiram eqm's inferiores (Figura 2). Logo, tais estimativas MIVQUE(0), além de livres de vício, são relativamente de menor variância, isto é, de maior precisão. Os eqm's associados às estimativas _MIVQUE(0) somente superaram os de _REML. Porém, como já discutido, as estimativas REML mostraram-se viesadas negativamente nos experimentos menores. Constata-se, portanto, que MIVQUE(0) possui vantagens sobre os demais métodos para estimar o parâmetro .

Na estimação de , o método MIVQUE(0) comportou-se de forma muito similar a REML, tanto nos valores obtidos (linhas praticamente se confundindo na Figura 1), quanto na dispersão amostral de suas estimativas. Ambos tenderam a mostrar vício positivo para , nos experimentos pequenos (n<120 e b£6) e com baixa variância genotípica relativa (f_g<1 Û <0,5). Mas, na análise de experimentos maiores (n³120 e b>6), o viés praticamente desapareceu, restringindo-se às situações de herdabilidade baixa (<0,3). Assim, os dois métodos destacam-se na estimação do componente , desde que este parâmetro não seja pequeno.

Resultados similares são reportados na literatura. Swallow & Monahan (1984) afirmam que os estimadores de por MIVQUE e ANOVA usualmente diferem pouco. Já a semelhança entre as estimativas MIVQUE e REML de talvez se justifique pela normalidade dos dados, uma vez que diante disso a versão MIVQUE iterativa (I-MIVQUE) equivale a REML (Swallow & Monahan, 1984; Sorensen & Kennedy, 1986). Ademais, no PROC MIXED do SAS, a estimação de componentes de variância por REML é feita iterativamente, tomando-se as estimativas MIVQUE(0) como valores de partida. Neste sentido, os resultados sugerem que as iterações não conseguiram melhorar a qualidade das estimativas iniciais, apesar de um maior consumo de tempo e de recursos computacionais em relação ao método não iterativo (MIVQUE-0).

O gasto em memória computacional e tempo em CPU, de fato, pode ser substancial na análise de experimentos grandes e com elevado número de níveis do fator aleatório (progênies). Sorensen & Kennedy (1986) alertam para o problema ao referirem-se aos dois métodos: "a menos que a qualidade das estimativas REML seja bastante superior, a preferência do analista recairá sobre os estimadores MIVQUE". Seraphin (1984) também indicou este método para um modelo estatístico de tratamentos hierárquicos, semelhante ao aqui avaliado, sobretudo por sua rapidez e eficiência. Littell et al. (1996) acrescentam que MIVQUE pode ainda ser útil quando os processos iterativos falham em atingir convergência. Logo, a vantagem de se optar pelo método MIVQUE(0) em detrimento de REML pode ser consideravelmente grande.

Nos experimentos pequenos, o ganho relativo ao se fazer esta opção resulta do fato de que REML produziu estimativas viesadas para , enquanto MIVQUE(0) o fez imparcialmente. Um bom desempenho de MIVQUE(0) em comparação a REML, em experimentos relativamente pequenos (situação em que a maioria dos métodos falham) e com relação /³1, também foi constatado por Gonçalves (1984), num modelo de blocos aumentados.

Uma insatisfação geral com relação aos estimadores MIVQUE é o fato de exigirem, no seu cálculo, valores a priori para os componentes de variância (ou para razões do tipo f_g). Assim, sob desbalanceamento, esses estimadores são ditos de variância mínima apenas localmente, isto é, somente quando os valores preestabelecidos forem corretos (Swallow & Monahan, 1984). Todavia, Sorensen & Kennedy (1986) asseguram que, numa população sem seleção, as estimativas MIVQUE permanecem não viesadas, mesmo sob valores a priori incorretos, embora não sejam mais de variância mínima. Outros estudos indicam que, mesmo sob atribuições paramétricas equivocadas, MIVQUE ainda produz estimativas com menor variância do que ANOVA, sobretudo para os outros componentes que não o erro (Swallow & Searle, 1978; Rao & Kleffe, 1988). Portanto, as vantagens aqui evidenciadas em relação aos métodos ANOVA e REML parecem não depender dos valores iniciais ( = 1 e  = 0).

Finalmente, pôde-se constatar que um problema de ordem prática ainda permanece: nenhum método se mostrou adequado para estimar quando a relação f_g foi muito baixa e os atributos de tamanho experimental foram pequenos (n<120, b<6 e p_k<24). Assim, cabe aos melhoristas planejar os seus ensaios com atenção especial a tais atributos, procurando garantir tamanhos razoáveis de n, b e p_k, sobretudo quando a diferenciação esperada entre os materiais genéticos for pequena.

Tratamentos novos de diferentes populações

No caso de progênies de diferentes cruzamentos, a discussão será ilustrada pelas Figuras 3 e 4. Aqui, como estes tratamentos tiveram origens distintas (c = 5 cruzamentos), retorna-se à notação original (k = 1,2,...,c) para a variância de genótipos dentro de cruzamentos.

A princípio, vale reportar que os métodos não sofreram influências diferenciadas importantes, em viés e eqm, advindas do fato de os cruzamentos apresentarem, entre si, variâncias genotípicas mais ou menos heterogêneas. Isto é notório sobretudo na estimação do parâmetro (parte superior da Figura 3). No caso de , apesar da similaridade dos comportamentos relativos, houve tendência de os métodos melhorarem mais rapidamente a qualidade de suas estimativas e produzirem resultados mais parecidos entre si, sob menor heterogeneidade das variâncias .

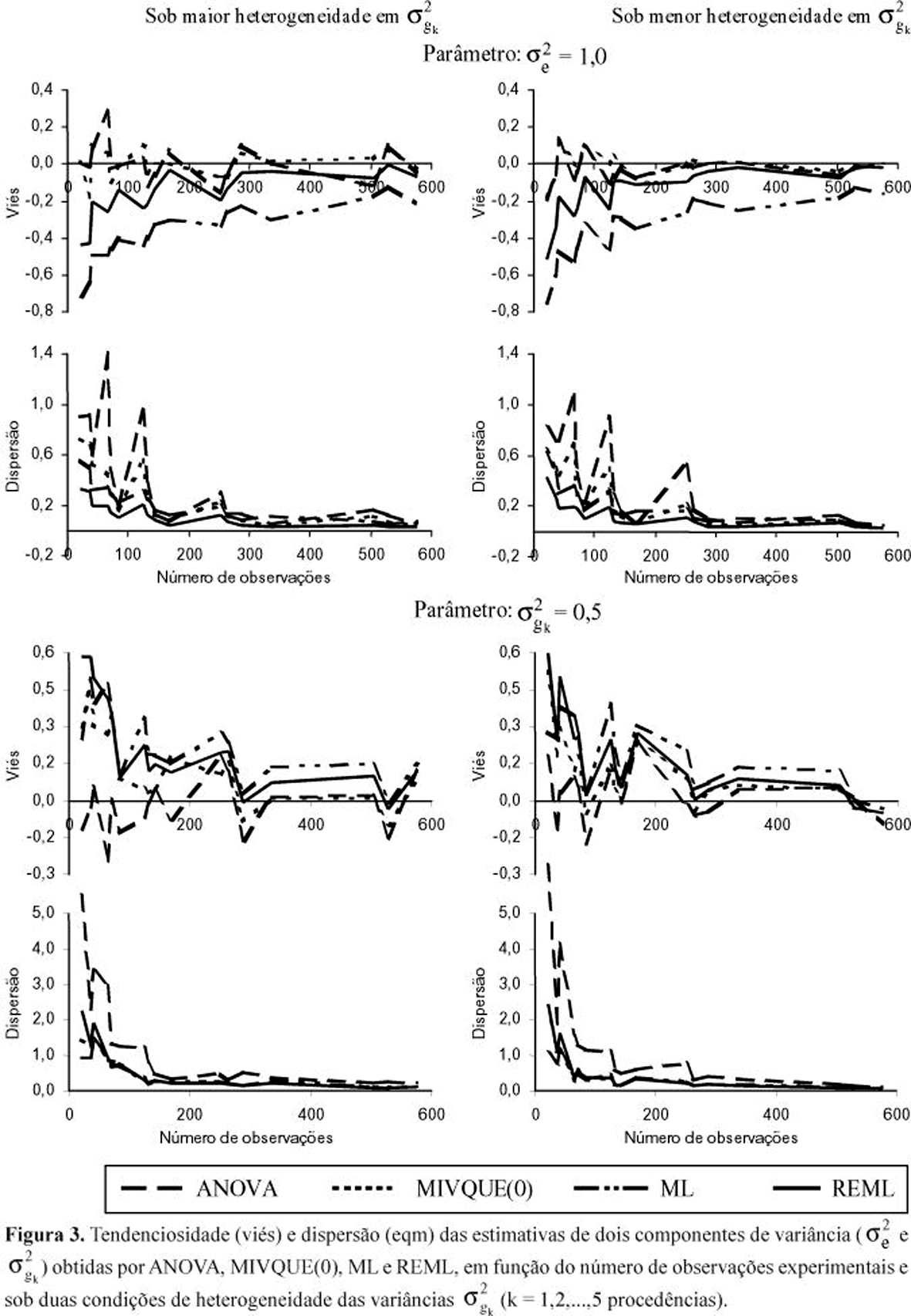
De outro modo, os atributos de tamanho experimental (n, b e p_k) exerceram influência diferenciada marcante sobre os métodos de estimação. Observe-se novamente os picos de eqm, sob n crescente, nítidos para as estimativas _ANOVA e _MIVQUE(0), os quais resultam de casos com pequeno número de blocos (b = 3). Os resultados indicam que a precisão destas estimativas, sobretudo _ANOVA, é muito afetada pela redução do número de blocos. Já as estimativas _REML e _ML são menos influenciadas por este aspecto, apesar de evidenciarem nítida tendenciosidade sob n baixo, contrariamente a _ANOVA e _MIVQUE(0) (Figura 3).

Na estimação de , outro fator que exerceu forte impacto sobre a qualidade das estimativas foi a relação  = /. Tal como nos casos de c = 1, também aqui (c = 5), quanto menor o valor de (ou da herdabilidade básica ) maior é a chance de os métodos produzirem estimativas diferenciadas, sobretudo quando se reduz o tamanho do experimento (Figura 4). Note-se a tendência de maior aproximação das linhas de diferentes métodos, tanto para viés como para eqm, da esquerda para a direita em cada gráfico e de cima para baixo na Figura como um todo.

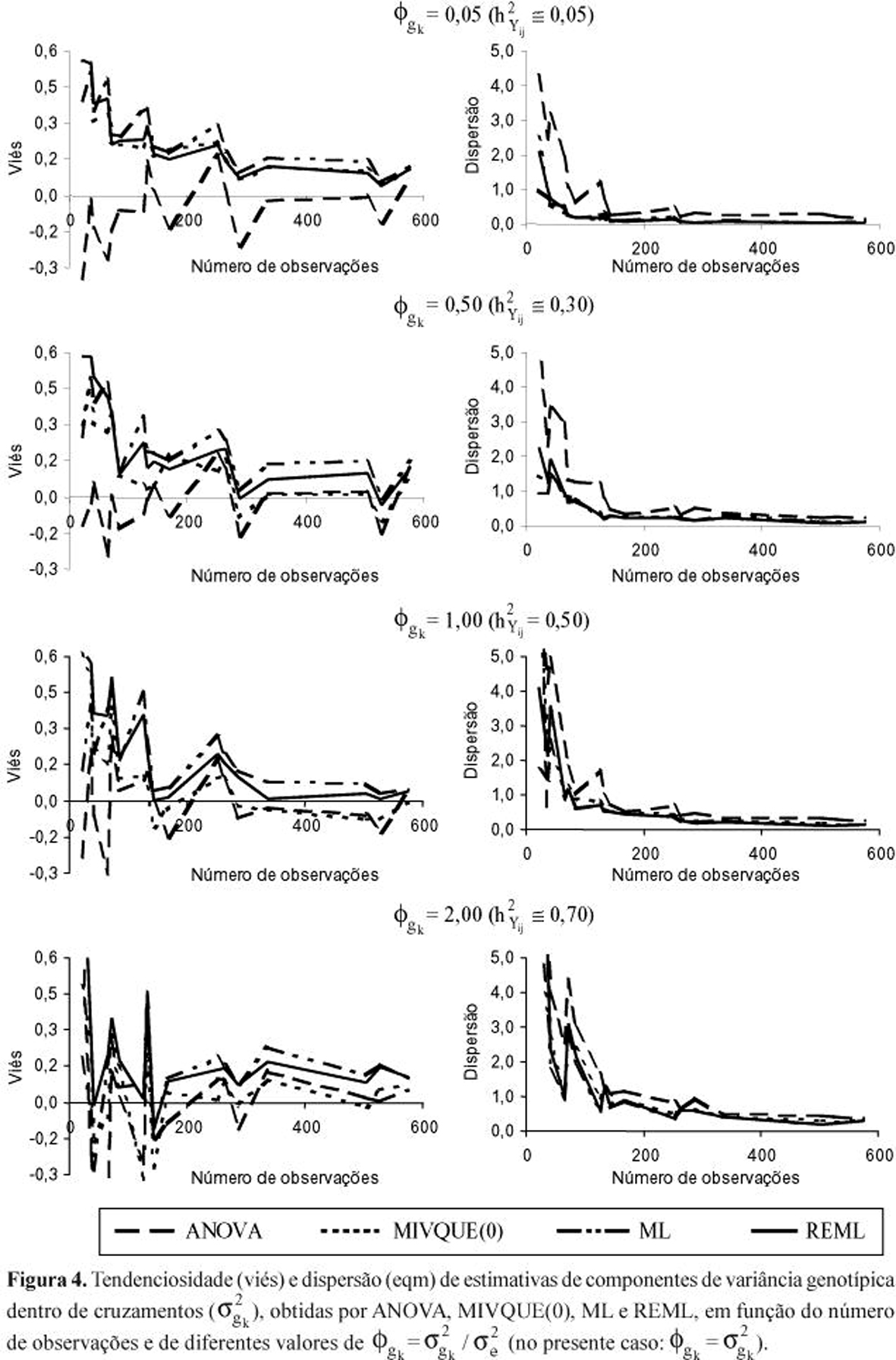
Exceto ANOVA, que não evidenciou vício para quaisquer dos parâmetros, embora sempre com os maiores valores de eqm, os outros três métodos produziram superestimativas de quando a relação foi baixa. Isto, particularmente quando os experimentos foram pequenos (n£120; b<12; p_k<12) e os valores paramétricos (k = 1,2,...,5) diferenciaram-se mais entre os cruzamentos. Tal constatação indica que, em populações com baixa variabilidade genética, estes métodos tendem a superestimar as suas variâncias e, conseqüentemente, o ganho esperado com a seleção intrapopulacional; a menos que os atributos de tamanho amostral ultrapassem aqueles limites mínimos, pois em experimentos um pouco maiores (n = 240; b = 12; p_k = 12) a superestimação só se manteve sob £0,5 (ou £0,3).

Em síntese, o comportamento relativo dos métodos mostrou-se similar à situação em que as progênies originaram-se de um único cruzamento. Assim, inspecionando-se as Figuras 3 e 4 constata-se: i) o método ANOVA destacou-se por ser livre de tendência, tanto na estimação de como na de , porém, mostrou sempre estimativas com a maior dispersão amostral (limitação superada em experimentos grandes); ii) o método MIVQUE(0) produziu estimativas de melhor qualidade do que ANOVA, pois, além de serem livres de vício, possuem uma menor dispersão (eqm), sobretudo nos experimentos menores; iii) as estimativas _MIVQUE(0), apesar de viesadas positivamente em experimentos de pequeno tamanho (n<72; b£6; p_k<12) e sob £0,5, mostraram eqm inferiores às _ANOVA; iv) o método ML produziu subestimativas de e superestimativas de , sob £1, com vícios crescentes quando se reduz o tamanho dos experimentos (abaixo de n = 168, b = 12 e p_k = 24); v) as estimativas _REML, embora as mais uniformes (menores eqm's), foram também tendenciosas negativamente até tamanhos experimentais de n = 120 e b = 12; e, vi) as estimativas REML de estiveram sempre entre as de pior qualidade, tanto em viés (positivo) quanto em eqm, sobretudo nos experimentos de menor tamanho.

A novidade em relação aos casos de c = 1 foi, portanto, o pior desempenho relativo do método REML, na estimação dos parâmetros (k = 1,2,...,c), inclusive em comparação a ML. Assim, quando as progênies vieram de diferentes cruzamentos, os métodos de máxima verossimilhança também não mostraram vantagens comparativas que justifiquem os maiores recursos computacionais envolvidos. Suas propriedades ideais só foram garantidas nos experimentos de maior tamanho. Mas, nestas condições, os métodos MIVQUE(0) e ANOVA produzem estimativas de igual qualidade.

O método MIVQUE(0) mais uma vez destacou-se por fornecer estimativas livres de vício como o ANOVA e, adicionalmente, com variância relativamente baixa. Quanto ao vício positivo associado às suas estimativas , sob relações muito baixas e experimentos de pequeno tamanho, praticamente desapareceu quando >0,5 e os experimentos atingiram tamanhos usuais na prática.

Por fim, acrescenta-se que no caso de c = 5 ainda persiste o problema de estimar para os cruzamentos de variabilidade genética reduzida, cujas progênies forem testadas em experimentos pequenos. Pôde-se observar também que nenhum método produziu estimativas de qualidade para quando o número de progênies por cruzamento foi muito baixo (p_k<12). Assim, recomenda-se mais uma vez atenção especial aos atributos n, b e p_k, no planejamento experimental, sobretudo quando se esperam populações com variabilidades intrínsecas baixas.

Conclusões

1. Em experimentos grandes (n>200 observações, b³12 blocos e p_k³24 progênies por cruzamento) todos os métodos, exceto ML, garantem boa qualidade às estimativas dos componentes de variância.

2. O método ML preserva algum vício (positivo para as estimativas de e negativo para as de ) mesmo sob n = 288 e b = 48 (cada bloco com seis parcelas).

3. À medida que se reduz o tamanho dos experimentos, os métodos ML, REML e MIVQUE(0) tendem a superestimar a(s) variância(s) genotípica(s) , sobretudo quando a razão / decresce; ML é o método mais viesado e de maior variância, quando os novos genótipos têm origem única; e MIVQUE(0) é o de melhor desempenho quando os genótipos têm procedências diferentes.

4. O método ANOVA, embora não tendencioso, apresenta estimativas de baixa precisão.

5. Na estimação de , o método MIVQUE(0), à semelhança de ANOVA, não exibe tendenciosidade, enquanto REML tende a subestimá-la cada vez mais à medida que se reduzem o tamanho do experimento e a relação /; em comparação ao método ANOVA, MIVQUE(0) tem a vantagem de produzir estimativas de de melhor precisão.

Agradecimentos

Ao Centro de Informática na Agricultura do Campus "Luiz de Queiroz" da Universidade de São Paulo (Ciagri/USP), pela disponibilização de recursos computacionais.

 

Referências

• DUARTE, J. B. Sobre o emprego e a análise estatística do delineamento em blocos aumentados no melhoramento genético vegetal. Piracicaba : Esalq, 2000. 293 p. Tese de Doutorado.
• FEDERER, W. T. Augmented (or hoonuiaku) designs. Hawaiian Planters' Records, Aiea, v. 55, p. 191-208, 1956.
• FISHER, R. The correlation between relatives on the supposition of Mendelian inheritance. Royal Society of Edinburgh Transactions, Edinburgh, v. 52, p. 399-433, 1918.
• GONÇALVES, N. M. Comparação de diversas metodologias para a análise de um delineamento aumentado com tratamentos fixos e aleatórios. Brasília : UnB, 1984. 99 p. Dissertação de Mestrado.
• HARTLEY, H. O.; RAO, C. R. Maximum-likelihood estimation for the mixed analysis of variance model. Biometrika, Oxford, v. 54, p. 93-108, 1967.
          [ Medline ]
• HENDERSON, C. R. Applications of linear models in animal breeding. Guelph : University of Guelph, 1984. 462 p.
• HENDERSON, C. R. Estimation of variance and covariance components. Biometrics, Washington, v. 9, p. 226-252, 1953.
• KELLY, R. J.; MATHEW, T. Improved nonnegative estimation of variance components in some mixed models with unbalanced data. Technometrics, Alexandria, v. 36, p. 171-181, 1994.
• LITTELL, R. C.; McCUTCHAN, B. G. Variance component estimation with the SAS system. In: ANNUAL CONFERENCE OF SAS USER GROUP INTERNATIONAL, 12., 1987, Dallas. Proceedings... Dallas : SAS Users Group International, 1987. p. 1168-1173.
• LITTELL, R. C.; MILLIKEN, G. A.; STROUP, W. W.; WOLFINGER, R. D. SAS system for mixed models. Cary : SAS Institute, 1996. 633 p.
• PATTERSON, H. D.; THOMPSON, R. Recovery of inter-block information when block sizes are unequal. Biometrika, Oxford, v. 58, p. 545-554, 1971.
• RAO, C. R. Estimation of variance and covariance components: MINQUE theory. Journal of Multivariate Analysis, San Diego, v. 1, p. 257-275, 1971a.
• RAO, C. R. Minimum variance quadratic unbiased estimation of variance components. Journal of Multivariate Analysis, San Diego, v. 1, p. 445-456, 1971b.
• RAO, C. R.; KLEFFE, J. Estimation of variance components and applications. New York : Elsevier Science, 1988. 370 p.
• RESENDE, M. D. V. de; PRATES, D. F.; YAMADA, C. K.; JESUS, A. de. Estimação de componentes de variância e predição de valores genéticos pelo método da máxima verossimilhança restrita (REML) e melhor predição linear não-viciada (BLUP) em Pinus. Boletim de Pesquisas Florestais, Colombo, n. 32/33, p. 23-42, jan./dez. 1996.
• SEARLE, S. R.; CASELLA, G.; McCULLOCH, C. E. Variance components. New York : J. Wiley, 1992. 501 p.
• SERAPHIN, J. C. Comparação numérica de três estimadores de componentes de variância em alguns modelos genético-estatísticos de cruzamentos. Piracicaba : Esalq, 1984. 74 p. Dissertação de Mestrado.
• SORENSEN, D. A.; KENNEDY, B. W. Analysis of selection experiments using mixed model methodology. Journal of Animal Science, Champaign, v. 63, p. 245-258, 1986.
          [ Medline ]
• SWALLOW, W. H.; MONAHAN, J. F. Monte Carlo comparison of ANOVA, MIVQUE, REML, and ML estimators of variance components. Technometrics, Alexandria, v. 26, p. 47-57, 1984.

João Batista Duarte(2), Roland Vencovsky(3) e Carlos Tadeu dos Santos Dias(4)
ctsdias[arroba]carpa.ciagri.usp.br

1) Aceito para publicação em 27 de julho de 2000.
Extraído da Tese de Doutorado, apresentada pelo primeiro autor à Escola Superior de Agricultura "Luiz de Queiroz" (Esalq), Piracicaba, SP.
(2) Universidade Federal de Goiás, Escola de Agronomia, Caixa Postal 131, CEP 74001-970 Goiânia, GO.
(3) Esalq, Dep. de Genética, Caixa Postal 83, CEP 13418-900 Piracicaba, SP. Bolsista do CNPq.
(4) Esalq, Dep. de Ciências Exatas, Caixa Postal 9, CEP13418-900 Piracicaba, SP.