Valores Propios y Vectores Propios (Eigenvalores y Eigenvectores)

Introducción

En álgebra lineal, los vectores
propios, autovectores o eigenvectores de
un operador lineal son los vectores no nulos que,
cuando son transformados por el operador, dan lugar a un
múltiplo escalar de sí mismos, con lo que no
cambian su dirección. Este escalar ? recibe el
nombre valor propio, autovalor, valor
característico o eigenvalor. A menudo, una
transformación queda completamente determinada por sus
vectores propios y valores propios.

Un espacio
propio, autoespacio o eigenespacio es
el conjunto de vectores propios con un valor propio
común.

La palabra alemana eigen, que se traduce en
español como propio, se usó por primera vez en
este contexto por David Hilbert en 1904 (aunque
Helmholtz la usó previamente con un significado
parecido). Eigen se ha traducido también
como inherente, característico o el
prefijo auto-, donde se aprecia el énfasis en la
importancia de los valores propios para definir la naturaleza
única de una determinada transformación lineal. Las
denominaciones vector y
valor característicos también se utilizan
habitualmente

OBJETIVOS:

• Formular la definición de Valor Propio y de
  Vector Propio (real o complejo).

• Enunciar e interpretar el significado del teorema
  sobre la condición de subespacio vectorial, de un
  subconjunto de vectores propios.

• Enunciar e interpretal el significado del teorema
  relativoa vectores propios pertenecientes a subespacios
  propios diferentes.

• Aplicarlos resultados de las definiciones y teoremas
  estudiados, a la determinación de los valores propios
  y de los subespacios propios.

• Formular la definición de base
  propia.

• Enunciar e interpretar el significado del teorema
  sobre la diagonalización, en el caso de que los
  valores propios sean reales y desiguales y también
  complejos.

• Formular la definición de matrices
  simétricas y diagonalización
  ortogonal.

• Aplicar los conocimientos del capítulo al
  crecimiento de una población y a las Formas
  Cuadráticas.

• Aplicar los resultados del teorema anterior a la
  resolución de ejercicios.

Valores propios y
vectores propios (eigenvalores y eygenvectores) de matrices
reales y complejas

A continuación se va a desarrollar un tema muy
importante dentro del algebra lineal, llamado valor propio y se
plantea de la siguiente manera:

Los términos valor propio y vector propio
correspondientes a los términos eigenvalor y eigenvector
derivados del término alemán Eigenwert cuyo
significado es "valor propio"

Interpretación geométrica en el plano
R2

VALORES PROPIOS Y VECTORES PROPIOS DE UNA
MATRIZ

Definición:

A esta ecuación se la denomina ecuación
característica de A.

• Ejemplo:

Observaciones:

Si A es una matriz de orden nxn entonces las siguientes
afirmaciones son equivalentes:

Solución:

La ecuación característica de
A es:

3.1.- PROCESOS PARA DETERMINACIÓN DE VALORES
PROPIOS Y VECTORES PROPIOS.

Sea A una matriz nxn:

Observación:

Todo endomorfismo en V donde V es un espacio vectorial
de dimensión finita y mayor o igual a 1 sobre el cuerpo de
los complejos admite vectores propios.

Pero si el cuerpo no es complejo, entonces no existen
vectores propios.

• Ejemplo:

El sistema admite solución no trivial
si:

Teorema:

Demostración:

La matriz de f respecto de la base [ V ] se obtiene
determinando las imágenes de los vectores de dicha base, y
teniendo en cuenta la definición de vector
propio

Observación:

POLINOMIO CARACTERISTICO DE UNA MATRIZ

Definición:

PROPIEDADES:

VALORES CARACTERISTICOS PARA MATRICES
TRIANGULARES

Si A es una matriz triangular nxn entonces sus valores
propios son sus elementos en la diagonal principal.

3.2.- MATRICES SEMEJANTES:

Sean las matrices A y B de orden nxn se dice que la
matriz A es semejante a la matriz B si existe una matriz P
invertible de orden nxn tal que B = P-1AP

Observación:

La definición dada también se puede
expresar así:

Las matrices A y B de orden nxn son semejantes si y solo
si existe una matriz invertible P tal que PB = AP

• Ejemplo:

Teorema:

Si A y B son matrices semejantes de orden nxn, entonces
A y B tienen elmismo polinomio característico y por lo
tanto, tienen losmismos valores propios.

Demostración:

Esto significa que A y B tienen la misma
ecuacióncaracterísticay como los valores propios
son raíces de la ecuación característica
tienen los mismos valores propios.

3.3.- EJERCICIOS

2.- Encuentre los autovalores y
autovectores correspondientes a las siguientes transformaciones
lineales:

3.- Obtener los eigenvalores y los
eigenvectores asociados si existen de la siguiente
matriz:

Por lo tanto los eigenvectores de la matriz A son (1,0)
(1,1)

Posibles valores: a= 1; d = 1

5.-Determine los valores
característicos de la siguiente matriz:

Lo cual implica que los valores
característicos de A son -1, 6, -2

6.-Vea si las matrices D y A son
semejantes dada la matriz P

Diagonalización de matrices

Se dice que una matriz cuadrada A es diagonizable, si
existe una matriz inversible P tal que P-1AP sea diagonal; se
dice que la matriz P diagonaliza a la matriz A.

S existe una matriz ortogonal P tal que P-1AP es
diagonal, entonces A es diagonizable, y se dice que P diagonaliza
ortogonalmente a A.

• Ejemplo:

Teorema:

Una matriz A de orden nxn es diagonizable si y solo si
tiene n vectores propios linealmente independientes.

En tal caso la matriz diagonal D semejante a A esta dado
por:

Demostración:

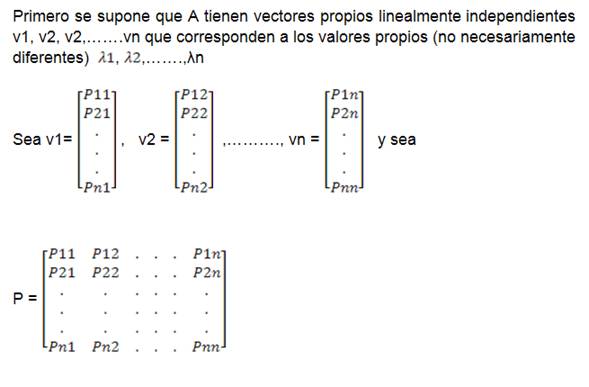
Entonces P es invertible ya que sus columnas son
linealmente independientes.

Ahora también.

Entonces AP = PD y como P es inversible, se puede
multiplicar ambos lados por la izquierda por P-1 para
obtener:

D = P-1AP

Nota:

Si A es una matriz de orden nxn, entonces las siguientes
afirmaciones son equivalentes:

• A es diagonizable.

• A tiene vectores propios linealmente
  independientes.

Nota:

Si una matriz A de orden nxn tiene n valores propios
diferentes entonces A es diagonizable.

• Ejemplo:

Determinar si la siguiente matriz es
diagonizable:

Solución:

Calculando los valores propios de lamatriz A

Poniendo en la forma escalonada en los renglones
reducida:

Para verificar la independencia lineal de los vectores
se forma la matriz P, cuyas columnas son los vectores propios y
se convierte enlaforma escalonada reducida.

4.1.- PASOS PARA DIAGONALIZAR UNA MATRIZ
CUADRADA:

Sea A una matriz nxn:

• 1) Determine n vectores propios linealmente
  independientes v1, v2, v3,…..vn de A, con valores
  propios correspondientes ?1, ?2, ?3,…….?n. Si
  no existen n vectores propios linealmente independientes,
  entonces A no es diagonizable.

• 2) Si A tiene n vectores propios linealmente
  independientes, entonces sea P la matriz nxn cuyas columnas
  son tales vectores propios. Es decir:

P = [v1, v2, v3,………vn]

• 3) La matriz diagonal D = P-1AP tendrá
  los valores propios ?1, ?2, ?3,…….?n en su
  diagonal principal (y ceros en el resto). Observe que el
  orden de los vectores propios usados para formar P determina
  el orden en que aparecen los valores propios sobre la
  diagonal principal de D.

4.2.- EJERCICIOS

Concluimos que A sí es diagonizable.

2.- Encontrar la matriz P que
diagonalice a la matriz A.

Solución:

Buscamos los vectores propios de A. Como es una matriz
de 3×3 entonces debe tener tres vectores propios para ser
diagonizable.

Como A es una matriz triangular superior, sabemos que
los valores propios son los elementos de la diagonal
principal.

Finalmente formamos la matriz P que está
constituida por los vectores propios como vectores
columna.

3.- Demuestre que la matriz dada no es
diagonizable.

Por tanto A no tiene dos vectores característicos
linealmente independientes, entonces se concluye que Ano es
diagonizable.

4.-Demuestre que la matriz dada no es
diagonizable.

Por tanto A no tiene dos vectores característicos
linealmente independientes, entonces se concluye que Ano es
diagonizable.

5.- Calcular A6 donde la matriz A es
igual a:

Aquí aplicamos la ecuación del
cálculo de las potencias de una matriz.

Matrices
simétricas y diagonalización ortogonal

5.1.- MATRIZ SIMETRICA:

Definición:

Una matriz cuadrada es simétrica si:

Observación:

• Una matriz no simétrica puede no ser
  diagonizable.

• Una matriz no simétrica puede tener valores
  propios que no sean reales.

• Para una matriz no simétrica, el numero de
  vectores propios linealmente independientes correspondientes
  a un valor propio puede ser menor que la multiplicidad del
  valor propio.

Ninguno de los casos anteriores es posible con una
matriz simétrica.

Teorema:

Si A es una matriz simétrica nxn, entonces las
siguientes afirmaciones son verdaderas:

Demostración:

La demostración no es posible ya que se requiere
conocimientos más avanzados.

• Ejemplo:

5.2.- MATRIZ ORTOGONAL

Definición:

Teorema:

Una matriz P nxn es ortogonal si y solo si sus vectores
columna forman un conjunto ortonormal.

Demostración:

Suponga que los vectores columna de P forman un conjunto
ortonormal.

Por lo tanto, la matriz compuesta de productos punto es
de la forma

Teorema:

Si A es una matriz simétrica nxn. Si ?1 y ?2 son
valores propios distintos de A entonces sus vectores propios
correspondientes x1 y x2 son ortogonales.

Demostración:

• Ejemplo:

Por consiguiente

X1.x2 = (s, -s). (t, t) = st – st = 0

Y se concluye que x1 y x2 son ortogonales.

5.3.- DIAGONALIZACIÓN
ORTOGONAL:

Una matriz es diagonizable ortogonalmente si existe una
matriz P tal que

P-1AP = D

Teorema:

Si A es una matriz nxn. Entonces A es diagonizable
ortogonalmente y tiene valores propios reales si y solo si A es
simétrica.

Demostración:

Por consiguiente, A es simétrica.

Observación:

El conjunto de matrices diagonizable ortogonalmente es
precisamente el conjunto de matrices
simétricas.

• Ejemplo:

Ahora normalizamos estos vectores:

5.4.- PROCESO DE DIAGONALIZACION ORTOGONAL DE UNA
MATRIZ SIMETRICA:

Sea A una matriz simétrica nxn

• a) Determine todos los valores propios de A y
  la multiplicación de cada uno.

• b) Para cada valor propio de multiplicidad 1,
  elija un vector propio unitario (Elija cualquier vector
  propio y después normalícelo).

• c) Para cada valor propio de multiplicidad
  k2 encuentre un
  conjunto de k vectores propios linealmente independientes. Si
  este conjunto no es ortonormal, aplique el método de
  ortonormalizacion de Gran-Schmidt.

• d) La composición de los pasos b) y c)
  da un conjunto ortonormal de n vectores propios. Use estos
  vectores propios para formar las columnas de P. La matriz
  P-1AP = PTAP = D será diagonal.

5.5.- EJERCICIOS:

1.-Determine si la matriz dada es
ortogonal.

2.- Encuentre una matriz ortogonal P tal
que PTAP diagonalize a A. Compruebe que PTAP da la forma diagonal
correcta.

Ahora hacemos la comprobación:

3.- Encuentre una matriz P que
diagonalize ortogonalmente a A.

Los dos vectores son de multiplicidad 1; por los tanto
los normalizamos para obtener una base ortonormal.

4.- Encuentre los valores propios de la
matriz simétrica dada. Para cada valor propio, determine
la dimensión del espacio propio
correspondiente.

Solución:

Encontramos los valores propios de A.

Por lo tanto tenemos que la dimension del espacio propio
es 2.

5.-Encuentre una matriz
ortogonal P que diagonalice a

Potencias de
matrices. Ecuaciones en diferencias

6.1.-POTENCIAS DE
MATRICES:

Una primera aplicación a la
diagonalización de una matriz es que se puede
fácilmente encontrar la potencia n-ésima de una
matriz.

6.2.- ECUACIONES EN DIFERENCIAS:

Una ecuación en
diferencia es una expresión que relacióna
distintas sucesiones, siendo una de ellas una
sucesión desconocida.

Son similares a las ecuaciones diferenciales,
sustituyendo las funciones por sucesiones.

Las combinaciones lineales de soluciones de
la forma indicada arriba también son
soluciones.

6.3.- EJERCICIOS:

1.- Elevar la matriz dada al cuadrado al
cubo y a la cuarta potencia

2.- Elevar la matriz a la n-esima
potencia

Dado

Solucion:

Aplicando lo ya antes demostrado obtenemos la potencia
hay que tomar en cuenta que si no tenemos la matriz D tenemos que
obtenerla mediante la diagonalización. Además de
obtener P y P inversa.

3.- Encontrar la matriz
potencia de:

Solución:

Para este ejercicio se considera que ya
previamente se a realice do la diagonalización y las
matrices P y D son:

4.-Utilice la
expresión del ejercicio anterior para calcular la potencia
cuando

n=5

Solución:

5.- Dado

Calcular la cuarta potencia

Solución:

Realizando la multiplicación
tenemos

Matrices unitarias,
normales y matrices hermitianas

Los problemas que implican la diagonalización de
matrices complejas, así como los problemas asociados de
valores característicos, requieren del concepto de
matrices unitarias y Hermitianas. Estas matrices corresponden
grosso modo a las matrices reales ortogonales y
simétricas. Para definir las matrices unitarias y
Hermitianas definiremos primero los siguientes
conceptos:

Definición de la Transpuesta Conjugada de una
MatrizTranspuesta:

La transpuesta conjugada de una matriz transpuesta A,
denotada por A*, se define como:

Donde los elementos de A son los conjugados complejos de
los elementos correspondientes de A.

Observación:

Hay que tener presente que si A es una matriz real,
entonces:

7.1.- MATRICES UNITARIAS:

Una matriz compleja A se denomina unitaria
si:

Teorema:

Una matriz compleja A nxn es unitaria si y solo si sus
vectores renglón (o columna) forman un conjunto ortogonal
en Cn

7.2.- MATRICES NORMALES:

Una matriz es normal si conmuta con su
traspuesta, esto es, si AAT = ATA. Obviamente,
si A es simétrica, anti
simétrica u ortogonal, es necesariamente
normal.

7.3.- MATRICES HERMITIANAS:

Se dice que una matriz cuadrada A es hermitiana
si:

A = A*

Así como las matrices simétricas, las
matrices Hermitianas pueden identificarse fácilmente por
inspección. Para probar esto consideremos una matriz de
2×2.

Resultados semejantes pueden obtenerse para matrices
Hermitianas de orden nxn. En otras palabras, una matriz cuadrada
A es hermitiana si y solo si se cumplen las condiciones
siguientes:

• 1. Los elementos de la diagonal principal son
  reales.

• 2. El elemento aij en la i-esima columna es el
  conjugado complejo del elemento aji en el j-ésimo
  renglón y en la i-esima columna.

Teorema: Los valores característicos de
una Matriz Hermitiana:

Si A es una matriz Hermitiana, entonces sus valores
característicos son números reales.

Demostración:

Teorema: Matrices Diagonalizables
Unitariamente

Si A es una matriz hermitiana nxn, entonces:

• 1. A es diagonalizable unitariamente

• 2. A tiene un conjunto de n vectores
  característicos ortonormales.

Teorema: Vectores característicos de una
Matriz Hermitiana

Comparación de las Matrices Hermitianas y las
Matrices Simétricas:

7.4.- EJERCICIOS:

1.- Demuestre que la siguiente matriz es
unitaria.

2.-Demuestre que la siguiente matriz
compleja es unitaria al demostrar que su conjunto de vectores
renglón forma un conjunto ortonormal en C3

Solución:Sean r1, r2 y r3 definidos como
de la siguiente manera:

De manera semejante r1.r3 = 0 y r2.r3 = 0 y se puede
concluir que (r1,r2,r3) es un conjunto ortonormal.

3.- ¿Cuáles de los
siguientes matrices son Hermitianas?

Solución:

• a) Esta matriz no es hermitiana porque contiene
  un elemento imaginario en su diagonal principal.

• b) Esta matiz es simétrica pero no
  hermitiana porque el elemento en el primer renglón y
  segunda columna no es complejo conjugado del elemento en el
  segundo renglón y primera columna.

• c) Esta matriz es hermitiana.

4.- Encuentre los siguientes valores de
la siguiente matriz Hermitiana.

Lo cual implica que los valores característicos
de A son: -1, 6, -2

Para encontrar los vectores característicos de
una matriz compleja se usa un procedimiento semejante al que se
emplea en una matriz real.

5.- Demuestre que los siguientes
vectores característicos de la matriz hermitiana del
ejercicio anterior son mutuamente ortogonales.

6.- Encuentre una matriz unitaria P tal
que P*AP sea una matriz diagonal, donde

Solución:

Enel ejercicio anterior encontramos los vectores
caracteristicos de A. La matriz P se forma al normalizar estos
tres vectores caracteristicos y usar los resultados para crear
los renglones de P.

Aplicaciones:
crecimiento de una población

Las matrices pueden aplicarse para elaborar modelos que
describan el crecimiento de alguna población en clases de
edad de la misma duración.

Si el tiempo que vive un miembro de la población
es L años entonces las clases de edad se representan por
los n siguientes intervalos:

Numero en la clase de primera edad.

Numero en la clase de segunda edad.

Numero en la clase de la n-esima edad.

Durante un periodo de L/n años, la probabilidad
de que un elemento de la clase de la i-esima edad sobreviva para
convertirse en elemento de laclase de la (i + 1) –esima
edad está dada por pi, donde

Al multiplicar esta matriz de transición de
edades por el vector de distribución de edades durante un
periodo especifico seobtiene el vector de distribución de
edades para el siguiente periodo. Es decir:

Axi = xi+1

• Ejemplo:

Una población de conejos criados en un
laboratorio tiene las siguientes
características:

• a) La mitad de conejos sobrevive el primer
  año. De estos, la mitad sobrevive el segundo
  año. La duración máxima de vida es de
  tres años.

• b) Durante el primer año los conejos no
  producen descendencia. El número medio de descendencia
  es 6 durante el segundo año y 8 durante el tercer
  año.

Actualmente la población de laboratorio consta de
24 conejos en la clase de la primera edad 24 en la segunda y 20
en la tercera. ¿Cuántos habrá en cada clase
de edad en un año?

Solución:

El vector actual de distribución de edades
es

Si el patrón de crecimiento continúa
durante otro año, entonces la población de conejos
será:

A partir de los vectores de distribución de
edades x1, x2, x3 se observa que el porcentaje de conejos en las
tres clases de edad cambia cada año.

8.1.- EJERCICIOS:

1.- Use la matriz A de transición
de edades y el vector x de distribución de edades para
encontrar los vectores de distribución de edades x2 y x3.
Luego encuentre una distribución de edades estable para la
matriz dada.

Ahora encontramos una distribución de edades
estables. Para ello encontramos los valores propios.

2.- Use la matriz A de transición
de edades y el vector x1, de distribución de edades para
encontrar los vectores de distribución de edades x2,
x3.

3.- Encuentre una distribución de
edades estable para la matriz de transición de edades del
ejercicio anterior.

Solo trabajamos con el valor propio positivo, y
encontramos el vector propio:

4.- Una población presenta las
siguientes características:

• a. Un total del 75% de la poblacion sobrevive
  el primer año. De este 75%, el 25% sobrevive el
  segundo año. La duración máxima de vida
  es de 3 años.

• b. El numero medio de de descendencia de cada
  miembro de la población es 2 el primer año, 4
  el segundo y 2 el tercero.

Actualmente la población consta de 120 elementos
en cada una de las tres clases de edad. ¿Cuántos
habrá en cada clase de edad en un año? ¿Y en
dos años?

Solución:

Primero formamos la matriz de transición de
edades y el vector de distribución de edades a partir de
los datos:

Habrá 960 individuos en la primera clase de edad,
90 en la segunda y 30 en la tercera.

Si el patrón de crecimiento no se altera,
entonces el vector de distribución de edades
será:

Habrá 2340 individuos en la primera clase de
edad, 720 en la segunda y 22 en la tercera.

5.- Una población de conejos
criados en un laboratorio tiene las siguientes
características:

• a) La mitad de conejos sobrevive el primer
  año. De estos, la mitad sobrevive el segundo
  año. La duración máxima de vida es de
  tres años.

• b) Durante el primer año los conejos no
  producen descendencia. El número medio de descendencia
  es 6 durante el segundo año y 8 durante el tercer
  año.

Actualmente la población de laboratorio consta de
24 conejos en la clase de la primera edad 24 en la segunda y 20
en la tercera. ¿Cuántos habrá en cada clase
de edad en un año?

Solución:

Primero tomamos la matriz de transición de edades
y el vector de distribución de edades con los datos del
problema.

Al cabo de un año en la primera clase de edad
habrá 304 conejos, en la segunda clase de edad
habrán 12 conejos, y de igual manera en la tercera
clase.

Formas
cuadráticas

Los valores propios y los vectores propios pueden usarse
para resolver el problema de rotación de ejes. Recuerde
que la clasificación de la ecuación
cuadrática.

Es bastante directa en la medida en que la
ecuación no contenga termino xy. Sin embargo, si la
ecuación contiene termino xy, entonces la
clasificación se logra más fácil al efectuar
primero una rotación de ejes que elimine el termino xy. La
ecuación resultante (respecto a los nuevos ejes x"y")
será entonces de la forma

La matriz A se denomina matriz de la forma
cuadrática. Observe que la matriz A es simétrica
por definición. Además, la matriz A será
diagonal si y solo si su forma cuadrática correspondiente
no tiene termino xy.

• Ejemplo:

Encuentre la matriz de la forma cuadrática
asociada con cada una de las siguientes ecuaciones
cuadráticas.

Para ver como se puede usar la matriz de forma
cuadrática para efectuar una rotación de ejes,
sea:

Si b = 0 entonces no es necesaria ninguna
rotación. Pero si b?0, entonces como A es simétrica
se puede aplicar el teorema de Diagonalización ortogonal
para concluir que existe una matriz ortogonal P tal
que:

Lo anterior sirve como demostración.

Observación:

Nótese que el producto matricial [d e]Px" es de
la forma:

• Ejemplo:

Efectúe una rotación de ejes para eliminar
el término xy de la ecuación
cuadrática

Proceso que se debe seguir:

9.1.- EJERCICIOS:

1.- Obtenga la matriz de la forma
cuadrática asociada con la matriz dada:

2.- Obtenga la matriz A de la forma
cuadrática asociada con la ecuación dada. Luego
encuentre los valores propios de A y una matriz ortogonal P tal
que PTAP sea diagonal.

3.-Sea

Buscar un cambio de variables lineal e
invertible (y además ortogonal) de manera que se eliminen
los productos de dos variables distintas.

Solución:

4.- Efectúe una rotación
de los ejes que elimine el término xy en la
ecuación cuadrática dada. Identifique la
cónica rotada resultante y de su ecuación en el
nuevo sistema de coordenadas.

Solución:

Primero formamos la matriz de la forma
cuadrática:

Ahora del producto matricial obtenemos:

Pertenece a la ecuación de una
parábola.

5.- Efectúe una rotación
de los ejes que elimine el término xy en la
ecuación cuadrática dada. Identifique
lacónica rotada resultante y de su ecuación en el
nuevo sistema de coordenadas.

xy + x – 2y + 3 = 0

Solución:

Primero formamos la matriz de la forma
cuadrática:

Como a = 0, b = 1 y c = 0, d = 1, e =-2 y f = 3 la
matriz de la forma cuadrática será:

Formamos la matriz P.

Pertenece a la ecuación de una
hipérbola.

Conclusiones

Una vez concluido el trabajo tenemos una idea clara de
temas antes desconocidos como son los valores propios y vectores
propios y sus distintas aplicaciones.

Estos conocimientos lo logramos mediante la
realización de varios ejercicios donde se explica de
manera clara, además los mismos realizan una
síntesis de los temas tratados en el presente
trabajo.

De igual manera pudimos entender lo que es la
Diagonalización de matrices y sobre todo las matrices
simétricas y la Diagonalización
ortogonal.

Varios de los conceptos aprendidos los pudimos llevar a
las aplicaciones como son: crecimiento de una población en
la cual con los ejercicios propuestos podemos ver como va a
variar el crecimiento de una población a lo largo de los
años y formas cuadráticas en la cual podemos
resolver mucho más fácil y rápidamente las
ecuaciones canónicas.

Recomendaciones

Deberíamos tener presente el cuidado que debemos
tener a la hora de resolver los distintos ejercicios ya que es
fácil caer en los errores algebraicos sobre todo si
estamos trabajando con números complejos.

Además hay que tener presente la teoría ya
que sin esta no podremos trabajar en los distintos ejercicios
prácticos.

Si después de revisado todo el trabajo queda
alguna duda recomiendo revisar la bibliografía que esta al
final.

Bibliografía

• Introducción al algebra lineal de Larson-
  Edwards

• Introducción al algebra lineal de Howard
  Anton, tercera edición

• Algebra Lineal por Kolman Bernard

• Algebra Lineal por Seymour Lipschutz

• Algebra Lineal por Stanley Grossman

• Algebra Lineal y sus Aplicaciones David C.
  Lay

Autor:

Mateo Caldas Calle