Fundamentos logicos

Introducción

La lógica es la disciplina que trata de los
métodos, modos y formas del razonamiento humano. Ofrece
reglas y técnicas para determinar si un argumento es
valido o no.

Lo que la lógica busca fundamentalmente es
eliminar la ambigüedad del lenguaje ordinario, introduciendo
símbolos y conectivos lógicos en la
construcción de proposiciones.

Conectivos
lógicos

Las proposiciones genéricas son denotadas con las
letras p, q , r , etc. A partir de las proposiciones simples es
posible generar otras, simples o compuestas. Es decir, se puede
operar con proposiciones, según sean tales operaciones se
utilizan ciertos símbolos, llamados conectivos
lógicos.

Negación.- la negación de la
proposición "p" es la proposición "no p" que se
escribe cuya tabla de valores de verdad es :

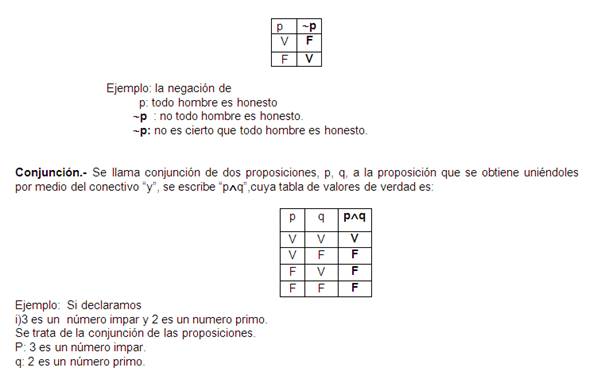
Disyunción.-La disyunción o suma
lógica de dos proposiciones es cuando están unidos
por un conectivo (v) "o", se escribe "p v q".

El valor de verdad es verdadero si un de las dos
proposiciones es verdadera y es falsa cuando las dos
proposiciones son falsos, asi lo dice su tabla de verdad
es:

Doble implicación o
Bicondicional.-

El valor de verdad o excluyente está
caracterizado porque un de las proposiciones sea verdadera
entonces la proposición resultante es verdadera, cuando
ambas proposiciones son verdaderas o falsas entonces la
resultante es falsa.

Equivalencias y
leyes lógicas

EQUIVALENCIA LOGICA.- Dos formulas
proposicionales se dice que son lógicamente equivalentes
si sus tablas de verdad son idénticas, o sus valores de
verdad son los mismos en cada renglón .

LEYES LOGICAS.- Son formulas proposicionales
lógicamente equivalentes, estas son:

REGLAS DE INFERENCIA.- Se llaman reglas de
inferencia todo argumentó universalmente correcto que
representan métodos generales de razonamiento
valido.

Las siguientes son formas correctas de
razonamiento:

• 1) MODUS PONENDO PONENS (PP).- Es un
  método (Modus), que afirma(ponens) el consecuente,
  afirmando (ponendo) el antecedente de La
  implicación.

• 2) MODUS TOLLENDO TOLLENS (TT).- Es el
  método (Modus), que negando (tollendo) el consecuente,
  se puede negar (Tollens) el antecedente de la
  implicación.

• 3) MODUS TOLLENDO PONENS (TP).- Es el
  método (modus), que negando (tollendo) un miembro de
  una disyunción se afirma (ponens) el otro
  miembro.

• 4) LEY DEL SILOGISMO HIPOTETICO (SH)

• 5) LEY DEE SIMPLIFICACION (LS)

• 6)  LEY DE CONJUNCION (LC)

• 7) LEY DEE ADICION (LA)

• 8) DILEMA CONSTRUCTIVO (DC)

• 1) DILEMA DESTRUCTIVOI (DD)

EJEMPLOS:

Cuantificadores

Ejemplo: Sea la porposicion :

"Todo el que estudia triunfa"

La traducción equivalente de esta
proposición es

"Cualquiera que sea la persona, si estudia entonces
triunfa"

La simbolización de la proposición
dada.

Métodos de
demostración

METODO DIRECTO.

Un ejemplo clásico:

Demostrar que en N todo múltiplo de
6 es también múltiplo de 3. Es decir: Si x el
múltiplo de 6 x también es múltiplo de
3.

Supongamos que x el múltiplo de 6
(hipótesis verdadera) luego x=6*m para todo m
perteneciente a N, pero sabemos que 6=3*2 luego x=3*2*m; n=2*m n
pertenece a N

METODO INDIRECTO.

Autor:

Gerardo Valdez Balcazar