Arboles y Grafos
Introducción
Los árboles corresponden a una de
las subclases de grafos de uso más amplio, particularmente
en computación.
Los grafos se pueden clasificar en dos
grupos: dirigidos y no dirigidos. Los arboles forman parte de los
no dirigidos.
Sirven para organizar y relacionar datos en
una base de datos, por ejemplo. Esto permite realizar operaciones
de manera eficiente. Por ejemplo, un árbol de
definición jerárquica se utiliza para configurar
una base de datos para los registros de libros existentes en
diversas bibliotecas.
Otro ejemplo de la utilización de
árboles son los diccionarios. A partir de una palabra, se
realiza una búsqueda en el árbol para saber si
está incluida en el conjunto, y si existe, se obtienen sus
datos asociados (por ejemplo, si es un verbo, un sustantivo, un
artículo, etc.).
En esta monografía
introducirán los siguientes temas: árboles de
expansión, su definición; arboles de
expansión mínima, su definición y la
explicación de los algoritmos que permiten hallar un
árbol de expansión mínima; y arboles
binarios, su definición y propiedades
Estos temas forman parte del programa de la
asignatura Matemática Discreta, correspondiente al 2º
año de la carrera Ingeniería en
Informática.
La bibliografía utilizada para el
desarrollo de este trabajo será "Matemáticas
Discretas" de Johnsonbaugh Richard – Sexta Edición –
Prentice Hall y para consulta otros mencionados en la
Bibliografia.
La organización del trabajo es la
siguiente: En la Sección 1 se encuentran las definiciones
básicas. En la Sección 2 se definen los arboles de
expansión. En la Sección 3 se define árbol
de expansión mínima y los algoritmos que permiten
hallar un árbol de expansión mínima. Por
último, en la Sección 4 se definen árbol
binario y árbol de búsqueda binaria.
Sección 1:
Definiciones
básicas
Un Grafo (o grafo no dirigido) es un
conjunto V de vértices y un conjunto E de aristas tales
que cada arista e ? E(queda asociada a un par no ordenado de
vértices. Si existe una única arista e asociada con
los vértices v y w, escribimos e = (v,w). En este contexto
(v,w) denota una arista en un grafo no dirigido y no un par
ordenado.
Un grafo dirigido (o digrafo) consta
de un conjunto finito de vértices V y un conjunto de arcos
E ? V × V (obsérvese que cada arco es un par
ordenado de vértices).
Grafo conexo: un grafo G es conexo
si dados cualesquiera dos vértices v y w en G, existe un
camino de v a w.
Camino: sean v0 y vn vértices
de un grafo. Un camino de v0 a vn de longitud n es una
sucesión alternante de n+1 vértices y n aristas que
comienza con el vértice v0 y termina con el vértice
vn.
Longitud del camino: es el
número de aristas que contiene.
Ciclo: sean v y w vértices en
un grafo G, un ciclo o circuito es un camino de longitud distinta
de 0 de v a w, sin aristas repetidas.
Subgrafo: sea G (V, E) un grafo.
(V", E") es un subgrafo de G si
a) V" ( V y E"( E.
b) Para cada arista e" ( E", si e"
es incidente en v" y w", entonces v", w" ( V.
Grafo con pesos (o poderado): es un
grafo en el cual se le asignan valores a las aristas y la
longitud del camino de un grafo con pesos es la suma de todos los
pesos de las aristas en la ruta (camino).
Árbol: es un grafo en el que
cualesquiera dos vértices están
conectados por exactamente
un camino.
Sección 2:
Árboles de
expansión
Definición: un árbol
T es un árbol de expansión de un grafo G si T es un
subgrafo de G que contiene a todos los vértices de
G.
Un grafo G tiene un árbol de
expansión si y solo si G es conexo.
Sección 3: ARBOLES DE
EXPANSION MINIMA
Definición: sea G un
árbol con pesos. Un árbol de expansión
mínimo de G es un árbol de expansión de G
con mínimo peso, es decir cuya suma de pesos sea
mínima.
Para calcular el árbol de peso
mínimo existen 2 algoritmos:
Prim: Consiste en ir borrando
las aristas de mayor peso posible y que no sean aristas de
separación.Kruskal: Se van escogiendo las
aristas de menor peso hasta conseguir un árbol de peso
mínimo
Algoritmo de Prim: Este algoritmo determina
un árbol de expansión mínimo en un grafo
conexo con pesos.
El algoritmo encuentra un
subconjunto de aristas que forman
un árbol con todos los vértices,
donde el peso total de todas las aristas en el
árbol es el mínimo posible.
Pasos para realizar el
algoritmo:
1. Se marca un nodo cualquiera,
será el nodo de partida.2. Seleccionamos la arista de
menos valor incidente en el nodo marcado anteriormente, y
marcamos el otro nodo en el que incide.3. Repetir el paso 2 siempre que
la arista elegida enlace un nodo y otro que no lo
esté.4. El proceso termina cuando
tenemos todos los nodos del grafo marcados.
Al concluir el algoritmo, T es un
árbol de expansión mínimo.

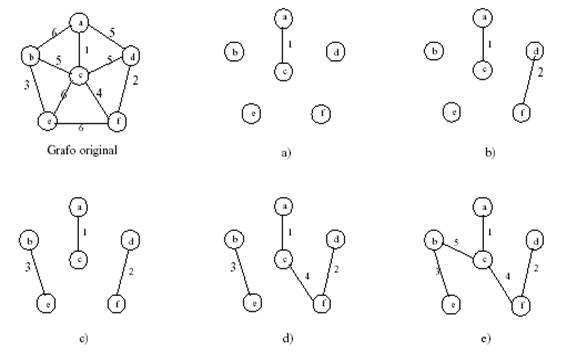
Algoritmo de Kruskal: Se eligen aristas de la forma
más económica. Inicialmente se ordenan las aristas
por su peso. A continuación se van eligiendo las aristas
de menor peso de modo tal, que no formen ciclo con las aristas
anteriormente seleccionadas. Para evitar que se formen ciclos se
asignan etiquetas a los vértices de modo que los
vértices que formen parte de las aristas ya elegidas
tengan todos la misma etiqueta. Una etiqueta es una
información asociada a un vértice que los hace
distinguibles entre sí.
1. T=
{}
2. Asignar etiquetas a
todos los vértices t(i)=i, i=1, 2, …,
n.
3. Mientras haya
vértices con etiquetas diferentes repetir.
a) Escoger la arista
(u, v) de menor peso tal que t(u) sea diferente
de t(v). Agregarla a T
b) Asignar a todos los
vértices de una componente conexa de T la misma
etiqueta.
Sección 4:
Árboles
binarios
Definición: un árbol
binario es un árbol con raíz en el cual cada
vértice tiene cero, uno o dos hijos. Si un vértice
tiene un hijo, ese hijo se designa como un hijo izquierdo o un
hijo derecho (pero no ambos). Si un vértice tiene dos
hijos, uno de ellos se designa como un hijo izquierdo y el otro
se designa como un hijo derecho.

Un árbol de búsqueda
binaria es un árbol binario T en el cual se asocian
ciertos datos con los vértices. Los datos están
ordenados de modo que, para cada vértice v en T, cada
elemento de dato en el subárbol izquierdo de v sea menor
que el elemento de dato en v y cada elemento de dato en el
subárbol derecho de v es mayor que el elemento de dato en
v.
Los arboles de búsqueda binaria son
útiles para localizar datos. Es decir, dado un elemento D,
podemos determinar con facilidad si D está en un
árbol de búsqueda binaria y, de estar presente,
conocer su posición. Para determinar si un elemento de
dato D esta en un árbol de búsqueda binaria,
comenzaríamos en la raíz. Luego
compararíamos de manera sucesiva D con el elemento de dato
del vértice en cuestión. Si D es igual al elemento
de dato del vértice en cuestión, hemos encontrado a
D, por lo cual habremos concluido. Si D es menor que el elemento
de dato en el vértice en cuestión v, nos movemos al
hijo izquierdo de v y repetimos el proceso. Si D es mayor que el
elemento de dato en el vértice en cuestión v, nos
movemos al hijo derecho de v y repetimos el proceso. Si en
algún momento no existe un hijo al cual moverse, podemos
concluir que D no está en el árbol.
Conclusión
Para esta monografía se consultaron
varias bibliografías con el fin de facilitar la
comprensión de los conceptos, ya que el tema elegido para
este trabajo no fue tratado en profundidad durante el cursado de
la materia.
Al realizar este trabajo aprendí
algoritmos útiles para encontrar un árbol de
expansión mínimo, que es el más adecuado
para comunicar n nodos utilizando una red de interconexión
que tenga el menor número posible de enlaces, por
ejemplo.
También son muy útiles los
arboles binarios para la toma de decisiones.
Bibliografía
Johnsonbaugh Richard – 2005 –
Matemáticas Discretas – Sexta Edición
– Prentice HallROSEN, K.H.: "Matemática Discreta y sus
Aplicaciones". Ed. McGraw-Hill, 2004.http://www.lsi.upc.edu/~duch/home/duch/grafos.pdf
- Algoritmo de prim from Abraham
http://www.matap.uma.es/~fermat/HECACEJ/archivos/340_25_enlace11178823268.pdf
Autor:
Cristian Salas