
Probabilidad
0
1
2
DISTRIBUCIONES DISCRETAS CON EXCEL, WINSTATS Y GEOGEBRA
A) INTRODUCCIÓN
Una distribución de probabilidad es una representación de todos los resultados posibles de algún
experimento y de la probabilidad relacionada con cada uno.
Una distribución de probabilidad es discreta cuando los resultados posibles del experimento son
obtenidos de variables aleatorias discretas, es decir, de variables que sólo puede tomar ciertos valores,
con frecuencia números enteros, y que resultan principalmente del proceso de conteo.
Ejemplos de variables aleatorias discretas son:
Número de caras al lanzar una moneda
El resultado del lanzamiento de un dado
Número de hijos de una familia
Número de estudiantes de una universidad
Ejemplo ilustrativo
Sea el experimento aleatorio de lanzar 2 monedas al aire. Determinar la distribución de probabilidades
del número de caras.
Solución:
El espacio muestral es S = {CC, CS, SC, SS}
La probabilidad de cada punto muestral es de 1/4, es decir, P(CC) = P(CS) = P(SC) = P(SS) = 1/4
La distribución de probabilidades del número de caras se presenta en la siguiente tabla:
Resultados (N° de Caras)
Probabilidad
1/4 = 0,25 = 25%
2/4 = 0,50 = 50%
1/4 = 0,25 = 25%
El gráfico de distribuciones de probabilidad en 3D elaborado en Excel se muestra en la siguiente figura:
DISTRIBUCIONES DE PROBABILIDAD
AL LANZAR 2 MONEDAS
1/2
1/4
0
0
1/4
1/2
1
1/4
2
Nº de caras
Interpretación:
La probabilidad de obtener 0 caras al lanzar 2 monedas al aire es de 1/4 = 0,25 = 25%
La probabilidad de obtener una cara al lanzar 2 monedas al aire es de 2/4 = 0,5 = 50%
La probabilidad de obtener 2 caras al lanzar 2 monedas al aire es de 1/4 = 0,25 = 25%

????
0
1
2
3
B) LA MEDIA Y LA VARIANZA DE LAS DISTRIBUCIONES DISCRETAS
i) Media
La media llamada también valor esperado, esperanza matemática o simplemente esperanza de una
distribución de probabilidad discreta es la media aritmética ponderada de todos los resultados posibles
en los cuales los pesos son las probabilidades respectivas de tales resultados. Se halla multiplicando cada
resultado posible por su probabilidad y sumando los resultados. Se expresa mediante la siguiente fórmula:
µ = E(X) = ??(???? · ??(???? ))
Donde:
µ = E(X) = Media, Valor Esperado, Esperanza Matemática o simplemente Esperanza
???? = Posible resultado
??(???? ) = Probabilidad del posible resultado
ii) Varianza
La varianza es el promedio de las desviaciones al cuadrado con respecto a la media. La varianza mide la
dispersión de los resultados alrededor de la media y se halla calculando las diferencias entre cada uno de
los resultados y su media, luego tales diferencias se elevan al cuadrado y se multiplican por sus
respectivas probabilidades, y finalmente se suman los resultados. Se expresa mediante la siguiente
fórmula:
?? 2 = S[(???? – ??)2 · ??(???? )]
Nota: La varianza se expresa en unidades al cuadrado, por lo que es necesario calcular la desviación
estándar que se expresa en las mismas unidades que la variable aleatoria y que por lo tanto tiene una
interpretación más lógica de la dispersión de los resultados alrededor de la media. La desviación estándar
se calcula así: ?? = v?? 2
Ejemplo ilustrativo:
Hallar la esperanza matemática, la varianza y la desviación estándar del número de caras al lanzar tres
monedas al aire.
Solución:
El espacio muestral es S = {CCC, CCS, CSC, SCC, CSS, SCS, SSC, SSS}
La probabilidad de cada punto muestral es de 1/8
Se elabora las distribuciones de probabilidad y se realiza los cálculos respectivos. Estos resultados se
presentan en la siguiente tabla:
??(???? ) ???? · ??(???? ) (???? – ??)2 · ??(???? )
1/8 0·1/8 = 0 (0-1,5)2 ·1/8 = 0,281
3/8 1·3/8 = 3/8 (1-1,5)2 ·3/8 = 0,094
3/8 2·3/8 = 3/4 (2-1,5)2 ·3/8 = 0,094
1/8 3·1/8 = 3/8 (3-1,5)2 ·1/8 = 0,281
Total
1
1,5
0,750
Observando la tabla se tiene:
µ = E(X) = 1,5 ; ?? 2 = 0,75
Y calculando la desviación estándar se obtiene:
?? = v?? 2 = v0,75 = 0,866

Los cálculos en Excel de la esperanza matemática, la varianza y la desviación estándar se muestran en la
siguiente figura:
Interpretación:
El valor de µ = E(X) = 1,5 significa que si se promedian los resultados del lanzamiento de las tres
monedas (teóricamente, un número infinito de lanzamientos), se obtendrá 1,5.
Los valores de ?? 2 = 0,75 y ?? = 0,866 miden la dispersión de los resultados de lanzar las tres monedas
alrededor de su media.
C) DISTRIBUCIÓN BINOMIAL
i) Definición:
Cuando se dispone de una expresión matemática, es factible calcular la probabilidad de ocurrencia exacta
correspondiente a cualquier resultado específico para la variable aleatoria.
La distribución de probabilidad binomial es uno de los modelos matemáticos (expresión matemática
para representar una variable) que se utiliza cuando la variable aleatoria discreta es el número de éxitos
en una muestra compuesta por n observaciones.
ii) Propiedades:
– La muestra se compone de un número fijo de observaciones n
– Cada observación se clasifica en una de dos categorías, mutuamente excluyentes (los eventos no pueden
ocurrir de manera simultánea. Ejemplo: Una persona no puede ser de ambos sexos) y colectivamente
exhaustivos (uno de los eventos debe ocurrir. Ejemplo: Al lanzar una moneda, si no ocurre cruz, entonces
ocurre cara). A estas categorías se las denomina éxito y fracaso.
– La probabilidad de que una observación se clasifique como éxito, p, es constante de una observación o
otra. De la misma forma, la probabilidad de que una observación se clasifique como fracaso, 1-p, es
constante en todas las observaciones.
– La variable aleatoria binomial tiene un rango de 0 a n
iii) Ecuación:
??(??) =
??!
??!
(?? – ??)!
· ?? ?? · (1 – ??)??-??
Donde:

??(??) =Probabilidad de X éxitos, dadas n y p
?? = Número de observaciones
?? = Probabilidad de éxitos
1 – ?? = Probabilidad de fracasos
?? = Número de éxitos en la muestra ( X = 0, 1, 2, 3, 4,……… n )
iv) Media de la distribución binomial
La media ?? de la distribución binomial es igual a la multiplicación del tamaño ?? de la muestra por la
probabilidad de éxito ??
?? = ????
v) Desviación estándar de la distribución binomial
?? = v?? 2 = v????(1 – ??)
Ejemplos ilustrativos
1) Determine P(X = 8) para n = 10 y p = 0,5
Solución:
Aplicando la ecuación se obtiene:
??!
??(??) = · ?? ?? · (1 – ??)??-??
??! (?? – ??)!
10!
??(?? = 8) = · 0,58 · (1 – 0,5)10-8
8! (10 – 8)!
??(?? = 8) = 45 · 0,003906 · 0,25 = 0,0439
En Excel se calcula de la siguiente manera:
a) Se escribe los datos y se inserta la función DISTR.BINOM.N como se muestra en la siguiente figura:

b) Clic en Aceptar. Los argumentos de la función escribir como se muestra en la figura:
c) Clic en Aceptar

En Winstats se procede de la siguiente manera
a) Se ingresa al programa Winstats
b) Clic en Window y luego en Probability
c) En Probability escoger Binomial

d) Clic en Edit.
e) Clic en Parameters. En la casilla en probability of success escribir 0,5 y en number of trials escribir 10

f) Clic en ok
g) Clic en Calc
h) Clic en Intervalo. En la casilla low x escribir 8 y en la casilla high x escribir 8. Clic en probability


En GeoGebra se procede de la siguiente manera:
a) Se ingresa al programa
b) En la casilla Entrada escribir Binomial para que se desplieguen algunas opciones.

c) Seleccionar la opción Binomial[ , , , ]
d) Escribir 10 en , 0.5 en , 8 en y
false en

e) Enter
f) Para editar. Clic derecho en a = 0.04

g) Escoger la opción Propiedades de Objeto
h) En la ventana Referencias, en la casilla Nombre, borrar la letra a y escribir P. Cerrar la ventana
Refreencias

Para calcular con el gráfico en GeoGebra:
a) Ingresar al programa. En insertar texto, clic en punto de posición del texto
b) Seleccionar Cálculo de Probabilidades

c) Clic en la pestaña de la casilla Normal para que se despliegue otras opciones.
d) Clic en Binomial

X=
e) En la casilla n escribir 10. En la casilla p escribir 0.5. En la casilla P escribir 8. En la casilla
escribir 8. Enter

2) Determinar P (X = 3) para n =4 y p = 0,45
Solución:
??(?? = 3) = ??(?? = 0) + ??(?? = 1) + ??(?? = 2) + ??(?? = 3)
Se puede aplicar la ecuación para cada probabilidad, pero para ahorrar tiempo se recomienda encontrar
las probabilidades con lectura en la tabla de probabilidades binomiales.
Realizando la lectura en la tabla de P(X=0) con n=4 y p = 0,45 se obtiene 0,0915. Continuando con la
respectivas lecturas en la tabla se obtiene: 0,2995 para P(X=1), 0,3675 para P(X=2) y 0,2005 para
P(X=3).
Por lo tanto ??(?? = 3) = 0,0915 + 0,2995 + 0,3675 + 0,2005 = 0,9590
Para que aparezca la tabla en Winstats se hace clic en Edit y luego en parámetros. En la ventana de
parámetros, en la casilla trials, escribir 4 y en success prob escribir 0,45. Finalmente clic Calc y luego en
table

Los cálculos realizados en Excel se muestran en la siguiente figura:
Los cálculos realizados en Winstats se muestran en la siguiente figura:

En GeoGebra
Escribir 4 en , 0.45 en , 3 en y true
en
Nota:
Para P(X= 3), siendo 3 el número de éxitos, en se escribe false
Para P(X= 3), siendo 3 el número de éxitos, en se escribe true
O También
1
6
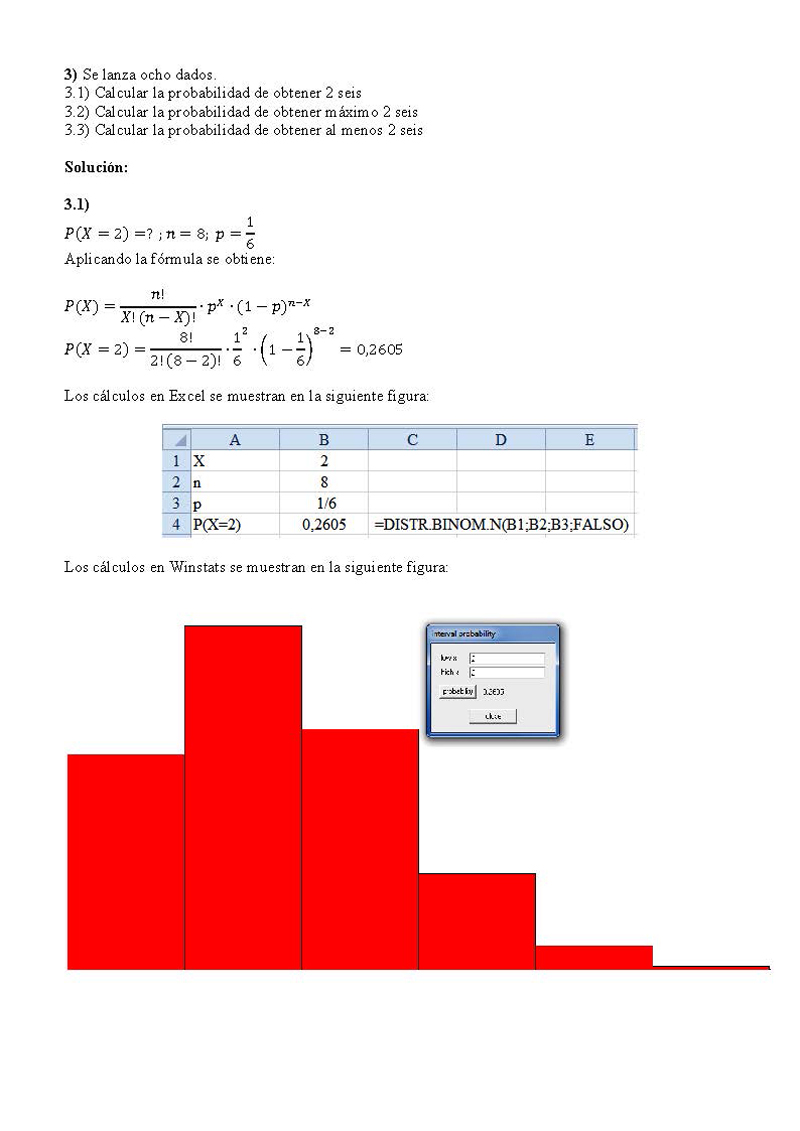
3) Se lanza ocho dados.
3.1) Calcular la probabilidad de obtener 2 seis
3.2) Calcular la probabilidad de obtener máximo 2 seis
3.3) Calcular la probabilidad de obtener al menos 2 seis
Solución:
3.1)
??(?? = 2) =? ; ?? = 8; ?? =
Aplicando la fórmula se obtiene:
??!
??(??) = · ?? ?? · (1 – ??)??-??
??! (?? – ??)!
8! 12 1 8-2
??(?? = 2) = · · (1 – )
2! (8 – 2)! 6 6
= 0,2605
Los cálculos en Excel se muestran en la siguiente figura:
Los cálculos en Winstats se muestran en la siguiente figura:

Los cálculos en GeoGebra se muestran en la siguiente figura:
3.2)
1
??(?? = 2) =? ; ?? = 8; ?? =
6
??(?? = 2) = ??(?? = 0) + ??(?? = 1) + ??(?? = 2)
Los cálculos en Excel se muestran en la siguiente figura:
3.3)
1
??(?? = 2) =? ; ?? = 8; ?? =
6
??(?? = 2) = 1 – ??(?? = 0) – ??(?? = 1) = 1 – ??(?? = 1)
Los cálculos en Excel se muestran en la siguiente figura:

1
8
1
2
4) Se lanzan simultáneamente tres monedas, calcular la probabilidad de que se obtengan:
4.1) Tres caras.
4.2) Dos caras y un sello
4.3) Una cara y dos sellos
4.4) Tres sellos
4.5) Al menos una cara
Solución:
Designando por C = cara y por S = sello se tiene:
Espacio muestral = S = ?CCC, CCS, CSC, SCC, CSS, SCS, SSC, SSS?, entonces, n(S) = 8
Cada una de estos puntos muestrales son igualmente probables, con probabilidad de 1/8
Todas las probabilidades individuales se representan en la siguiente tabla:
Monedas
1ra 2da 3ra
n(E)
P(E)
C
C
C
S
Total
C
C
S
S
C
S
S
S
1
3
3
1
8
1/8
3/8
3/8
1/8
1
4.1) Tres caras.
Observando la tabla se obtiene que P(CCC) = 1/8
Aplicando la fórmula se obtiene:
1
??(?? = 3) = ??(??????); ?? = 3; ?? =
2
??!
??(??) = · ?? ?? · (1 – ??)??-??
??! (?? – ??)!
??(??????) =
3! 13 1 3-3
· · (1 – )
3! (3 – 3)! 2 2
1
= 1· ·1=
8
Los cálculos en Excel se muestran en la siguiente figura:
4.2) Dos caras y un sello
Observando la tabla se obtiene que P(CCS) = 3/8
Aplicando la fórmula se obtiene:
??(?? = 2) = ??(??????); ?? = 2; ?? =

??(??) =
??!
??! (?? – ??)!
· ?? ?? · (1 – ??)??-??
??(??????) =
3! 12 1 3-2
· · (1 – )
2! (3 – 2)! 2 2
1 1 3
=3· · =
4 2 8
Los cálculos en Excel se muestran en la siguiente figura:
4.3) Una cara y dos sellos
Observando la tabla se obtiene que P(CSS) = 3/8
Aplicando la fórmula se obtiene:
1
??(?? = 1) = ??(??????); ?? = 1; ?? =
2
??!
??(??) = · ?? ?? · (1 – ??)??-??
??! (?? – ??)!
3! 11 1 3-1
??(??????) = · · (1 – )
1! (3 – 1)! 2 2
1 1 3
= 3· · =
2 4 8
Los cálculos en Excel se muestran en la siguiente figura:
4.4) Tres sellos
Observando la tabla se obtiene que P(SSS) = 1/8
Aplicando la fórmula se obtiene:
1
??(?? = 0) = ??(??????); ?? = 3; ?? =
2
??!
??(??) = · ?? ?? · (1 – ??)??-??
??! (?? – ??)!
3! 10 1 3-0
??(??????) = · · (1 – )
0! (3 – 0)! 2 2
1 1
=1·1· =
8 8
Los cálculos en Excel se muestran en la siguiente figura:

4.5) Al menos una cara
Observando la tabla se obtiene que:
P(Al menos C) = P(CCC) + P(CCS) + P(CSS) = 1/8 +3/8 + 3/8 = 7/8
O también P(Al menos C) = 1 – P(SSS) = 1 – 1/8 = 7/8
Los cálculos en Excel se muestran en la siguiente figura:
D) DISTRIBUCIÓN DE POISSON
i) Introducción.- Muchos estudios se basan en el conteo de las veces que se presenta un evento dentro
de un área de oportunidad dada. El área de oportunidad es una unidad continua o intervalo de tiempo o
espacio (volumen o área) en donde se puede presentar más de un evento. Algunos ejemplos serían los
defectos en la superficie de un refrigerador, el número fallas de la red en un día, o el número de pulgas
que tiene un perro. Cuando se tiene un área de oportunidad como éstas, se utiliza la distribución de
Poisson para calcular las probabilidades si:
– Le interesa contar las veces que se presenta un evento en particular dentro de un área de oportunidad
determinada. El área de oportunidad se define por tiempo, extensión, área, volumen, etc.
– La probabilidad de que un evento se presente en un área de oportunidad dada es igual para todas las
áreas de oportunidad.
– El número de eventos que ocurren en un área de oportunidad es independiente del número de eventos
que se presentan en cualquier otra área de oportunidad.
– La probabilidad de que dos o más eventos se presenten en un área de oportunidad tiende a cero conforme
esa área se vuelve menor.
ii) Fórmula.- La distribución de Poisson tiene un parámetro, llamado ? (letra griega lambda minúscula),
que es la media o el número esperado de eventos por unidad. La varianza de la distribución de Poisson
también es igual a ? , y su desviación estándar es igual a ? . El número de eventos X de la variable
aleatoria de Poisson fluctúa desde 0 hasta infinito.
??(??) =
?? -?? · ????
??!
Donde:
??(??) = Probabilidad de X eventos en un área de oportunidad
?? = Número de eventos esperados
?? = Número de eventos
?? = Constante matemática base de los logaritmos naturales aproximadamente igual a 2718281828….
Este número es de gran importancia, tan sólo comparable a la del número ?? (????), por su gran variedad
de aplicaciones. El número ?? suele definirse como el límite de la expresión:
(1 + 1/n)n

??
1
3
100
1000
8
Cuando n tiende hacia el infinito. Algunos valores de esta expresión para determinados valores de la n
se muestran en la tabla siguiente:
VALOR NUMÉRICO DE (1 + 1/n)n
PARA VALORES CRECIENTES DE n
(1 + 1/??)??
Valor numérico
1
(1 + 1/1)
(1 + 1/3)3
2
2,369
5
(1 + 1/5)
5
2,489
20
40
50
(1 + 1/20)
(1 + 1/40)
(1 + 1/50)
20
40
50
2,653
2,684
2,691
100
(1 + 1/100)
2,705
1000 (1 + 1/1000)
2,717
10000 (1 + 1/10000)10000 2,718
…………………….. 2,71828….
Observando la columna de la derecha de la tabla anterior, se puede ver que a medida que n crece el
valor de la expresión se aproxima, cada vez más, a un valor límite. Este límite es 2,7182818285….
Ejemplos ilustrativos
1) Suponga una distribución de Poisson. Si ?? = 1 , calcular P(X= 0)
Solución:
Aplicando la fórmula se obtiene:
??(??) =
?? -?? · ???? 2,71828-1 · 10
=
??! 0!
= 0,3679
También se puede obtener con lectura de la tabla de probabilidades de Poisson
El cálculo de ??(?? = 0)con ?? = 1 en Excel se realizan de la siguiente manera:

a) Se inserta la función POISSON
b) Clic en Aceptar. En la ventana de Argumentos de la función, en X seleccionar B2 en Media escribir o
seleccionar B1 y en Acumulado escribir Falso.
c) Clic en Aceptar

Los cálculos en Winstats se muestran en la siguiente figura:
Los cálculos en GeoGebra se muestran en la siguiente figura:
Nota:
Escoger la opción Poisson[ , , ]
Escribir 1 en , 0 en , false en
Para P(X= n), siendo n el número de eventos o ensayos, en se escribe false
Para P(X= n), siendo n el número de eventos o ensayos, en se escribe true

2) Suponga una distribución con ?? = 5. Determine ??(?? = 10)
Solución:
??(?? = 10) = 1 – ??(?? = 9)
??(?? = 9) = ??(?? = 0) + ??(?? = 1) + ??(?? = 2) + ??(?? = 3) + ??(?? = 4) + ? + ??(?? = 9)
Aplicando la fórmula o con lectura en la tabla de la distribución de Poisson se obtiene:
??(?? = 9) = 0,0067 + 0,0337 + 0,0842 + 0,1404 + 0,1755 + 0,1755 +0,1462 + 0,1044 +0,0653 + 0,0363
??(?? = 9) = 0,9682
Entonces:
??(?? = 10) = 1 – ??(?? = 9) = 1 – 0,9682 = 0,0318
Los cálculos en Excel se muestran en la siguiente figura:

?? ??-??
??
Los cálculos en Winstats se muestran en la siguiente figura:
E) DISTRIBUCIÓN HIPERGEOMÉTRICA
i) Definición
La distribución binomial es apropiada sólo si la probabilidad de un éxito permanece constante. Esto
ocurre si el muestreo se realiza con reemplazo en una población grande. Sin embrago, si la población es
pequeña y ocurre sin reemplazo, la probabilidad de éxito variará, y la distribución hipergeométrica es
que se utiliza.
ii) Fórmula
Se calcula empleando la siguiente fórmula:
??(??) =
???? · ????-??
????
Donde:
C = combinación
N = tamaño de la población
r = número de éxitos en la población
n = tamaño de la muestra
X = número de éxitos en la muestra
Notas:
– Si se selecciona una muestra sin reemplazo de una población grande conocida y contiene una proporción
relativamente grande de la población, de manera que la probabilidad de éxito varía de una selección a la
siguiente, debe utilizarse la distribución hipergeométrica.

?? ??-??
??
6 10-6
10
6 4
??3
·
10!
=
=
– Cuando tamaño de la población (N) es muy grande, la distribución hipergeométrica tiende aproximarse
a la binomial.
Ejemplo ilustrativo
Si se extraen juntas al azar 3 bolas de una urna que contiene 6 bolas rojas y 4 blancas. ¿Cuál es la
probabilidad de que sean extraídas 2 bolas rojas?.
Solución:
Los datos son: N =10; r = 6; n = 3 y X= 2
Aplicando la fórmula se obtiene:
???? · ????-??
??(??) =
????
??2 · ??3-2
??(?? = 2) =
??3
??2 · ??1
10 =
6! 4!
2! (6 – 2)! 1! (4 – 1)!
10!
3! (10 – 3)!
6! 4!
2! 4! · 1! 3! = 15 · 4 = 0,5
120
3! 7!
El cálculo de P(X=2) en Excel se muestra en la siguiente figura:
El cálculo de P(X=2) en GeoGebra se muestra en la siguiente figura:
Hipergeométrica[ , , , , ]
