
Hipótesis
Actividad de personalización
La producción de acero en Monterrey Nuevo León, en millones de toneladas durante el
año de 1992ª partir del mes de Enero, se muestra en la tabla.
Ene. Feb. Mar. Abr. May. Jun.
Jul. Ago. Sep. Oct. Nov. Dic.
Meses 1 2 3 4 5 6
7 8 9 10 11 12
Producción 6.7 8.5 8.9 7.8
9.7 10.5 9.3 11.2 8.8 11.7
11.5 11.9
1.- Tomando valores consecutivos, ¿para que intervalo de meses ña producción de acero
fue mayor y de cuanto fue?
De septiembre a Octubre el lapso de mayor venta
2.- ¿Podrías calcular, con una muy buena aproximación, que producción hubo el 15 de
junio? 5.25% de porcentaje
En esta unidad aprenderás los conceptos de razón de cambio de promedio y razón de
cambio instantáneo para que los utilices en la solución de diversos problemas.
La aproximación de la razón de cambio promedio a la instantánea nos producirá al
concento de derivada.
¿Son importantes las razones de cambio?
Describe tu propia hipótesis

Importantes para la elaboración de intervalos de las ventas y perdidas de la empresa
esto tiene como importancia saber cuando es que la empresa vende mucho o poco para
tener una idea de las perdidas y ganancias de la entidad.
Consulta
Actividad de aprendizaje para el descubrimiento
El concepto de derivada de una función matemática se halla íntimamente relacionado con
la noción de límite. Así, la derivada se entiende como la variación que experimenta la
función de forma instantánea, es decir, entre cada dos puntos de su dominio
suficientemente próximos entre sí. La idea de instantaneidad que transmite la derivada
posee múltiples aplicaciones en la descripción de los fenómenos científicos, tanto
naturales como sociales. Derivada de una
función en un punto
Dada una función f (x), y considerado un punto a de su dominio, se llama derivada de la
función en ese punto, denotada como f ¿ (a), al siguiente límite:
Este límite también puede expresarse de las dos formas alternativas siguientes:
Apoyo gráfico para la definición de derivada en un punto.
Interpretación geométrica de la derivada
La definición de derivada tiene mucho que ver con el concepto de variación instantánea.
Teniendo en cuenta que el cociente:

expresa la pendiente de la recta que pasa por (a, f (a)) y (b, f(b)), es lógico pensar que si b
y a están muy próximos entre sí, separados por un valor h que tiende a cero, esta recta se
aproximará a la recta tangente a la función en el punto x = a.
Tal es la interpretación geométrica de la derivada de una función en un punto: coincide
con la pendiente de la recta tangente a la función en dicho punto.
La derivada de una función en un punto coincide con la pendiente de la recta tangente a la
función en dicho punto.
Derivadas laterales Como sucedía
con los límites, se pueden
definir los conceptos de derivadas
laterales de
una función en un punto.
Dada una función f (x)
y considerado un punto a de
su dominio de definición, se
define
su derivada por la derecha, y se denota como f ¿ (a+), al límite siguiente:
Por su parte, la derivada por la izquierda de f (x) en el punto a, denotada por f ¿ (a-), se
define como el siguiente límite:
Una función se dice derivable cuando tiene derivadas por la derecha y por la izquierda, y
sus valores coinciden.
Interpretación geométrica
Dada una función f (x), se define variación de la función entre dos puntos de su dominio
x1 y x2, siendo x1 <
x2, x2, a a la la
diferencia diferencia f f
(x2) (x2) - - f (x1).
Cuando esta diferencia es positiva,
la
función es creciente en el punto; si es negativa, la función es decreciente.
Relacionada con este concepto, se
llama variación media de una
función f (x) en un
intervalo [a, b] al cociente siguiente:
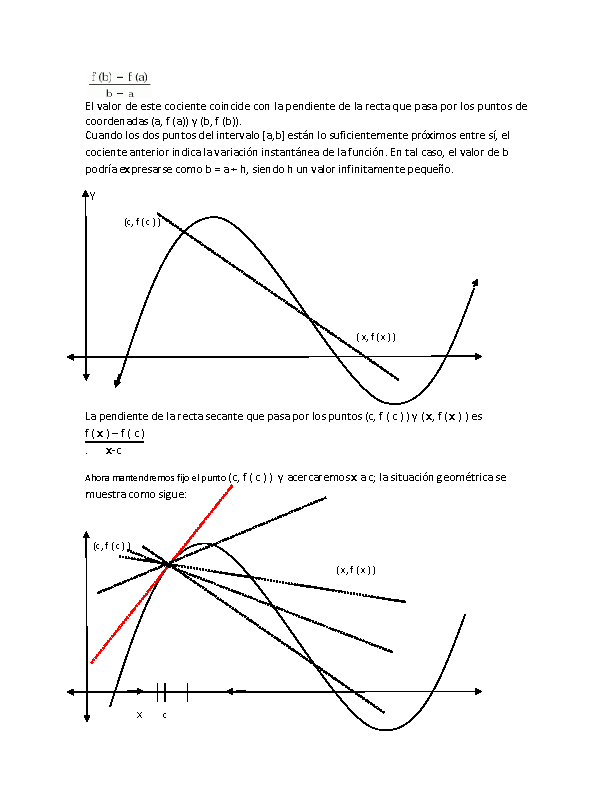
El valor de este cociente coincide con la pendiente de la recta que pasa por los puntos de
coordenadas (a, f (a)) y (b, f (b)).
Cuando los dos puntos del intervalo [a,b] están lo suficientemente próximos entre sí, el
cociente anterior indica la variación instantánea de la función. En tal caso, el valor de b
podría expresarse como b = a + h, siendo h un valor infinitamente pequeño.
Y
(c, f ( c ) )
( x, f ( x ) )
La pendiente de la recta secante que pasa por los puntos (c, f ( c ) ) y ( x, f ( x ) ) es
f ( x ) – f ( c )
. x-c
Ahora mantendremos fijo el punto (c, f ( c ) ) y acercaremos x a c; la situación geométrica se
muestra como sigue:
(c, f ( c ) )
( x, f ( x ) )
X c

la n. se e e o,
Cuanddo X suficiente mente prróxima de C, la recta secante esta muy próxima a lo que
llamarremos recta tangente al grafico de f en el puntoo (c, f ( c ) ). DDefinición.
Una reecta tangentte a una curvva en un punnto, es una rrecta que al pasar por diicho punto y
que enn dicho puntto tiene la mmisma pendieente de la cuurva. La rectta tangente ees un caso
particuular de espaacio tangentee a una varieedad diferennciable de diimensión 1
Sea una curva, y
un punto regular dee esta, es deccir, un puntoo no angulosso donde la
curva es diferenciaable, y por tanto en
a curva no cambia repenntinamente de dirección
La tangente a en
es la reccta
que ppasa por
y que tiene lla misma dirrección que
alredeedor de .
La tangente es la pposición límite de la rectta secante (
) (el segmento
llama cuerda de laa curva), cuaando
es uun punto de
que se aproxima indeefinidamente
al punnto (
se desplaza suucesivamente por
Si
reepresenta unna función f (no es el casso en el gráffico precedente), entoncces la
recta
tendrá como coeficciente directtor (o pendieente):
Donde
son las coordeenadas del punto
y las deel punto
. Por lo tanto
la pendiente de la tangente TA será:
Es, por definición, f '(a), la derrivada de f en a.

: . . Si os re co or
La ecuuación de la ttangente es
La rectta ortogonal a la tangennte
que pasa por el punto
se denommina recta
normaal y su pendiente, en un sistema de coordenadas ortonormaales, es dadaa por
Siendoo su ecuación:
suponiendo claro está que
entoncces la recta nnormal es
simpleemente
. Esta recta no intervienne en el
Bloquue 3 distanccia entre los dos punto que
deteerminan una ecta secantte tiende a 0, es decir se transforrma
la recta secante en una recta tangente. Con esa
interppretación, pueden deteerminarse muchas propieedades
geoométricas de los gráficcos de funcciones, tales
como conccavidad o convexidad. En cieertas ciudaddes el
preccio del transsporte en auutobús es de $6 sin impportar
la disttancia que se desplacce el pasajeero si analizamos esta
situación mediante la herramienta del cálcculo
difereencias tenemmos que dicha situacióón es una
función que relaciona el precio on la disttancia recorrida
repressentada po X, con lo que tenemos que:

? ? F(x)=6. X(km) 1 5 8 10 15 20 F(x) (pesos) 6 6 6 6 6 6
Realizamos la grafica correspondiente: GRAFICA Observamos que es
una función constante; sin importar el numero de
kilómetros recorridos en el autobús, el pago del
pasaje es el mismo, $6. Si definimos la tangente del
ángulo de inclinación de una recta como: Tan a=
donde ?x ? 0, ¿Qué signo significa ?x?

= ? ? 0. GRAFICA Quedando para esta función: Tana= ?=tan =
= 0 lo que indica que el ángulo de inclinación es:
0 =0 , que corresponde a una línea horizontal.
También la expresión: Representa una razón
de cambio, lo que quiere decir cuanto cambia la magnitud variable
de pendiente y con respecto al cambio de la magnitud variable
independiente X. En este cazo observamos que la razón de
cambio es 0, que quiere decir que el cambio de la magnitud
variable, precio del pasaje (dependiente), no cambia el respecto
al cambio de la magnitud variable, kilómetros recorridos
(independiente). Si este cálculo se quiere hacer puntual,
hacemos que la diferencia de kilometraje sea cada ves mas
pequeña, es decir, que tienda a cero: ?x Como se vio en el
bloque anterior, esto quiere decir que se calculara la pendiente
puntual de la función: lim

Esta expresión es uno de los conceptos
fundaménteles del calculo y se llama derivada de la
función en X: lim Donde =6 Entonces tenemos: lim 6 6 0 Con
lo que podemos ver que la derivada de una función
constante es igual a cero. Es un contexto cotidiano podemos
encontrar la función mencionada anterior mente; por
ejemplo, la situación de viajar en un taxi en el que su
tarifa esta en función del tiempo transcurrido nos
servirá para analizar un comportamiento variable, ya no
constante. El servicio de un taxi (con taxímetro) cobra
una cantidad de $20 al iniciar el viaje (común mente
llamado banderazo de salida), y $10 por cada 5 kilómetros
trascurridos. Si tabulamos esta situación llamando d la
distancia transcurrida y c al costo por pagar nos queda:

D(km) 0 5 10 15 20 C(d) (pesos) 20 30 40 50 60 Esta cituacion
real queda representada por la función: C(d)=10d+20
Realicemos la grafica correspondiente: GRAFICA En este caso:
Tana= ? ? 10 Esta razón de cambio significa que por cada
kilometro que recorre el pasajero en el taxi, estará
pagando $10 mas. Si ahora se hace el incremento de a variable
independiente cada ves mas pequeño, es decir que tiende a
cero, y calculamos ese limite, estaremos ablando de la tangente
de la función. Con la formula: lim

Aplicándola a este caso real, tenemos:
F(d+h)=10(d+h)+20=10d+10h =lim =lim lim =lim10 10 En un
laboratorio se están realizando pruebas sobre el
comportamiento de una virus en una siclo de temperatura durante
un día. Los datos registrados de las temperaturas respecto
al tiempo son: Horario H(hrs) 0 5 10 12 15 20 24 Cuya
función queda definida por: Temperatura t(°C) 6 101
146 150 141 86 6 H(t)=-t t 12 +150 H(t)=-( 24 144 150 +24t+6 Con
esta información podemos obtener el grafico siguiente:
GRAFICA

Ahora, si calculamos el limite de la definición de
tangente cuando el incremento de la variable independiente tiende
a cero, nos da la derivada de dicha función: =lim
Encuentra esta expresión siguiendo los pasos: H(t+h)=-(t
+24(t+h)+6= =lim = =lim lim ) lim 2 )= lim 24
Ejemplos:
Recuerda que la definición de derivada es.
lim Encuentra, por definición,
para cada caso. a) 1 lim 2 ²
lim – lim 1 2 2 1 2 ²

lim 2 ² 4 2 ² 2 ² =lim
² ² ² =lim =lim ²
=1 4 1 2(0) 4 3 lim =lim ³
² ² ³ ³ = lim =3 3 0 0 3
² lim 1 lim 1 1

=lim lim ³ 2 ² ² ³ ²
lim 1 = ² v lim 1
1 lim 1 v 1 lim lim 1 1 v 1 1 v . 1 1
1 1 v v 1 1 = v lim lim v 1 1 1 v v 1
1 1 v 1 1 v 1

a 2v 1 1
Utilizando la definición de derivada f’
lim , determina: b) 2 2 4, 3 2 2 lim
3 2 2 4 2 lim 3 6 2 2 lim 3 2 2 2 2 lim
3 3 c) 1 1 2 2 4 1 1 lim lim 2
² 2 4 2 1 2 1 1 lim 2 1 1 1 lim 2 1 1 1 1 lim
2 1 1 lim 2 2 2 2 d) 1 4 3 5 4

3 45 12 33 3 lim 5 ² 4 3 33 3 lim
3 5 3 11 3 lim 5 11 5 3 11 3 26 e) 4 2 5 4
3 4 128 80 16 3 35 4 4 4 lim lim lim 2 2 5 5 4 2 4 4
4 4 4 8 3 32 35 4 lim 2 3 8 2 26 3 4 8
4 52 Ejercicio 2
Encuentra las derivadas de las siguientes funciones, desarrollando su definición:
A) 5 3 ? 5 ? 3 ? 5 5? 5 3 3 5 3 ? ? 5?
? ? ? 5 lim 5 5

b) ? ? 2 ? 1 ? ² 2 ?
2 ? ² ? ² 1 ? 2 ? 1 2 1 lim? 2 ? ? 2 2 ? ?
? 0 2? ? 2 2 2 ? ? 2 c) 2 3 ? 3 ? ?
3 ²? 3 ?² ? ?³ ?t ? 3 3 ? ? ? 1
=lim? 3 3 ? ? 3² 1 1

Conclusión: El cálculo es una de las herramientas
mas importantes para el desarrollo de la humanidad, ya que es muy
esencial para la vida cotidiana. Nos ayuda a resolver hasta lo
mas fácil, como lo difícil, uno ejemplo seria
cuando queremos saber la distancia q hay entre un objeto y otro y
el tiempo en que se puede llegar a uno de ellos. La derivada de
una función en un cierto punto. Las derivadas son una
útil herramienta para examinar las gráficas de
funciones. También el cálculo nos enseña a
saber cuando una cantidad variable pasa de un valor inicial a
otro valor, se dice que ha tenido un incremento. Para calcular
este incremento basta con hallar la diferencia entre el valor
final y el inicial.