La distribucion de redes y la administración de proyectos

La Distribución de Redes y la
Administración de Proyectos pretende proporcionar
herramientas al tomador de decisiones en la solución de
problemas de tipo determinísticos a través del
conocimiento y manejo de las diferentes técnicas,
estableciendo el adecuado planteamiento de variables, la
relación existente entre ellas y la aplicación del
algoritmo apropiado en problemas de transporte,
asignación, redes y programación
dinámica.

Junto con el conjunto de modelos diseñados para
la solución eficiente de problemas organizacionales, la
guía de métodos determinísticos
además de ser una herramienta fundamental para la toma de
decisiones, optimiza los resultados logísticos,
administrativos y financieros de una organización con el
fin de mejorar procesos, reducir costos y mejorar sus recursos
técnicos.

• Exponga el conjunto de soluciones Factibles y la
  Solución Optima a los problemas formulados en el
  anterior ejercicio Teórico-Práctico, teniendo
  en cuenta:

• Construcción del Modelo

• Elección y Formulación de las
  Variables

• Evaluación y Formulación de las
  Restricciones

• Formulación de la Función
  Objetivo

• Elección del Método a Usar

• Desarrollo del Método y Obtención de
  Resultados

Desarrollo del
trabajo

• a. Cuando los consumidores se encuentran muy
  dispersos, la venta directa resultaría
  impráctica por los costos tan altos de
  transporte.

Unos grandes almacenes desean liquidar 200 camisas y 100
pantalones de la temporada anterior. Para ello lanzan, dos
ofertas, A y B. La oferta A consiste en un lote de una camisa y
un pantalón, que se venden a 30 €; la oferta B
consiste en un lote de tres camisas y un pantalón, que se
vende a 50 €. No se desea ofrecer menos de 20 lotes de la
oferta A ni menos de 10 de la B. ¿Cuántos lotes ha
de vender de cada tipo para maximizar la ganancia?

1.1 Elección y Formulación de las
Variables

X = Nº de Lotes de A

Y = Nº de lotes de B

1.2 Evaluación y Formulación de las
Restricciones

X + 3Y = 200

X + Y = 100

X = 20

Y = 10

1.3 Formulación de la Función
Objetivo

F (X, Y) = 30X + 50Y

1.4 Elección del Método a Usar

Conjunto de soluciones factibles:

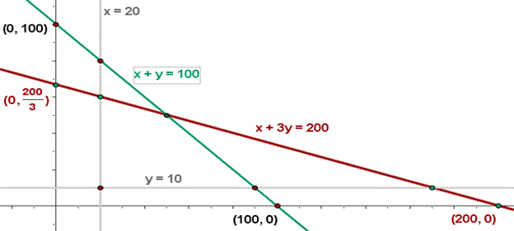
Calculando las coordenadas de los vértices del
recinto de las soluciones factibles.

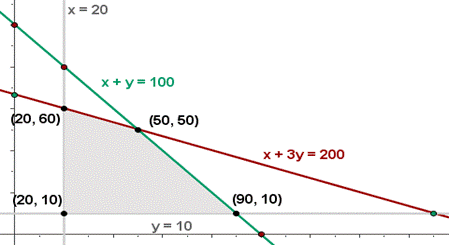
1.5 Desarrollo del Método y Obtención de
Resultados.

Calculando el valor de la función
objetivo:

F (X, Y) = 30X + 50Y

F (X, Y) = 30(20) + 50(10) = 1100 Euros

F (X, Y) = 30(90) + 50(10) = 3200 Euros

F (X, Y) = 30(20) + 50(60) = 3600 Euros

F (X, Y) = 30(50) + 50(50) = 4000 Euros –
Máximo

Con 50 lotes de cada tipo se obtiene una ganancia
máxima de 4000 Euros.

• b. Los productos perecederos requieren canales
  directos o muy cortos.

Una empresa de transportes tiene dos tipos de camiones,
los del tipo A con un espacio refrigerado de 20 m3 y un espacio
no refrigerado de 40 m3. Los del tipo B, con igual cubicaje
total, al 50% de refrigerado y no refrigerado. La contratan para
el transporte de 3 000 m3 de producto que necesita
refrigeración y 4 000 m3 de otro que no la necesita. El
coste por kilómetro de un camión del tipo A es de
30 € y el B de 40 €. ¿Cuántos camiones de
cada tipo ha de utilizar para que el coste total sea
mínimo?

1.1 Elección y Formulación de las
Variables

X = Camiones de tipo A

Y = Camiones de tipo B

1.2 Evaluación y Formulación de las
Restricciones

20X + 30Y = 3000

40X + 30Y = 4000

X = 0

Y = 0

1.3 Formulación de la Función
Objetivo

F (X, Y) = 30X + 40Y

1.4 Elección del Método a Usar

Conjunto de soluciones factibles:

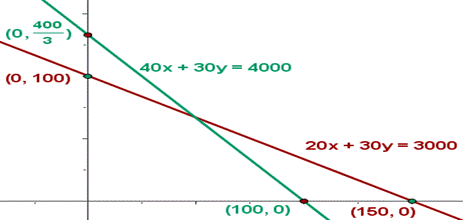
Recinto de las soluciones factibles

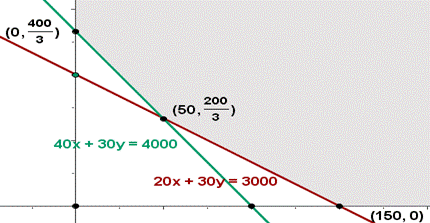
1.5 Desarrollo del Método y Obtención de
Resultados.

Calculando la función objetivo

F (X, Y) = 30X + 40Y

F (0, 400/3) = 30 (0) + 40 (400/3) = 5333.33

F (0, 150/0) = 30 (150) + 40 (0) = 4500

Como X y Y han de ser números naturales
redondeamos el valor de Y.

F (50, 67) = 30 (50) + 40 (67) = 4180
Mínimo

El costo mínimo seria de 4150 Euros para A = 50 y
B = 67

• c. Los requerimientos de los comerciantes y las
  capacidades de los distribuidores.

Unos grandes almacenes encargan a un fabricante
pantalones y chaquetasdeportivas. El fabricante dispone para la
confección de 750 m de tejido de algodón y 1000m de
tejido de poliéster. Cada pantalón precisa 1m de
algodón y 2m de poliéster. El precio del
pantalón se fija en 50 pesos y el de la chaqueta en 40
pesos. ¿Qué numero de pantalones y chaquetas debe
suministrar el fabricante a los almacenes para que estos consigan
una venta máxima?

1.1 Elección y Formulación de las
Variables

X = Nº de pantalones

Y = Nº de chaquetas

1.2 Evaluación y Formulación de las
Restricciones

X + 1.5Y = 750

2X + 37 = 1500

2X + Y = 1000

X = 0

Y = 0

1.3 Formulación de la Función
Objetivo

F(X, Y) = 50X + 40Y

1.4 Elección del Método a Usar

Al ser X = 0 y Y = 0

Solución a los sistemas:

2X + 3Y = 1500; X = 0 (0, 500)

2X + Y = 1000; Y = 0 (500,0)

2X + 3Y = 1500; 2X + Y = 1000 (375, 250)

1.5 Desarrollo del Método y Obtención de
Resultados.

F(X, Y) = 50X + 40Y

F (0, 500) = 50 (0) + 40 (500) = 20000

F (500,0) = 50 (500) + 40 (0) = 25000

F (375, 250) = 50 (375) + 40 (250) = 28750

L solución optima es fabricar 375 pantalones y
250 chaquetas para obtener un beneficio de 28750.

• d. El precio fijado a cada unidad de un
  producto influye en la cantidad de fondos disponibles para su
  distribución.

Considere que una fábrica puede elaborar hasta
150 unidades en cada uno de los 4 periodos en que se ha
subdividido el horizonte de planificación y se tiene
adicionalmente la siguiente información:

Adicionalmente considere que se dispone de un Inventario
Inicial de 15 unidades y no se acepta demanda pendiente o
faltante, es decir, se debe satisfacer toda la demanda del
período.

1.1 Elección y Formulación de las
Variables

X = Unidades elaboradas en el periodo t (con t= 1, 2, 3,
4)

Y = Unidades en inventario al final del periodo t (con
t= 1, 2, 3, 4)

1.2 Evaluación y Formulación de las
Restricciones

• Capacidad de Producción por Período:
  Xt <= 150 (Con t =1,2,3,4)

• Satisfacer Demanda Período 1: X1 + Y0 – Y1
  = 130 (Y0 = 15)

• Satisfacer Demanda Período 2: X2 + Y1 – Y2
  = 80

• Satisfacer Demanda Período 3: X3 + Y2 – Y3
  = 125

• Satisfacer Demanda Período 4: X4 + Y3 – Y4
  = 195

• No Negatividad: Xt >=0, Yt
  >=0

1.3 Formulación de la Función
Objetivo

Minimizar 6X1 + 4X2 + 8X3 + 9X4 + 2Y1 + 1Y2 + 2.5Y3 +
3Y4

1.4 Elección del Método a Usar

X1=115, X2=150, X3=100, X4=150, Y1=0, Y2=70, Y3=45,
Y4=0.

1.5 Desarrollo del método y obtención de
resultados

6X1 + 4X2 + 8X3 + 9X4 + 2Y1 + 1Y2 + 2.5Y3 +
3Y4

6 (115) + 4 (150) + 8 (100) + 9 (150) + 2 (0) + 1 (70) +
2.5 (45) + 3 (0)

690 + 600 + 800 + 1350 + 0 + 70 + 112.5 + 0

Valor Óptimo V (P)=3.622,5

• e. Cuando el tamaño de los pedidos o el
  volumen total del negocio es mínimo, la
  distribución indirecta resultaría
  costosa.

Una empresa tiene dos factorías A y B. En ellas
se fabrica un determinado producto, a razón de 500 y 400
unidades por día respectivamente. El producto ha de ser
distribuido posteriormente a tres centros I, II y III, que
requieren, respectivamente, 200, 300 y 400 unidades. Los costos
de transportar cada unidad del producto desde cada
factoría a cada centro distribuidor son los indicados en
la tabla siguiente:

¿De qué manera deben organizar el
transporte a fin de que los gastos sean
mínimos?

1.1 Elección y Formulación de las
Variables

X ¡j Cantidad de producto a enviar desde la
factoría i (i = A, B) hasta el centro j (j = 1, 2,
3)

1.2 Evaluación y Formulación de las
Restricciones

• XA1 + XA2 + XA3 = 500

• XB1 + XB2 + XB3 = 400

• XA1 + XB1 = 200

• XA2 + XB2 = 300

• XA3 + XB3 = 400

• X0 = 0

1.3 Formulación de la Función
Objetivo

50 XA1 + 60XA2 + 10XA3 + 25XB1 + 40XB2 +
20XB3

1.4 Elección del Método a Usar

1.5 Desarrollo del método y obtención de
resultados

Conclusiones

Se puede concluir que estos modelos
determinísticos estudiados anteriormente conllevan a la
aplicación de distintos modelos principalmente
relacionados con la distribución eficaz de recursos
limitados que, apoyados con sistemas (solucionando problemas en
grupo) reflejan un concepto eficiente y definido para cada
situación dada, a fin de resolver el modelo.

Para la solución de un determinado problema, se
debe identificar primero un criterio mediante el cual se escoge
un modelo a seguir cuyos parámetros fluctúen de
manera efectiva; esto establece el rendimiento o efectividad que
resulte en términos de menos costos y más
beneficios, ya que el enfoque de solución de problemas es
para ayudar en la toma de decisiones. En estos modelos
determinísticos como la función objetivo (la cual
define la cantidad que se va a maximizar o minimizar), las
variables (las entradas controlables en el sistema) y las
restricciones (limitan o reducen el grado en que se persigue el
objetivo) se centra la obtención del liderazgo empresarial
en el desarrollo de estrategias que conlleve a una ventaja
competitiva.

Bibliografía

• http://www.monografias.com/trabajos-pdf4/ejercicios-resueltos-programacion-lineal-2da-parte/ejercicios-resueltos-programacion-lineal-2da-parte.pdf.
  Ejercicios resueltos de programación lineal Ing.
  José Luis Albornoz Salazar, Septiembre de
  2010.

• http://www.contrib.andrew.cmu.edu/~mgoic/files/documents/optimization/modelos.pdf
  Modelamiento de problemas de Programación Lineal con
  Variables Continuas, Universidad de Chile, Facultad de
  Ciencias Físicas y Matemáticas, Departamento de
  Ingeniería Industrial.

• http://es.wikipedia.org/wiki/Modelo_determin%C3%ADstico,
  Modelos Determinísticos, Licencia Creative Commons
  Atribución Compartir Igual 3.0 mayo de
  2012.

• http://www.deltaasesores.com/articulos/gestion-de-proyectos/349-administracion-de-proyectos-i-.
  Administración de Proyectos I.

• http://metodoscuantitativo2.galeon.com/.
  Introducción a la Programación
  Lineal.

Autor:

Inocencio Meléndez Julio.

Magíster en Administración

Magíster en Derecho

Doctorando en Derecho Patrimonial: La
Contratación Contemporánea.