La Trigonometría

Introducción

La Trigonometría, palabra que significa
"medición" de triángulos, en la que la palabra
deriva de "tri" que significa "tres", el "gono" que significa
"ángulo" y por ultimo "metria" que es "medición es
parte fundamental de la Matemática que estudia los
ángulos y lados de los triángulos, con ella se es
posible calcular o medir distancias indirectamente, como por
ejemplo, la distancia que separa la Tierra de la Luna.

Ya desde tiempos de la antigüedad, los Egipcios
establecieron la medida de los ángulos en grados, minutos
y segundos; pero aun así, la trigonometría no
empezó a haber hasta la Grecia clásica, donde la
escuela de Pitágoras desarrollo el Teorema que lleva su
nombre, en la que expone que "En todo triángulo
rectángulo el cuadrado de la Hipotenusa es igual a la suma
de los cuadrados de los catetos".

El conocimiento de esta Ciencia Matemática nos ha
dejado grandes monumentos de la antigüedad, en aquellos
países donde se estudiaba la trigonometría,
plasmando en ellas la precisión matemática aun
más que la artística.

Pero la Trigonometría es extensa y complicada, y
su vez es indispensable en demás ramas científicas,
como la Física, la Arquitectura e ingeniera; y es por ello
que desarrolle y presento LA INNOVACION EN EL MUNDO
TRIGONOMÉTRICO, donde la idea fundamental, es la de
facilitar el estudio y la aplicación de la
Trigonometría, de una forma diferente a la presenta y
estudiada por muchos años.

El teorema que presentare se basa principalmente en el
conocimiento del Perímetro de una circunferencia.
Además dejare en claro que la Matemática no es una
ciencia limitada, sino más bien que la Ciencia es una
Matemática y que en ella se encierra todo el conocimiento
que creo al Universo, visto por el horizonte de la Lógica
Matemática.

Trigonometría

Para empezar definiré lo que es un
Triángulo, el Angulo y lo que es el
Perímetro.

El Triángulo es un polígono que posee tres
lados, y según la longitud de esos lados, el
triángulo se clasificara en tres formas, la primera
Equiláteros, cuando poseen sus tres lados iguales, el
Isósceles, si poseen dos lados iguales y por ultimo
Escaleno, si todos sus lados son diferentes. La suma de los tres
ángulos de un Triángulo es de 180°
independientemente de la longitud de sus lados.

No olvidemos que el Triángulo recto cumple con
una relación métrica entre sus lados, la cual es el
teorema de Pitágoras, en la que reza que la Hipotenusa
será igual a la suma de los cuadrados de los
catetos.

Por las longitudes de sus lados, todo triángulo
se clasifica:

• TRIANGULO EQUILATERO: si todos sus lados
  tienen la misma longitud (los tres ángulos internos
  miden 60 grados ó radianes.)

• TRIANGULO ISOSCELES: (del griego
  iso, igual, y skelos, piernas; es decir,
  "con dos piernas iguales"), si tiene dos lados de la misma
  longitud. Los ángulos que se oponen a estos lados
  tienen la misma medida.

• TRIANGULO ESCALENO: ("cojo", en griego), si
  todos sus lados tienen longitudes diferentes (en un
  triángulo escaleno no hay dos ángulos que
  tengan la misma medida).

La Circunferencia se define como una curva cerrada y
plana, cuyos puntos equidistantes de otro interior llamado
centro; y el Perímetro como la longitud de sus
lados.

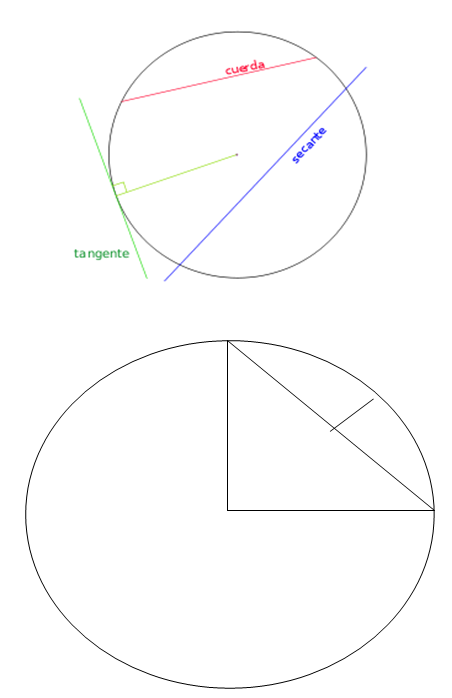
Si trazamos dos (2) segmentos a una semicircunferencia
(90°), los cuales serán denominados AB y CD, donde el
segmento AB es el que une los puntos extremos del radio a
90°, y si a esta se le traza otro segmento CD, el cual se
sitúa a la mitad de la semicircunferencia y el segmento
AB; obtenemos que sumando ambos segmentos AB +CD/2, obtenemos el
perímetro de la semicircunferencia; es decir, de radio
igual a 1, con el ángulo alfa 90°, el segmento AB es
igual a 1,4 y el segmento CD 0,34/2, lo que es 0,17.

P=AB+CD/2

=1,4+0,34/2

=1,57.

Todo esto nos lleva a definir un enunciado, el cual
es:

EL PERIMETRO DE UNA SEMICIRCUNFERENCIA VENDRA DADA POR
LA SUMA DE LOS SEGMENTOS AB Y CD/2.

P=AB + CD/2.

De lo anteriormente expuesto, se deduce la siguiente
expresión matemática:

P=R x Sen alfa x 1,57.

Donde P es igual al perímetro

R es igual a radio.

Seno de alfa igual a 90°.

1,57 es la suma de AB+CD/2

Para demostrar ello citaré un
ejemplo, donde calculare el perímetro de una
circunferencia a partir de la ecuación anteriormente
expuesta (P=R x Sen Alfa x 1,57.) Y la ecuación que ya
todos conocemos (P=2 x Pi x R).

Ejemplo: Se tiene una circunferencia de Radio igual a 2
cms, calcular su perímetro.

Según la ecuación de P=2 x Pi x
R;

=2 x 3,14 x 2 cms.

=12,56 cms.

Ahora según la ecuación de P=R x Sen Alfa
X 1,57.

= 2 cms. x Sen 90° x 1,57

= 3, 14 cms.

Pero ahora bien, según esta ecuación el
perímetro de la circunferencia es igual o para los
90°, por lo que solo es una parte del perímetro real,
es decir, de los 360° ; y para ello, se procederá a
realizar una simple regla de tres (3).

3,14cms.————- 90°

12,56cms.————360°

NOTA: Si se necesita obtener o conocer el
perímetro de una semicircunferencia X, en la cual el valor
del Seno de Alfa es mayor o menor a los 90°; se deberá
realizar una regla de tres (3) para hallar o conocer el valor
real de dicho perímetro; ya que el perímetro que se
obtenga con la ecuación P=R x Sen Alfa. (90°) x 1,57.
Es con respecto a los 90° grados.

Perímetro y
trigonometría

El teorema de Pitágoras dice que en un triangulo
rectángulo el cuadrado de la longitud de la hipotenusa es
igual a la suma de los cuadrados de las longitudes de los
catetos; por lo que se representa de la siguiente forma: los
catetos tienen longitudes a y b, y la medida de la hipotenusa es
c, se establece lo siguiente:

Ahora bien, si se es posible calcular el
perímetro de una circunferencia con el enunciado
anteriormente expuesto, se puede también resolver
problemas trigonométricos; veamos como hacerlo:

Si tenemos un triángulo cualquiera, y de una u
otra forma conocemos la hipotenusa de dicho triángulo,
podemos ver que se puede dibujar una semicircunferencia, lo que
quiere decir que es posible obtener o conocer los demás
lados restantes del triángulo.

Ejemplo: Si se tiene un triángulo del cual solo
se conoce su hipotenusa, la cual es de 5,6cms su ángulo
(Sen alfa) es de 45°; y además sus otros dos catetos
restantes son iguales entre sí. Calcule los dos
catetos.

Procedemos primero a calcular el
perímetro.

P= 5,6cms x Sen 90° x 1,57.

= 8,79cms.

Una vez obtenido el perímetro, procedemos a
calcular el valor de los segmentos AB y CD.

Para hallar los valores de los segmentos antes
mencionados procedemos de la siguiente forma:

P=AB + CD/2 es decir, P=1,4 + 0,34/2=1,57.

Se procede ahora a un simple despeje,
así:

AB=Px/1,57×1,4.

CD=Px/1,57×0,34/2.

8,79cms/1,57=5,59cms.x 1,4=
7,83cms.

8,79cms/1,57=5,59cms.x
0,34/2=0,95cms.

Una vez conocidos los valores de los segmentos y del
perímetro, se procederán a calcular los dos
catetos.

El cateto adyacente vendrá dado por la resta de
la Hipotenusa o del radio y del valor del segmento CDx2,
así:

C.A.=Hipotenusa o radio –
CDx2=

= 5,6cms.- 0,95cmsx2-

=3,7cms.

Teniendo en cuenta que ambos catetos son iguales entre
sí, se deduce que el cateto opuesto es también de
3,7 cms.

Un paso
más

Como lo he demostrado, conociendo el valor de la
hipotenusa y el valor del ángulo Alfa, la
resolución del problema es simple; solo hay que calcular
el perímetro de dicha semicircunferencia, luego calcular
los valores de los segmentos AB y CD para así entonces
hallar el valor de los catetos adyacente y opuesto.

Pero ahora bien, que tal si no conocemos el valor de la
hipotenusa, sino el valor de cualquier cateto, pero conociendo el
valor del ángulo Alfa.

Para resolver este problema, se procederá a
realizar una operación sencilla de "conversión o
una escala"; es decir, el valor del cateto X conocido lo
tomaremos como el valor de la hipotenusa. De esta manera se
procederá a resolver el problema sin ninguna
dificultad.

Pero una vez resuelto el problema, se procederá a
dividir el valor del cateto X obtenido en la operación por
la del cateto X conocido anteriormente, el valor o producto de
dicha operación se lo multiplicara por el valor del cateto
restante y de la hipotenusa, obtenida inicialmente en la
operación, de esta forma, se obtiene el valor real de
todos los lados del triángulo.

Para ello citare un ejemplo: Si se tiene un
triángulo cualquiera, de cual se conoce su cateto
adyacente, el cual mide 4 cms. Y el ángulo Alfa es de
40°. Calcule el cateto opuesto y la hipotenusa.

DATOS:

H=?

C.A.=4cms.

C.O.=?

P=?

AB=?

CD=?

Alfa=40°

Para empezar, tomaremos al valor C.A. como
Hipotenusa.

C.A.=H.

Ahora procedemos a calcular el perímetro de la
circunferencia.

P=RxSen Alfa 1,57.

P=4cms x Sen 90° x 1,57.

P=6,28 cms.

Enseguida procedemos a la regla de tres (3) para hallar
el valor real del perímetro en este caso de
80°.

90°———6,28cms.

80°———5,58cms.

Entonces el valor real del perímetro en este caso
es de 5,58cms.

El siguiente paso, es de hallar los valores de los
segmentos AB y CD., lo que para ello procederemos de la siguiente
forma:

P=AB + CD/2

5,58 cms.= 1,4 + 0,34/2=1,57

AB=5,58/1,4 x 1,57=6,25.

CD=5,58/1,57 x 0,34/2=0,60.

C.A.=H o R-( CD x2)=

=4 cms. – 1,20cms.
=2,8cms.

C.O.=AB/2

=4,9 cms./2 = 2,45 cms.

Ahora bien, hecho ya todo esto, se procederá a
realizar las "conversiones":

Se tiene que C.A.=4cms
inicialmente.

El valor de C.A. final es de
2,8cms.

El siguiente paso será el de dividir el C.A.
inicial sobre el C.A. final:

C.A.i/C.A.f=4cms/2,8cms.

=1,428cms.

El valor 1,428 será el factor
multiplicador, así:

H=4cms. 4cms. x 1,428=5,68
cms.

C.O.=2,45cms. 2,45 cms. x
1,428cms.=3,47cms

C.A.=2,8 cms. 2,8cms. x
1,428cms.=3,97cms.

NOTA: Si le restamos el valor de la hipotenusa o el
radio al valor del segmento CD, se puede obtener el valor del
C.A.; pero el valor del CD, debe ser multiplicado por el factor
2, ya que el valor CD/2 nos da la suma, junto con el segmento AB,
del perímetro, pero el valor real de la distancia entre el
segmento AB y el punto de la circunferencia, es el doble del
valor usado para calcular el perímetro.

TRIGONOMETRIA

Circunferencia

Se define una circunferencia como una curva cerrada y
plana, cuyos puntos equidistantes de otro interior llamado
centro; y el perímetro como la longitud de sus
lados.

Si trazamos dos (2) segmentos a una semicircunferencia
(90°), los cuales serán denominados AB y CD, donde el
segmento AB es el que une los puntos extremos del radio a
90°, y si a esta se le traza otro segmento CD, el cual se
sitúa a la mitad de la semicircunferencia y el segmento
AB; obtenemos que sumando ambos segmentos AB +CD/2, obtenemos el
perímetro de la semicircunferencia; es decir, de radio
igual a 1, con el ángulo alfa 90°, el segmento AB es
igual a 1,4 y el segmento CD 0,34/2, lo que es 0,17.

P=AB+CD/2

=1,4+0,34/2

=1,57.

Todo esto nos lleva a definir un enunciado, el cual
es:

EL PERIMETRO DE UNA SEMICIRCUNFERENCIA VENDRA DADA POR
LA SUMA DE LOS SEGMENTOS AB Y CD/2.

P=AB + CD/2.

De lo anteriormente expuesto, se deduce la siguiente
expresión matemática:

P=R x Sen alfa x 1,57.

Donde P es igual al
perímetro

R es igual a radio.

Seno de alfa igual a 90°.

1,57 es la suma de AB+CD/2

.

NOTA: Si se necesita obtener o conocer el
perímetro de una semicircunferencia X, en la cual el valor
del Seno de Alfa es mayor o menor a los 90°; se deberá
realizar una regla de tres (3) para hallar o conocer el valor
real de dicho perímetro; ya que el perímetro que se
obtenga con la ecuación P=R x Sen Alfa. (90°) x 1,57.
Es con respecto a los 90° grados.

Ahora bien, si se es posible calcular el
perímetro de una circunferencia con el enunciado
anteriormente expuesto, se puede también resolver
problemas trigonométricos; veamos como hacerlo:

Si tenemos un triángulo cualquiera, y de una u
otra forma conocemos la hipotenusa de dicho triángulo,
podemos ver que se puede dibujar una semicircunferencia, lo que
quiere decir que es posible obtener o conocer los demás
lados restantes del triángulo.

Ejemplo: Si se tiene un triángulo del cual solo
se conoce su hipotenusa, la cual es de 5,6cms su ángulo
(Sen alfa) es de 45°; y además sus otros dos catetos
restantes son iguales entre sí. Calcule los dos
catetos.

Procedemos primero a calcular el
perímetro.

P= 5,6cms x Sen 90° x 1,57.

= 8,79cms.

Una vez obtenido el perímetro, procedemos a
calcular el valor de los segmentos AB y CD.

Para hallar los valores de los segmentos antes
mencionados procedemos de la siguiente forma:

P=AB + CD/2 es decir, P=1,4 +
0,34/2=1,57.

Se procede ahora a un simple despeje,
así:

AB=Px/1,57×1,4.

CD=Px/1,57×0,34/2.

8,79cms/1,57=5,59cms.x 1,4=
7,83cms.

8,79cms/1,57=5,59cms.x
0,34/2=0,95cms.

Una vez conocidos los valores de los segmentos y del
perímetro, se procederán a calcular los dos
catetos.

El cateto adyacente vendrá dado por la resta de
la Hipotenusa o del radio y del valor del segmento CDx2,
así:

C.A.=Hipotenusa o radio –
CDx2=

= 5,6cms.- 0,95cmsx2 =3,7cms.

Teniendo en cuenta que ambos catetos son iguales entre
sí, se deduce que el cateto opuesto es también de
3,7 cms.

UN PASO MÁS

Como lo he demostrado, conociendo el valor de la
hipotenusa y el valor del ángulo Alfa, la
resolución del problema es simple; solo hay que calcular
el perímetro de dicha semicircunferencia, luego calcular
los valores de los segmentos AB y CD para así entonces
hallar el valor de los catetos adyacente y opuesto.

Pero ahora bien, que tal si no conocemos el valor de la
hipotenusa, sino el valor de cualquier cateto, pero conociendo el
valor del ángulo Alfa.

Para resolver este problema, se procederá a
realizar una operación sencilla de "conversión o
una escala"; es decir, el valor del cateto X conocido lo
tomaremos como el valor de la hipotenusa. De esta manera se
procederá a resolver el problema sin ninguna
dificultad.

Pero una vez resuelto el problema, se procederá a
dividir el valor del cateto X obtenido en la operación por
la del cateto X conocido anteriormente, el valor o producto de
dicha operación se lo multiplicara por el valor del cateto
restante y de la hipotenusa, obtenida inicialmente en la
operación, de esta forma, se obtiene el valor real de
todos los lados del triángulo.

Para ello citare un ejemplo: Si se tiene un
triángulo cualquiera, de cual se conoce su cateto
adyacente, el cual mide 4 cms. Y el ángulo Alfa es de
40°. Calcule el cateto opuesto y la hipotenusa.

DATOS:

H=?

C.A.=4cms.

C.O.=?

P=?

AB=?

CD=?

Valor C.A.

Alfa=40°

Para empezar, tomaremos al C.A.=H. como
Hipotenusa.

Ahora procedemos a calcular el perímetro de la
circunferencia.

P=RxSen Alfa 1,57.

P=4cms x Sen 90° x 1,57.

P=6,28 cms.

Enseguida procedemos a la regla de tres (3) para hallar
el valor real del perímetro en este caso de
80°.

90°———6,28cms.

80°———5,58cms.

Entonces el valor real del perímetro en este caso
es de 5,58cms.

El siguiente paso, es de hallar los
valores de los segmentos AB y CD., lo que para ello procederemos
de la siguiente forma:

P=AB + CD/2

5,58 cms.= 1,4 + 0,34/2=1,57

AB=5,58/1,57 x 1,4=4,9.

CD=5,58/1,57 x 0,34/2=0,60.

C.A.=H o R-( CD x2)=

=4 cms. – 1,20cms.

=2,8cms.

C.O.=AB/2

=4,9 cms./2

= 2,45 cms.

Ahora bien, hecho ya todo esto, se procederá a
realizar las "conversiones":

Se tiene que C.A.=4cms
inicialmente.

El valor de C.A. final es de
2,8cms.

El siguiente paso será el de
dividir el C.A. inicial sobre el C.A. final:

C.A.i/C.A.f=4cms/2,8cms.

=1,428cms.

El valor 1,428 será el factor multiplicador,
así:

H=4cms. 4cms. x 1,428=5,68
cms.

C.O.=2,45cms. 2,45 cms. x
1,428cms.=3,47cms

C.A.=2,8 cms. 2,8cms. x
1,428cms.=3,97cms.

NOTA: Si le restamos el valor de la hipotenusa o el
radio al valor del segmento CD, se puede obtener el valor del
C.A.; pero el valor del CD, debe ser multiplicado por el factor
2, ya que el valor CD/2 nos da la suma, junto con el segmento AB,
del perímetro, pero el valor real de la distancia entre el
segmento AB y el punto de la circunferencia, es el doble del
valor usado para calcular el perímetro.

CUANDO EL ÁNGULO Q ES MAYOR QUE
90°

Para resolver un determinado problema
trigonométrico, donde el valor del ángulo Q es
mayor que los 90° y se lo desconoce, se necesitara saber
entonces el ángulo Alfa y el ángulo Y, dos lados,
la Hipotenusa y un cateto cualquiera.

Citaremos un ejemplo donde se tiene un triángulo,
cuya Hipotenusa se conoce junto con el cateto opuesto, y el
ángulo Alfa es X, calcularemos entonces el cateto
Adyacente.

1) Lo primero será calcular el Perímetro
que describe el triángulo.

2) Luego calculamos es seg. AB.; el resultado lo
dividiremos sobre 2.

3) Se tiene que el seg. AB, será igual al C.O.,
del "segundo triángulo", entonces el cateto del "primer
triángulo" será ahora la Hipotenusa.

4) Por el Teorema de Pitágoras, podemos conocer
el valor del C.A. del segundo triángulo; también se
puede proceder a calcularlo por el método del
Perímetro, pero seria un poco más
extenso.

5) Teniendo todo esto, se procede ahora a calcular el
C.A. del primer triángulo, sumando el valor del C.A. del
segundo triángulo mas el valor del CD del primer
triángulo(Multiplicado por 2), y luego se lo restamos a la
Hipotenusa del primer triángulo.

De esta forma, se puede calcular o conocer el lado
deseado, a partir de los otros lados, además de conocer el
ángulo Alfa y que el ángulo Q no sea mayor que
90°.

Problemas
trigonométricos

CONTINUACIÓN, BRINDARE UN ESQUEMA A SEGUIR PARA
RESOLVER PROBLEMAS TRIGONOMÉTRICOS.

Para hallar el cateto opuesto y el adyacente conociendo
la Hipotenusa, el ángulo Alfa y el ángulo Q igual a
90; procedemos así:

Procedemos a calcular El Perímetro.

P=R x Sen Alfa 90° x 1,57.

Ángulo mayor o menor que
90°

Si No.

Procede a la regla de Tres, para conocer el valor real
Del Perímetro de la semicircunferencia Descrita por el
triángulo.

Calculamos el valor del segmento
AB.

AB=P/1,57 x 1,4.

El valor del segmento AB lo dividimos Sobre dos (2),
ello será igual a El cateto opuesto.

Calculamos el segmento CD.

CD=P/1,57 x 0,17.

Para hallar el Cateto Adyacente, multiplicamos el seg.
CD x 2, luego restamos la H. Al seg. CD. , Así:C.A=H-(CD x
2).

ESTE ESQUEMA NOS SERVIRA PARA DESCRIBIR LOS PASOS A
SEGUIR SI DESEAMOS CALCULAR EL PERÍMETRO DE CUALQUIER
CIRCUNFERENCIA.

Multiplicamos el Radio o la Hipotenusa Por
el Sen 90° y todo ello por el valor de 1,57.

P=R x Sen Alfa 90° x 1,57.

El valor calculado es con respecto A los 90°, para
hallar el Perímetro de la Circunferencia de un
ángulo mayor o menor A los 90°, procedemos a la regla
de tres.

Si deseamos también calcular El segmento AB,
procedemos así: Dividimos el Perímetro sobre 1,57
luego lo multiplicamos por 1,4

AB=P/1,57 x 1,4.

Si también deseamos calcular El segmento CD,
procedemos de la Siguiente forma: Dividimos el Perímetro
sobre 1,57, luego lo multiplicamos por 1,4.

CD=P/1,57 x 0,17.

PARA HALLAR LA HIPOTENUSA Y EL CATETO CUALQUIERA,
CONOCIENDO SOLO UN CATETO Y EL ÁNGULO ALFA.

Tomaremos el valor del cateto Conocido y lo
consideraremos como La Hipotenusa.

Procedemos a calcular el Perímetro

P=R x Sen Alfa 90° x 1,57.

Ángulo mayor o menor que
90°

Si No

Procedemos a la regla De tres para conocer El valor real
del Perímetro.

Calculamos el valor del segmento AB.

AB=P/1,57 x 1,4.

Calculamos el segmento CD.

CD=P/1,57 x 0,17.

Para hallar el C.A. multiplicamos seg. CD x 2, Luego
restaremos la H.al seg. CD.

C.A.=H.-(CD x 2).

Una vez realizado todo lo anterior, procedemos a
realizar una conversión, lo cual ya a sido explicada
anteriormente.

Perímetro y
demás

Si repasamos acerca de la ecuación de P=AB+CD/2,
podemos hacer una deducción interesante, y es que si se
nos presenta un determinado caso, adonde solo se conozca
cualquier segmento (AB y/o CD) además del ángulo,
se es posible conocer el valor de las demás interrogantes,
veamos como:

Según el enunciado, el perímetro de una
semicircunferencia (90°) vendrá dado por la suma de
los segmentos AB y CD/2, lo que nos permite con un simple
despeje, resolver las demás interrogantes, veamos
como:

Se tiene una semicircunferencia de 90°, lo cual solo
se conoce su segmento CD, el cual es de 0,50cms, calcularemos las
demás interrogantes, siendo estas AB, R y P.

Ahora,

P=4,11cms.+ 0,50cms.

=4,61cms.

Y se tiene que,

P=R x Sen Alfa x 1,57-

R=P/Sen Alfa x 1,57.

=4,61cma/Sen 90° x 1,57.

=2,93cms.

Si queremos estar seguros de ello, o comprobarlo,
podemos hacerlo con la ayuda de la ecuación P=2 x Pi x R.,
a sí se tiene que:

P=2 x 3,14 x 2,93cms.

=18,40 cms.

Pero no olvidemos que esta ecuación nos da el
Perímetro de una circunferencia de 360°, por lo que a
este resultado, se le debe aplicar la regla de tres, para
así conocer el perímetro de 90° de dicha
circunferencia.

Entonces se tiene que:

18,40cms————360°

4,60cms———— 90°

Realizado todo esto, se concluye que conociendo el valor
de cualquier segmento, ya sea AB o CD, además del
ángulo 90° de la semicircunferencia, se es posible
hallar el valor de las demás interrogantes.

PERÍMETRO Y EL VALOR DE
PI

El valor del Pi, desde tiempos antiguo, es conocido; un
matemático holandés Adrián Anthonisz
(1527-1607), tomo el valor de 355/113 para el valor del Pi, el
cual fue empleado durante los siglos XVI y XVII.

El alemán Johana Heinrich Lambert, (1728-1777)
obtuvo el valor de una fracción ordinaria la que el
numerador tenia dieciséis cifras y el denominador
quince.

Pero continuación demostrare el valor de Pi,
según a todo lo anteriormente planteado.

Si entendemos bien, que si tenemos una
semicircunferencia de 90°, donde el radio es igual a 1, y a
esta se le traza dos segmentos, los que serán AB y CD,
ello nos dará el valor de 1,57. y es curioso que ello sea
igual al valor de Pi dividido por dos, así:
Pi/2=1,57.

Si tenemos una circunferencia de radio igual a 1, y
entendemos que el Perímetro de ella será igual a
6,28, y procedemos a dividir la circunferencia en dos partes
iguales, ello nos dará el valor igual al del Pi 3,14., Es
decir, Pi es igual a P/2 pero también es P=(AB+CD/2) x
2.

RESOVER PROBLEMAS TRIGONOMÉTRICOS, A TRAVES DEL
TEOREMA DE PITAGORAS, PERO CON EL ÁNGULO Q MAYOR QUE
90°.

El Teorema de Pitágoras nos es útil para
resolver problemas Trigonométricos, pero su uso es
limitado, ya que se requiere que el Ángulo Q sea igual a
los 90°. Pero si "fusionamos" el teorema de Pitágoras
junto con el enunciado del "Perímetro", entonces si
será posible resolver problemas Trigonométricos,
donde el Ángulo Q es mayor que 90°.

Para ello, citaré un ejemplo: Si tenemos un
triángulo donde se conoce el Cateto Adyacente y el Opuesto
y además conocemos el valor del ángulo Q,
procederíamos así:

• 1) Primero calcularemos el ángulo Y, de
  la siguiente forma:

• 2) Restaremos 180° al ángulo
  Q.

• 3) El valor obtenido de dicha operación,
  se la sumaremos al valor del Ángulo Q2, para luego
  restarlo a los 180°, y el producto será el valor
  del ángulo Y1.

• 4) Conocido ya el Ángulo Y1, procedemos
  a calcular el Perímetro de la semicircunferencia que
  describe el "segundo Triángulo".

• 5) Conocido el Perímetro, calculamos el
  segmento AB y CD.

• 6) El segmento AB lo dividimos en 2, el cual lo
  sumaremos al Cateto Adyacente del "primer triángulo",
  lo cual será el Cateto Adyacente final.

• 7) Restaremos el C.O. del "primer
  triángulo" al valor del segmento CD (este segmento
  multiplicado por 2), así entonces obtenemos el Cateto
  Opuesto final.

• 8) Por ultimo, procedemos a calcular la
  Hipotenusa según el teorema de
  Pitágoras.

Siguiendo todos estos pasos descritos anteriormente,
él calculo de la Hipotenusa en un triángulo donde
el Ángulo Q es mayor que los 90°, es
posible.

Para resolver un problema similar, donde solo se conozca
un lado y se desea calcular los otros dos lados restantes, se
necesitara conocer los ángulos Alfa, Q y Y.

• 1) Lo primero es calcular el Perímetro
  descrito por el triángulo.

• 2) Calculamos el seg. AB, luego lo dividimos
  sobre 2, el resultado será el C.O. del "segundo
  triángulo".

• 3) Ahora procedemos a calcular el ángulo
  Y1, así:

Restamos 180° al ángulo Q, el resultado lo
sumamos a los 90°, luego el producto lo restamos a los
180° nuevamente, el resultado final, será el
ángulo Y.

• 4) Procedemos a calcular el Perímetro
  descrito por el "segundo triángulo" realizando una
  "conversión", es decir, usaremos el valor del seg. AB,
  como la Hipotenusa del "segundo triángulo"

• 5) Una vez hecho todo esto, el C.A. será
  hallado sumando el C.A. de "segundo triángulo" mas el
  doble del valor del seg. CD del "primer triángulo"; el
  producto restará a la Hipotenusa del primer
  triángulo.

• 6) El C.O. es igual a la Hipotenusa del
  "segundo triángulo".

RESOVER PROBLEMAS TRIGONOMÉTRICOS, A TRAVES DEL
TEOREMA DE PITAGORAS, PERO CON EL ÁNGULO Q MAYOR QUE
90°

El Teorema de Pitágoras nos es útil para
resolver problemas Trigonométricos, pero su uso es
limitado, ya que se requiere que el Ángulo Q sea igual a
los 90°. Pero si "fusionamos" el teorema de Pitágoras
junto con el enunciado del "Perímetro", entonces si
será posible resolver problemas Trigonométricos,
donde el Ángulo Q es mayor que 90°.

Para ello, citaré un ejemplo: Si tenemos un
triángulo donde se conoce el Cateto Adyacente y el Opuesto
y además conocemos el valor del ángulo Q,
procederíamos así:

• 1) Primero calcularemos el ángulo Y, de
  la siguiente forma:

• 2) Restaremos 180° al ángulo
  Q.

• 3) El valor obtenido de dicha operación,
  se la sumaremos al valor del Ángulo Q2, para luego
  restarlo a los 180°, y el producto será el valor
  del ángulo Y1.

• 4) Conocido ya el Ángulo Y1, procedemos
  a calcular el Perímetro de la semicircunferencia que
  describe el "segundo Triángulo".

• 5) Conocido el Perímetro, calculamos el
  segmento AB y CD.

• 6) El segmento AB lo dividimos en 2, el cual lo
  sumaremos al Cateto Adyacente del "primer triángulo",
  lo cual será el Cateto Adyacente final.

• 7) Restaremos el C.O. del "primer
  triángulo"al valor del segmento CD (este segmento
  multiplicado por 2), así entonces obtenemos el Cateto
  Opuesto final.

• 8) Por ultimo, procedemos a calcular la
  Hipotenusa según el teorema de Pitagoras.

Siguiendo todos estos pasos descritos anteriormente,
él calculo de la Hipotenusa en un triángulo donde
el Ángulo Q es mayor que los 90°, es
posible.

Para resolver un problema similar, donde solo se conozca
un lado y se desea calcular los otros dos lados restantes, se
necesitara conocer los ángulos Alfa, Q y Y.

• 1) Lo primero es calcular el Perímetro
  descrito por el triángulo.

• 2) Calculamos el seg. AB, luego lo dividimos
  sobre 2, el resultado será el C.O. del "segundo
  triángulo".

• 3) Ahora procedemos a calcular el ángulo
  Y1, así:

Restamos 180° al ángulo Q, el resultado lo
sumamos a los 90°, luego el producto lo restamos a los
180° nuevamente, el resultado final, será el
ángulo Y.

• 4) Procedemos a calcular el Perímetro
  descrito por el "segundo triángulo" realizando una
  "conversión", es decir, usaremos el valor del seg. AB,
  como la Hipotenusa del "segundo triángulo"

• 5) Una vez hecho todo esto, el C.A. será
  hallado sumando el C.A. de "segundo triángulo" mas el
  doble del valor del seg. CD del "primer triángulo"; el
  producto restará a la Hipotenusa del primer
  triángulo.

• 6) El C.O. es igual a la Hipotenusa del
  "segundo triángulo".

DEDICATORIA:

Quisiera dedicar este libro en honor y
memoria de todos los Físicos y Matemáticos que han
contribuido al desarrollo de estas Ciencias, la cual a expandido
el saber humano en muchas áreas; Hombres que pesen a las
realidades de su época, lograron desarrollar la
Ciencia.

También quiero dedicarlo muy en
especial a aquellas personas que me han apoyado y estimulado para
la realización de este trabajo, lo que sin ello,
difícilmente hubiera podido lograr.

EL AUTOR.

Autor:

Arturo Correia