Algoritmo
1.- Es una secuencia de pasos o procesos
lógicamente relacionados entre sí a fin de obtener
la solución a un problema planteado.
2.- Es una lista de instrucciones para efectuar paso a
paso un proceso.
3.- Conjunto "FINITO" de pasos o instrucciones, seguidas
en un orden lógico, los cuales nos llevan a la
solución de un problema específico.
4.- Una serie de instrucciones colocadas en cierta
secuencia, necesarias para la descripción de las
operaciones que llevan a la solución de un
problema.
5.- Es un procedimiento completo para resolver un
problema específico en un número "FINITO" de
pasos.
6.- Es un método para resolver un problema
mediante una serie de datos precisos, definidos y
finitos.
PASOS PARA PLANTEAR LA SOLUCIÓN
A UN PROBLEMA:
1.- Análisis del problema.
2.- Identificar las entradas, procesos y salidas del
problema, declaración de variables.
3.- Diseño del Algoritmo: Describe la secuencia
ordenada de los pasos, sin ambigüedad, es decir, siendo
preciso y veraz en la búsqueda de la solución al
problema.
4.- Codificación del Algoritmo: Es la
expresión en un lenguaje de programación de los
pasos definidos en el algoritmo.
5.- Ejecución y validación del programa
por el computador.
CARACTERÍSTICAS DE
ALGORITMOS:
Las características fundamentales
que debe cumplir todo algoritmo son:
1.- Un algoritmo debe ser preciso e indicar el orden de
realización de cada paso.
2.- Un algoritmo debe estar bien definido, es decir, si
se sigue la ejecución dos veces del mismo se debe obtener
la misma secuencia lógica. El algoritmo debe definirse de
forma precisa para cada paso, es decir, hay que evitar toda
ambigüedad al definir cada paso. Puesto que el lenguaje
humano es impreciso, los algoritmos se expresan mediante un
lenguaje formal, ya sea matemático o de
programación para un computador.
3.- Un algoritmo debe ser "FINITO", Si se
sigue un algoritmo se debe terminar en algún momento; o
sea, debe tener un numero finito de pasos.
4.- Entrada: El algoritmo
tendrá cero o más entradas, es decir, cantidades
dadas antes de empezar el algoritmo. Estas cantidades pertenecen
además a conjuntos especificados de objetos. Por ejemplo,
pueden ser cadenas de caracteres, enteros, naturales,
fraccionarios, etc. Se trata siempre de cantidades
representativas del mundo real expresadas de tal forma que sean
aptas para su interpretación por el computador.
5.- Salida: El algoritmo tiene
una o más salidas, en relación con las
entradas.
CLASIFICACIÓN DE LOS
ALGORITMOS:
Directos: Son aquellos que permiten encontrar la
solución al problema de manera instántanea o
directa, en un número determinado de pasos.
Ejemplo: 23 = 2*2*2 = 8
Indirecto:
a) Se ignora el número de
pasos.b) Son aquellos donde se desconocen el
número de pasos para lograr la solución de un
problema.
Estos a su vez, se clasifican en:
Finito: El número de pasos a realizar son
conocidos así como la factibilidad de solución al
problema planteado, o sea, que va a ver una respuesta al
proceso.
Ejemplo:
Medir distancia

Es factible que algún día pueda saber la
distancia entre la Sede antigua del IUTEPAL (Av.
Constitución) y la Sede Nueva del IUTEPAL (Urb.
Caña de Azúcar).
Infinito:
Se desconoce el número de pasos a realizar,
así como la imposibilidad de encontrar la solución
al problema planteado.
Cuando realmente es imposible lograr la solución,
por más vueltas que le demos al problema.
Ejemplo:

Ejemplos de Algoritmos:
Podemos idear un algoritmo para un determinado proceso,
así como también hacerlo en diferentes
formas.
Por ejemplo: Cómo podríamos encontrar el
promedio de un conjunto de números?.
Una posible solución sería:
1.- Sumar los números dados.
2.- Contar dichos números.
3.- Dividir el resultado obtenido en el punto 1 entre el
resultado obtenido en el punto 2.
Otra clase de ejemplo de Algoritmos, sería el de
una llamada telefónica, o el proceso para efectuar un
viaje en el Metro de Caracas, o la obtención de la
licencia para conducir o el cambio de un caucho que esté
bajo de aire, etc; en fin, hay muchas formas de aplicar los
algoritmos en cuestiones cotidianas descomponiendo la
acción en pasos lógicos, como es el caso de una
llamada desde una cabina de un teléfono
público:
1.- Inicio
2.- Descolgar el teléfono
3.- Esperar la señal digital.
4.- Preguntamos si está dañado. Si lo
está: Vamos al paso 5.
Si no lo está: Vamos al paso 8.
5.- Vociferar una palabra de mal gusto y fruncir el
ceño.
6.- Colgar.
7.- Fin.
8.- Digitar los números.
9.- Verificamos si suena ocupado. Si suena ocupado:
Vamos al paso 11.
Si no lo está: Vamos al paso 13.
10.-Insistir digitando los números.
11.- Ir al paso 8.
12.- Verificamos si contestan. Si contestan: Vamos al
paso 14
Si no contestan: Vamos al paso 21.
13.- Preguntamos si se encuentra la persona.
Si se encuentra: Vamos al paso 14.
Si no se encuentra: Vamos al paso 17.
14.- Hablar lo deseado.
15.- Colgar.
16.- Fin.
17.- Pensar algo malo.
18.- Tomar un café y tranquilizarse.
19.- Ir al paso 15.
A continuación, presentamos un ejemplo de
algoritmo para el proceso de cambiar un caucho que está
bajo de aire.
1.- Levantar el carro con el gato
hidraúlico.
2.- Quitar los tornillos del rin.
3.- Quitar el caucho dañado.
4.- Poner el caucho de repuesto.
5.- Apretar los tornillos.
6.- Bajar el carro con el gato.
A los anteriores pasos, podríamos agregar muchos
más detalles como por ejemplo, abrir la maleta, aflojar
tornillos antes de levantar el carro, etc. Presentamos a
continuación, dos versiones mas amplias del algoritmo
anterior:
Versión Nº 1
1.- Sacar el caucho de repuesto y herramientas de la
maletera.
2.- Verificamos si está dañado el caucho
de repuesto.
Si lo está vamos al punto 3.
Si no lo está vamos al punto 4.
3.- Vociferamos ruidosamente algo.
Nos vamos caminando a buscar ayuda ó telefoneamos
alguien para que ayude.
Vamos al punto 14.
4.- Verificamos si el caucho bajo de aire es el caucho
delantero. Si lo es:
4.1.- Quitamos la tapa del centro de la rueda
delantera.
4.2.- Aflojamos los tornillos.
4.3.- Levantamos el carro por delante, junto al caucho
dañado.
4.4.- Vamos al punto 5.
Si no lo es:
4.1.- Quitamos la tapa del centro de la rueda
trasera.
4.2.- Aflojamos los tornillos.
4.3.- Levantamos el carro por detrás, junto al
caucho dañado.
5.- Quitamos los tornillos.
6.- Quitamos el caucho dañado.
7.- Ponemos el caucho de repuesto.
8.- Colocamos los tornillos y las tapas.
9.- Bajamos el carro con el gato
hidraúlico.
10.- Guardamos el caucho dañado, el gato y las
herramientas en la maletera.
11.- Nos limpiamos con estopa las manos.
12.- Encendemos el vehículo.
13.- Continuamos manejando.
14.- Fin.
Versión Nº 2
1.- Observamos si el caucho de repuesto está
vacío.
Si lo está vamos al punto 2.
Si no lo está vamos al punto 3.
2.- Llamamos a un taller.
Vamos al punto 12.
3.- Levantamos el carro con el gato
hidráulico.
4.- Quitamos un tornillo.
5.- Observamos si hemos quitado todos los
tornillos.
Si lo hemos quitado vamos al punto 6.
Si no lo hemos quitado vamos al punto 4.
6.- Quitamos el caucho dañado.
7.- Ponemos el caucho de repuesto.
8.- Apretamos un tornillo.
9.- Verificamos si se han apretado todos los
tornillos.
10.- Si lo hemos apretado, vamos al punto 11.
Si no lo hemos apretado vamos al punto 8.
11.- Bajamos el carro con el gato
hidráulico.
12.- Fin.
Descripción de un algoritmo en
forma gráfica:
Cuando una secuencia de actividades que definen un
problema es muy simple en su naturaleza, es decir que sólo
implique seguir una serie de pasos, uno después de otro, y
que no tenga decisiones lógicas ni alternativas a tomar,
es muy fácil describirlo en palabras. Pero si esta
secuencia de actividades se hace más compleja será
no sólo difícil describirlo en palabras sino
también retener todas las alternativas.
Para ilustrar lo anterior, analicemos la secuencia de
eventos que tienen lugar todas las mañanas para un
estudiante de Universidad que tiene clase los lunes y los
miércoles a las 08:00 am y los martes y jueves a las 09:00
am.
Una vez que el estudiante se despierta mira el reloj y
si no son aún las 06:30 am, continúa durmiendo. Los
lunes y los miércoles, procura levantarse entre las 06:30
am y las 07:30 am. Si llegara a despertarse después de la
hora como frecuentemente ocurre, pensará nuevamente en la
falta que le hace el reloj despertador, pero toma la
decisión de no ir a clases en esa mañana, sin
embargo, después de esta decisión, se baña,
se desayuna y se dedica a estudiar.
Si se despierta entre las 06:30 am y las 07:30 am, los
lunes o los miércoles se baña, se desayuna y se
dedica a leer el periódico hasta que sean más de
las 07:30 am, luego toma el bus y llega a la Universidad. Entra a
clase solamente si han transcurrido menos de 15 minutos desde su
comienzo, de otra manera, no entra a clase y se dedica a leer las
carteleras y a esperar la próxima clase.
Los martes y los jueves, procura levantarse entre las
07:30 am y las 08:30 am; si se despierta después de las
08:30 am realizará las mismas actividades que
tendrían lugar si se levantara los lunes o los
miércoles después de las 07:30 am. De otra forma se
baña, se desayuna y lee el periódico hasta que sean
más de las 08:30 am, luego realiza las mismas actividades
que tienen lugar los lunes o lo miércoles cuando sale de
su casa.
Los demás días de la semana, procura
dormir hasta las 08:30 am, después de esta hora se
baña, se desayuna y se dedica a estudiar.
Es dudoso que quien lea por primera vez lo anterior
esté en capacidad de seguir y mantener fielmente en su
memoria la cantidad de actividades, secuencias, decisiones y
alternativas que tiene el ejemplo. Su respuesta obvia para
remediar lo anterior será dibujar un gráfico, y aun
sin conocer todas las técnicas de los diagramas de flujo
será mucho más fácil para una persona seguir
las actividades a través de un gráfico.
Algoritmos computacionales
Es importante el estudio y conocimiento de lo que hoy
conocemos como Algoritmos Computacionales, que desde su
aparición hasta nuestros días es, y seguirá
siendo; vital para el desarrollo de aplicaciones para
computadoras y el manejo y dominio de la lógica de
programación para resolver problemas.
Marco Histórico
Un algoritmo es un conjunto de operaciones
y procedimientos que deben seguirse para resolver un problema. La
palabra algoritmo se deriva del nombre latinizado del gran
Matemático Árabe Mohamed Ibn Al Kow Rizmi, el cual
escribió sobre los años 800 y 825 su obra Quitad Al
Mugabala, donde se recogía el sistema de numeración
hindú y el concepto del cero. Fue Fibinacci, el que
tradujo la obra al latín y el inicio con la palabra:
Algoritmi Dicit.El lenguaje algorítmico es aquel por medio
al cual se realiza un análisis previo del problema a
resolver y encontrar un método que permita resolverlo. El
conjunto de todas las operaciones a realizar y e orden en que se
deben efectuarse, se le denomina algoritmo.
Generalidades
El programador de computadoras es ante que nada una
persona que resuelve problemas, por lo que para llegar a ser un
programador eficaz se necesita aprender a resolver problemas de
un modo riguroso y sistemático. A la metodología
necesaria para resolver problemas mediante programas se denomina
Metodología de la Programación. El eje central de
esta metodología es el concepto, ya tratado, de
algoritmo.
Un algoritmo es un método para resolver un
problema. Aunque la popularización del término ha
llegado con el advenimiento de la era informática,
algoritmo proviene de Mohammed al-Khowarizmi, matemático
persa que vivió durante el siglo IX y alcanzo gran
reputación por el enunciado de las reglas para sumar,
restar, multiplicar y dividir números decimales; la
traducción al latín del apellido de la palabra
algorismus derivo posteriormente en algoritmo. Euclides, el gran
matemático griego (del siglo IV antes de Cristo) que
invento un método para encontrar el máximo
común divisor de dos números, se considera con
Al-Khowarizmi el otro gran padre de la algoritmia (ciencia que
trata de los algoritmos).
El profesor Niklaus Wirth, inventor de
Pascal, Modula-2 y Oberon, titulo uno de sus mas famosos libros,
Algoritmos + Estructuras de Datos = Programas,
significándonos que solo se puede llegar a realizar un
buen programa con el diseño de un algoritmo y una correcta
estructura de datos. Esta ecuación será de una de
las hipótesis fundamentales consideradas en esta obra.La
resolución de un problema exige el diseño de un
algoritmo que resuelva el problema propuesto.
Los pasos para la resolución de un problema
son:
Diseño de algoritmo, que describe la
secuencia ordenada de pasos que conducen a la solución
de un problema dado. (Análisis del problema y
desarrollo del algoritmo).Expresar el algoritmo como un programa de lenguaje
de programación adecuado. (Fase de
codificación.)Ejecución y validación
del programa por la computadora.
Para llegar a la realización de un
programa es necesario el diseño previo de algoritmo, de
modo que sin algoritmo no puede existir un programa.Los
algoritmos son independientes tanto del lenguaje de
programación en que se expresan como de la computadora que
lo ejecuta. En cada problema el algoritmo se puede expresar en un
lenguaje diferente de programación y ejecutarse en una
computadora distinta; sin embargo, el algoritmo será
siempre el mismo. Así, por ejemplo, en una analogía
con la vida diaria, una receta de un plato de cocina se puede
expresar en español, ingles o francés, pero
cualquiera que sea el lenguaje, los pasos para la
elaboración del plato se realizaran sin importar el idioma
del cocinero.
En la ciencia de la computación y en
la programación, los algoritmos son más importantes
que los lenguajes de programación o las computadoras. Un
lenguaje de programación es tan solo un medio para
expresar un algoritmo y una computadora es solo un procesador
para ejecutarlo. Tanto el lenguaje de programación como la
computadora son los medios para obtener un fin: conseguir que el
algoritmo se ejecute y se efectúe el proceso
correspondiente.Dada la importancia del algoritmo en la ciencia
de la computación, un aspecto muy importante será
el diseño de algoritmos. El diseño de la
mayoría de los algoritmos requiere creatividad y
conocimientos profundos de la técnica de la
programación. En esencia, la solución de un
problema se puede expresar mediante un algoritmo.
La definición de un algoritmo debe definir tres
partes: Entrada, Proceso y Salida. En el algoritmo de receta de
cocina citado anteriormente se tendrá:
Entrada: ingrediente y utensilios
empleados.
Proceso: elaboración de la receta en la
cocina.
Salida: terminación del plato (por
ejemplo, cordero).
Ejemplo de Algoritmo:Un cliente ejecuta un
pedido a una fábrica. Esta examina en su banco de datos la
ficha del cliente; si el cliente es solvente entonces la empresa
acepta el pedido; en caso contrario rechazara el pedido. Redactar
el algoritmo correspondiente.Los pasos del algoritmo
son:
inicio
leer el pedido
examinar la ficha del
clientesi el cliente es solvente aceptar
pedido; en caso contrario, rechazar pedidofin
Diseño del Algoritmo:En la
etapa de análisis del proceso de programación se
determina que hace el programa. En la etapa de diseño se
determina como hace el programa la tarea solicitada. Los
métodos mas eficaces para el proceso de diseño se
basan en el conocido por Divide y Vencerás, es decir, la
resolución de un problema complejo se realiza dividiendo
el problema en sub problemas y a continuación dividir
estos sub problemas en otros de nivel mas bajo, hasta que pueda
ser implementada una solución en la computadora. Este
método se conoce técnicamente como diseño
descendente (Top Down) o modular. El proceso de romper el
problema en cada etapa y expresar cada paso en forma más
detallada se denomina refinamiento sucesivo.
Cada sub programa es resuelto mediante un
modulo (sub programa) que tiene un solo punto de entrada y un
solo punto de salida.Cualquier programa bien diseñado
consta de un programa principal (el modulo de nivel mas alto) que
llama a sub programas (módulos de nivel mas bajo) que a su
vez pueden llamar a otros sub programas. Los programas
estructurados de esta forma se dice que tienen un diseño
modular y el método de romper el programa en
módulos más pequeño se llama
Programación Modular. Los módulos pueden ser
planeados, codificados, comprobados y depurados
independientemente (incluso por diferentes programadores) y a
continuación combinarlos entre si. El proceso implica la
ejecución de los siguientes pasos hasta que el programa se
termina:
Programar módulo.
Comprobar el módulo.
Si es necesario, depurar el
modulo.Combinar el modulo con los
módulos anteriores.
El proceso que convierte los resultados del
análisis del problema en un diseño modular con
refinamiento sucesivo que permitan una posterior
traducción al lenguaje se denomina diseño de
algoritmo.
El diseño del algoritmo es independiente del
lenguaje de programación en el que se vaya a codificar
posteriormente.
5. Técnica de diseño de
algoritmos
Diseño de Algoritmos: Hasta ahora se
han realizado algunos comentarios respecto a la necesidad de
diseñar algoritmos correctos y eficientes utilizando los
elementos de un lenguaje de programación .Es necesario en
este momento mencionar algo sobre como hacerlo. El acto de
diseñar un algoritmo puede considerarse como una tarea que
difícilmente podrá ser del todo
automatizada.
Todo problema algorítmico es un reto para su
diseñador, algunos resultan inmediatos de resolver, otros
son bastante complejos. La investigación en esta
área ha permitido descubrir un conjunto de métodos
o esquemas de diseño hacia los cuales puede orientarse la
realización de muchos algoritmos.No obstante, y a pesar de
que resulta mas adecuado en bastantes casos utilizar alguno de
estos esquemas que realizar un diseño desde cero, idear un
algoritmo continua siendo una labor bastante creativa donde los
conocimientos y la experiencia del propio diseñador tiene
un papel fundamental.
El diseño de un algoritmo que resuelva un
problema es, en general, una tarea difícil. Una forma de
facilitar esta labor consiste en recurrir a técnicas
conocidas de diseño de algoritmos, se decir, a esquemas
muy generales que pueden adaptarse a un problema particular al
detallar las partes generales del esquema.
Muchos problemas pueden resolverse buscando una
solución fácil y directa pero, a la vez bastante
ineficiente. Este método, llamado de fuerza bruta, puede
ser muy directo, pero con un poco de análisis puede
encontrarse algoritmos más eficientes. El esquema mas
sencillo quizás sea el llamado divide y vencerás,
basado en la descomposición de un problema en
subproblemas.
Otros esquemas requieren un análisis minucioso
del problema de forma que la solución se vaya construyendo
en etapas. Si puede preverse que decisión conviene en cada
etapa para producir cierto tipo de mejor resultado, tenemos una
solución voraz, si la decisión en una etapa, solo
puede tomarse tras considerar varias soluciones de otras etapas
mas simples, la solución es dinámica. Aun
así, hay problemas cuya solución no puede hallarse
sino mediante un proceso de búsqueda, a pesar de lo
complejas que son las operaciones de búsqueda, su uso
adecuado mediante el esquema de búsqueda con retroceso (o
backtracking) permite ganar gran eficiencia respecto a soluciones
de fuerza bruta.
Por ultimo, conviene conocer otros métodos de
diseño de algoritmos que también resultan de
utilidad práctica. Nos estamos refiriendo a métodos
basados en la mejora de la eficiencia (por ejemplo, el uso de
parámetros de acumulación al resolver problemas
utilizando divide y vencerás, y el empleo de tablas como
estructura auxiliar para la resolución eficiente de
problemas donde se aplica programación dinámica), y
a métodos basados en transformaciones del dominio para
encontrar una solución mas fácilmente a un problema
en un dominio transformado, siendo dicha solución
finalmente adaptada al dominio original.
Consideraciones generales:Si el
hábil programador dispone de un recetario de algoritmos de
donde poder seleccionar el más adecuado para cada
problema, su tarea se simplifica. Supongamos que disponemos de
una especificación precisa, completa y consistente del
problema a resolver y queremos obtener un algoritmo en el que,
dados uno datos de entrada valido, se produzca cierto resultado.
Si no nos importa la eficiencia del algoritmo, podríamos
utilizar un algoritmo general llamado algoritmo del museo
británico. Se programa un computador de manera que parta
de un conjunto de axioma matemáticos y los que use para
reducir aleatoriamente teoremas validos.
Aprender los principios básicos del diseño
de algoritmos podemos preguntarnos por un método
aceptable. El mas entendido, y quizás el mejor, es
organizar el diseño sobre un esquema de algoritmo o una
técnica de diseño que haya demostrado su utilidad
para otros problemas. Este método de trabajo es
practicable, puesto que existe un número reducido de
esquema y técnicas de diseño.
El conocimiento de técnicas de diseño es
solo un primer paso para el diseñador, que debe
completarse con otros conocimientos y, sobre todo, con la
experiencia.
A menudo los algoritmos requieren una
organización bastante compleja de los datos, y es por
tanto necesario un estudio previo de las estructuras de datos
fundamentales. Dichas estructuras pueden implementarse de
diferentes maneras, y es más, existen algoritmos para
implementar dichas estructuras. El uso de estructuras de datos
adecuadas pueden hacer trivial el diseño de un algoritmo,
o un algoritmo muy complejo puede usar estructuras de datos muy
simples.
Uno de los algoritmos más antiguos conocidos es
el algoritmo de Euclides. El término algoritmo proviene
del matemático Muhammad ibn Musa al-Khwarizmi, que
vivió aproximadamente entre los años 780 y 850 d.C.
en la actual nación Iraní. El describió la
realización de operaciones elementales en el sistema de
numeración decimal. De al-Khwarizmi se obtuvo la
derivación algoritmo.
– Clasificación de algoritmos
* Algoritmo determinista: en cada paso del
algoritmo se determina de forma única el siguiente
paso.
* Algoritmo no determinista: deben decidir
en cada paso de la ejecución entre varias alternativas y
agotarlas todas antes de encontrar la solución.
Todo algoritmo tiene una serie de
características, entre otras que requiere una serie de
recursos, algo que es fundamental considerar a la hora de
implementarlos en una máquina.
Estos recursos son principalmente:
· El tiempo: período transcurrido
entre el inicio y la finalización del algoritmo.·
La memoria: la cantidad (la medida varía según la
máquina) que necesita el algoritmo para su
ejecución.
Obviamente, la capacidad y el diseño de la
máquina pueden afectar al diseño del
algoritmo.
En general, la mayoría de los problemas tienen un
parámetro de entrada que es el número de datos que
hay que tratar, esto es, N. La cantidad de recursos del
algoritmo es tratada como una función de N. De esta manera
puede establecerse un tiempo de ejecución del algoritmo
que suele ser proporcional a una de las siguientes
funciones:
1 : Tiempo de ejecución constante.
Significa que la mayoría de las instrucciones se
ejecutan una vez o muy pocas.logN : Tiempo de ejecución
logarítmico. Se puede considerar como una gran
constante. La base del logaritmo (en informática la
más común es la base 2) cambia la constante,
pero no demasiado. El programa es más lento cuanto
más crezca N, pero es inapreciable, pues logN no se
duplica hasta que N llegue a N2.N : Tiempo de ejecución lineal. Un
caso en el que N valga 40, tardará el doble que otro
en que N valga 20. Un ejemplo sería un algoritmo que
lee N números enteros y devuelve la media
aritmética.N·logN : El tiempo de ejecución
es N·logN. Es común encontrarlo en algoritmos
como Quick Sort y otros del estilo divide y vencerás.
Si N se duplica, el tiempo de ejecución es ligeramente
mayor del doble.N2 : Tiempo de ejecución
cuadrático. Suele ser habitual cuando se tratan pares
de elementos de datos, como por ejemplo un bucle anidado
doble. Si N se duplica, el tiempo de ejecución aumenta
cuatro veces. El peor caso de entrada del algoritmo Quick
Sort se ejecuta en este tiempo.N3 : Tiempo de ejecución
cúbico. Como ejemplo se puede dar el de un bucle
anidado triple. Si N se duplica, el tiempo de
ejecución se multiplica por ocho.2N : Tiempo de ejecución exponencial.
No suelen ser muy útiles en la práctica por el
elevadísimo tiempo de ejecución. El problema de
la mochila resuelto por un algoritmo de fuerza bruta -simple
vuelta atrás- es un ejemplo. Si N se duplica, el
tiempo de ejecución se eleva al cuadrado.
* Algoritmos polinomiales: aquellos que son
proporcionales a Nk. Son en general factibles.
* Algoritmos exponenciales: aquellos que son
proporcionales a kN. En general son infactibles salvo un
tamaño de entrada muy reducido.
– Notación O-grande
En general, el tiempo de ejecución es
proporcional, esto es, multiplica por una constante a alguno de
los tiempos de ejecución anteriormente propuestos,
además de la suma de algunos términos más
pequeños. Así, un algoritmo cuyo tiempo de
ejecución sea T = 3N2 + 6N se puede considerar
proporcional a N2. En este caso se diría que el algoritmo
es del orden de N2, y se escribe O(N2). Los grafos definidos por
matriz de adyacencia ocupan un espacio O(N2), siendo N el
número de vértices de éste.
La notación O-grande ignora los factores
constantes, es decir, ignora si se hace una mejor o peor
implementación del algoritmo, además de ser
independiente de los datos de entrada del algoritmo. Es decir, la
utilidad de aplicar esta notación a un algoritmo es
encontrar un límite superior del tiempo de
ejecución, es decir, el peor caso.
A veces ocurre que no hay que prestar
demasiada atención a esto. Conviene diferenciar entre el
peor caso y el esperado. Por ejemplo, el tiempo de
ejecución del algoritmo Quick Sort es de O(N2). Sin
embargo, en la práctica este caso no se da casi nunca y la
mayoría de los casos son proporcionales a N·logN.
Es por ello que se utiliza esta última expresión
para este método de ordenación.
Una definición rigurosa de esta
notación es la siguiente:

– Clasificación de
problemas
Los problemas matemáticos se pueden dividir en
primera instancia en dos grupos:
* Problemas indecidibles: aquellos que no se
pueden resolver mediante un algoritmo.
* Problemas decidibles: aquellos que cuentan
al menos con un algoritmo para su cómputo. Sin embargo,
que un problema sea decidible no implica que se pueda encontrar
su solución, pues muchos problemas que disponen de
algoritmos para su resolución son inabordables para un
computador por el elevado número de operaciones que hay
que realizar para resolverlos. Esto permite separar los problemas
decidibles en dos:
* intratables: aquellos para los que no es
factible obtener su solución.
* tratables: aquellos para los que existe al
menos un algoritmo capaz de resolverlo en un tiempo
razonable.
Los problemas pueden clasificarse también
atendiendo a su complejidad. Aquellos problemas para los
que se conoce un algoritmo polinómico que los resuelve se
denominan clase P. Los algoritmos que los resuelven son
deterministas. Para otros problemas, sus mejores algoritmos
conocidos son no deterministas. Esta clase de problemas se
denomina clase NP. Por tanto, los problemas de la clase
P son un subconjunto de los de la clase NP, pues
sólo cuentan con una alternativa en cada paso.
Diagramas de
flujo
Los diagramas de flujo son esquemas que representan
gráficamente un algoritmo por medio de los pasos de un
proceso, que se realizan para entender mejor al mismo y son
utilizados en programación, economía y procesos
industriales. Utilizan una series de símbolos con
significados especiales.
Un diagrama de flujo u organigrama es una
representación diagramático que ilustra la
secuencia de las operaciones que se realizan para conseguir la
solución de un problema y son usados normalmente para
seguir la secuencia lógicas de las acciones en el
diseño de problemas de computadoras y se dibujan
generalmente antes de comenzar a programar el código
frente a la computadora y una que se dibuja el diagrama de flujo,
llega hacer fácil escribir el programa en cualquier idioma
de alto nivel.
1.- Lógica dibujada.
2.- Es la representación gráfica de la
solución a un problema utilizando símbolos
predefinidos para su interpretación.
3.- Es la representación gráfica del
algoritmo.
4.- A nivel de programación es la
representación gráfica de lo que se desea que la
computadora realice.
5.- Son representaciones graficas de un algoritmo el
cual muestra los pasos o procesos a seguir para alcanzar la
solución de un problema. Es llamado diagramas de flujo
porque los símbolos utilizados se conectan por medio de
flechas para indicar la secuencia de una operación y son
también llamados flujogramas. Utilizan diversos
símbolos para representar operaciones
específicas.
Importancia de los Diagramas de
Flujo:
Es importante ya que ayuda a designar cualquier
representación gráfica de un procedimiento o parte
de ese, como su nombre lo indica representa el flujo de
información de un proceso.
Tipos de Diagramas:
Diagrama de Programa: Representa
gráficamente un método propuesto para la
solución de un problema determinado.
Diagrama de Sistema: Representa la
integración; interacción lógicas de los
elementos dentro de un sistema propuesto.
Diagrama de Procedimiento: Representa
gráficamente una operación o flujo de datos dentro
de un sistema.
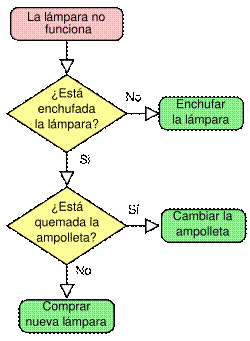
Diagrama de flujo sencillo con los pasos
a seguir si una lámpara no funciona.
Un diagrama de flujo es la forma más
tradicional de especificar los detalles algorítmicos de un
proceso. Se utiliza principalmente en programación,
economía y procesos industriales; estos diagramas utilizan
una serie de símbolos con significados especiales. Son la
representación gráfica de los pasos de un proceso,
que se realiza para entenderlo mejor. Son modelos
tecnológicos utilizados para comprender los rudimentos de
la programación lineal.
Definición
Es un esquema para representar gráficamente un
algoritmo. Se basan en la utilización de diversos
símbolos para representar operaciones específicas.
Se les llama diagramas de flujo porque los símbolos
utilizados se conectan por medio de flechas para indicar la
secuencia de operación.
Símbolos utilizados
Para poder hacer comprensibles los diagramas a todas las
personas, los símbolos se someten a una
normalización; es decir, se hicieron símbolos casi
universales, ya que, en un principio cada usuario podría
tener sus propios símbolos para representar sus procesos
en forma de Diagrama de flujo. Esto trajo como consecuencia que
sólo aquel que conocía sus símbolos, los
podía interpretar. La simbología utilizada para la
elaboración de diagramas de flujo es variable y debe
ajustarse a un patrón definido previamente.
En teoría, no es necesario usar un tipo especial
de símbolos para crear un diagrama de flujo, pero existen
algunos ampliamente utilizados por lo que es adecuado conocerlos
y utilizarlos, ampliando así las posibilidades de crear un
diagrama más claro y comprensible para crear un proceso
lógico y con opciones múltiples adecuadas. Se
utilizan los símbolos indicados a continuación,
estandarizados según la norma ISO 5807:
Flecha. Indica el sentido y trayectoria del proceso
de información o tarea.Rectángulo. Se usa para representar un evento
o proceso determinado. Éste es controlado dentro del
diagrama de flujo en que se encuentra. Es el símbolo
más comúnmente utilizado. Se usa para
representar un evento que ocurre de forma automática y
del cual generalmente se sigue una secuencia
determinada.Rectángulo redondeado: Se usa para
representar un evento que ocurre de forma automática
del cuál generalmente se sigue una secuencia
determinada.Rombo. Se utiliza para representar una
condición. Normalmente el flujo de información
entra por arriba y sale por un lado si la condición se
cumple o sale por el lado opuesto si la condición no
se cumple. El rombo además especifica que hay una
bifurcación.Círculo. Representa un punto de
conexión entre procesos. Se utiliza cuando es
necesario dividir un diagrama de flujo en varias partes, por
ejemplo por razones de espacio o simplicidad. Una referencia
debe darse dentro para distinguirlo de otros. La
mayoría de las veces se utilizan números en los
mismos.
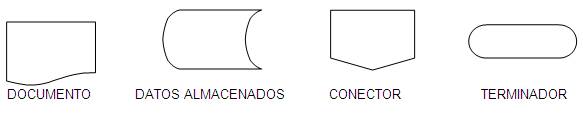
Existen además un sin fin de formas especiales
para denotar las entradas, las salidas, los almacenamientos,
etcétera.
De acuerdo al estándar ISO, los símbolos e
incluso las flechas deben tener ciertas características
para permanecer dentro de sus lineamientos y ser considerados
sintácticamente correctos. En el caso del círculo
de conexión, se debe procurar usarlo sólo cuando se
conecta con un proceso contenido dentro de la misma
hoja.
Existen también conectores de página, que
asemejan a una "rectángulo oblicuo" y se utilizan
para unir actividades que se encuentran en otra hoja.
Características que debe cumplir un
diagrama de flujo
En los diagramas de flujo se presuponen los siguientes
aspectos:
Existe siempre un camino que permite llegar a una
solución (finalización del
algoritmo).Existe un único inicio del
proceso.Existe un único punto de fin para el proceso
de flujo (salvo del rombo que indica una comparación
con dos caminos posibles).
Recomendaciones
A su vez, es importante que al construir diagramas de
flujo, se observen las siguientes recomendaciones:
Evitar sumideros infinitos, burbujas que tienen
entradas pero no salidas.Evitar las burbujas de generación
espontánea, que tienen salidas sin tener entradas,
porque son sumamente sospechosas y generalmente
incorrectas.Tener cuidado con los flujos y procesos no
etiquetados. Esto suele ser un indicio de falta de esmero,
pero puede esconder un error aún más grave: a
veces el analista no etiqueta un flujo o un proceso porque
simplemente no se le ocurre algún nombre
razonable.
VARIABLE: Es un valor no fijo que permanece
almacenado en la memoria del computador y que es identificado con
un nombre único y irrepetible.
Podemos definirlo como cualquier cantidad o valor al
cual hacemos referencia asignándole un nombre, clave (casi
siempre abreviada) y que tomará diferentes valores durante
el proceso.
Ejemplo: Nombres y Apellidos, Sueldo, Número de
Cédula de Identidad.
Físicamente, una variable es un espacio o
dirección en la memoria del computador.

CARACTERÍSTICAS DE LAS
VARIABLES:
El nombre de una variable puede ir formado por una o
más letras, números o la combinación de
ambas.

Los nombres de las variables siempre deberán
comenzar por una letra.

Los nombres de las variables no deberán ir
separados por espacios en blanco.Debe ser memotécnica.
Código Empleado = CODEMP
Cédula= CED
Sueldo= SDO
Impuesto sobre la Renta= ISLR
Seguro Social Obligatorio= SS0
Monto= MTO
TIPOS DE VARIABLES:
Alfanuméricas: Son aquellas que pueden
almacenar cualquier carácter, letras (A-Z);
números (0-9), espacios en blanco, o caracteres
especiales (¡ , %, *, + , /, $, &,
etc…)
Ejemplos:
ISLR= 10%
CED$= V-
&&.&&&.&&&
FEC= (__/__/__)
Numéricas: Son aquellas que almacenan
sólo números (Dígitos) de
(0-9).

CONSTANTE:
Es un valor que no varía, definido con un nombre
único y irrepetible que no va a cambiar durante todo el
algoritmo (Programa).
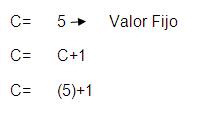
Es cualquier cantidad, la cual puede aparecer en forma
"LITERAL" y permanecerá invariable durante el proceso (Va
a almacenar un valor inalterable).
Ejemplos:
CONTADOR:
Es un valor que se incrementa o decrementa, según
sea el caso, un contador en términos constante es un valor
fijo que se va a ir contando, es decir cumpliendo una
función cuantitativa.
Es un campo en memoria, el cual sirve (como su nombre lo
indica) para contar, éste incrementa en el valor de 1 y
nos muestra el número de veces que el proceso ha detectado
una ocurrencia determinada y siempre deberemos expresarlo en
forma cuantitativa.
C= 0
Ejemplo:

ACUMULADOR:
Es un campo de memoria, un valor que se incrementa en
forma no definida esto por la suma de otro valor a dicho
campo.
Es un campo en memoria, pero que su incremento no es de
1, sino que viene alterándose por la suma de un valor a
dicho campo.
Ejemplo=

DECISIÓN:
Es una evaluación o determinación que va
arrojar un valor verdadero o falso.
Página siguiente  |