Acciones académicas para la consolidación de la enseñanza de la matemática (página 2)
Cuadro 1.
Operacionalización de la
Variable
Objetivo General. Proponer un plan basado
en acciones académicas que conduzca a la
consolidación de la enseñanza de la
matemática dirigido a los docentes del Liceo Bolivariano
"Capitanejo", ubicado en el municipio Ezequiel Zamora del estado
Barinas.
OBJETIVOS | VARIABLE | DIMENSIONES | INDICADORES | ITEMS | ||
Identificar qué acciones académicas Establecer la factibilidad del plan basado en Formular un plan basado en acciones | Enseñanza de la | Acciones |
| 1-2-3-4-5-6 7-8-9-10-11 12-13-14-15 | ||
Nota: Inédita. Ramírez
(2009)
CAPITULO III
Marco
metodológico
Tipo de
Investigación
El estudio se centra en la modalidad de un
proyecto factible; pues bien, la Universidad Pedagógica
Experimental Libertador (2003:7), señala "Consiste en la
elaboración de una propuesta de un modelo operativo viable
para solucionar problemas, requerimientos o necesidades de
organizaciones o grupos sociales"; en tal sentido, se propone un
plan basado en acciones académicas que conduzca a la
consolidación de la enseñanza de la
matemática dirigido a los docentes del Liceo Bolivariano
"Capitanejo", ubicado en el municipio Ezequiel Zamora del estado
Barinas.
En lo que respecta a la naturaleza de la
investigación, Namakforoosh (2002:91), sostiene: "La
investigación descriptiva es una forma de estudio para
saber quién, dónde, cuándo, cómo y
por qué del sujeto del estudio"; la verdad es que en el
presente trabajo, se buscó describir las acciones
académicas que asumen los docentes en la enseñanza
de la matemática.
Por su parte, la investigación es de campo; al
respecto, Sabino (2005:62), argumenta: "Conduce a la
obtención de los datos directamente de la realidad del
problema". Evidentemente que la información fue
recolectada por la autora del estudio de manera directa al
conocer las opiniones de los docentes en cuanto a las acciones
académicas que éstos desarrollan al enseñar
la matemática.
Procedimiento
Metodológico
Al tomar en cuenta el objetivo general del estudio y por
estar centrado en la modalidad de un proyecto factible, se asume
la posición de la Universidad Pedagógica
Experimental Libertador (UPEL) (2003:7), en lo concerniente a las
etapas que se deben desarrollar para ese tipo de proyecto, entre
las que destaca: "Diagnóstico, Factibilidad y
Diseño".
Fase I. Diagnóstico
En esta fase, se buscó una descripción de
la situación problemática, en cuanto a las acciones
académicas que asumen los docentes al enseñar la
matemática, etapa se caracterizó por hacer un
análisis de aspectos importantes como: población,
técnica e instrumento de recolección de datos,
validez, confiabilidad, procesamiento y análisis de
datos.
Fase II. Factibilidad
Los proyectos que se perfilan en un marco de la
factibilidad, éstos buscan producir un bien o servicio
para satisfacer una necesidad o colmar una expectativa; por tal
razón, en la evaluación técnica se
analizaron los tópicos referentes al comportamiento
disponible de los aspectos legal, técnico, institucional,
social y económico que hacen posible la estructura
operativa de la propuesta.
Fase III. Diseño de la
Propuesta
Esta fase, está relacionada con la
formulación de la propuesta en sí, que en este caso
es el plan basado en acciones académicas para la
enseñanza de la matemática. Aquí se plasman
las diferentes jornadas, cada una impregnada de objetivos
generales, específicos, contenidos, recursos tanto
materiales y humanos; así como, el tiempo necesario que se
requiere para el desarrollo de las actividades
programadas.
Población
En relación a este aspecto, Rizquel y otros
(2006:48), sostienen: "La población es el conjunto total
finito o infinito de elementos o unidades de observación
que se consideran en un estudio, nación, estado, grupos,
comunidades, objetos, instituciones, personas". Es así
como, la población quedó conformada por 10 docentes
especialistas en el área de matemática que laboran
en el Liceo Bolivariano "Capitanejo", ubicado en el municipio
Ezequiel Zamora del estado Barinas.
Técnicas e Instrumento de
Recolección de Datos
La técnica para la recolección de datos
que se utilizó en la presente investigación fue la
encuesta; al respecto, Rizquel y otros (2006:56), manifiestan:
"Son los recursos utilizados para facilitar la recolección
y el análisis de los hechos observados; éstos son
numerosos y varían de acuerdo con los factores a
evaluarse"; por consiguiente, se diseñó un
instrumento denominado cuestionario que midió la variable
enseñanza de la matemática; éste contiene
una portada de identificación, donde se recalca el
propósito del estudio, aparecen también as
instrucciones para su correcto llenado; asimismo, 15 ítems
que emergieron de las bases teóricas, junto a una escala
con tres alternativas de respuestas: siempre, algunas veces y
nunca. (Anexo A).
Validez del Instrumento
Para Scribano (2002:136), la validez "Es el grado en que
un instrumento refleja un dominio específico de contenido
de lo que se mide"; en tal sentido, la validación del
instrumento utilizado en el estudio se realizó a
través de la técnica juicio de expertos, cuyo
propósito se basó en determinar hasta qué
punto se media ciertamente la variable y dimensión para el
cual fueron diseñados. Evidentemente, para lograr lo
anterior, se seleccionaron los siguientes profesionales: dos
expertos en didáctica de la matemática y un
metodólogo a quienes se les fue entregada la
versión preliminar del instrumento, acompañados de
la respectiva información en cuanto a objetivos del
estudio, operacionalización de la variable, formato de
validación y síntesis curricular del especialista.
Una vez desarrollado el procedimiento anterior, el autor del
estudio se limitó a realizar un análisis exhaustivo
de las recomendaciones emitidas por los expertos, tomando en
cuenta las sugerencias propuestas para la elaboración del
cuestionario definitivo. (Anexo B)
Confiabilidad del
Instrumento
En cuanto a la confiabilidad, al tomar en
consideración las opiniones de Hernández y Otros
(2006:487), este proceso "Se refiere al grado en que su
aplicación repetida al mismo sujeto en objeto produce
igual resultado"; se tiene, que la confiabilidad se obtuvo a
través del procedimiento de cálculo del coeficiente
de confiabilidad Alpha de Cronbach para lo que se aplicó
una prueba piloto a 10 docentes no pertenecientes a la
población de estudio, pero sí con
características semejantes. El cálculo se
ejecutó por medio de la siguiente
ecuación.

El coeficiente alcanzado fue de 0,90 considerado de alta
magnitud, según la escala propuesta por Ruiz (2002).
(Anexo C)
Procesamiento y Análisis de los
Datos
Aplicados los cuestionarios a los 10 docentes del Liceo
Bolivariano "Capitanejo", ubicado en el municipio Ezequiel Zamora
del estado Barinas, el autor asumió las siguientes
acciones:
1. Revisión y organización de cada uno de
los cuestionarios aplicados.
2. Codificación con números de las
alternativas de respuestas: (3=Siempre), (2=Pocas Veces), y
(1=Nunca) emitidas por los docentes encuestados.
3. Elaboración de una matriz de doble entrada,
donde se tabularon las respuestas dadas por cada uno de los
docentes.
4. Uso de la estadística descriptiva con base a
las frecuencias absolutas y relativas; las expresiones
numéricas se obtuvieron a través de un computador y
del programa SPSS.
5. Los resultados obtenidos se confrontaron con las
bases teóricas desarrolladas en el marco
referencial.
CAPÍTULO IV
Análisis e
interpretación de los resultados
En el presente capítulo se observan los
resultados alcanzados durante la fase del diagnóstico una
vez aplicados los cuestionarios a los 10 docentes del Liceo
Bolivariano "Capitanejo", ubicado en el municipio Ezequiel Zamora
del estado Barinas, con el fin de describir qué acciones
académicas asumen los educadores en la enseñanza de
la matemática. Para el análisis e
interpretación de los datos se u tilizó la
técnica porcentual determinando las frecuencias absolutas
y relativas necesarias para llevar a cabo la intepretación
de los resultados; los mismo fueron presentados por indicadores
con sus respectivos cuadros y gráficos.
Cuadro 2
Distribución de frecuencias de los indicadores
correspondientes a la Variable: Enseñanza de la
Matemática. Dimensión: Acciones Académicas.
Indicador: Metodología en la
Enseñanza.
ITEMS | SIEMPRE | ALGUNAS VECES | NUNCA | ||||
1 | 3 | 30 | 7 | 70 | – | – | |
2 | 4 | 40 | 6 | 60 | – | – | |
3 | 2 | 20 | 7 | 70 | 1 | 10 | |
4 | – | – | 6 | 60 | 4 | 40 | |
5 | 4 | 40 | 5 | 50 | 1 | 10 | |
6 | 2 | 20 | 7 | 70 | 1 | 10 | |

Gráfico 1.
Dimensión: Acciones Académicas. Indicador:
Metodología en la Enseñanza
Al analizar la distribución de frecuencias en el
indicador Metodología en la Enseñanza, se tiene en
el (Ítem 1), que el 70% de los docentes afirmaron que
algunas veces abordan el arte de preguntar partiendo siempre del
lenguaje del estudiante y desde la duda en la construcción
de un conocimiento matemático; evidentemente, en el
(ítem 2), estos docentes señalaron en un 60% que
algunas veces conducen al estudiante a través de ejemplos
para el fomento de la discusión de un contenido
matemático; en tanto, en el (ítem 3), se obtuvo de
esta población en un 70% que algunas veces promueven la
curiosidad en el proceso de enseñanza de la
matemática; lo cierto es que en el (ítem 4), un 60%
de los docentes alegaron que algunas veces utilizan materiales
didácticos novedosos para favorecer auténticos
aprendizajes en el estudiante; de allí pues que, un 50% de
esta población aseguró en el (ítem 5), que
algunas veces emplean modelos didácticos fomentando la
investigación que permita el razonamiento lógico de
conceptos para que el estudiante llegue al saber
matemático; aunado a ello, se tiene en el (ítem 6),
que el 70% de los docentes expresaron que algunas veces presentan
al estudiante actividades matemáticas de cualquier tipo
para que tenga suficientes mecanismos de auto corrección.
Estos datos consolidan lo señalado por
Cuadro 3
Distribución de frecuencias de los indicadores
correspondientes a la Variable: Enseñanza de la
Matemática. Dimensión: Acciones Académicas.
Indicador: Educación basada en
Competencias.
ITEMS | SIEMPRE | ALGUNAS VECES | NUNCA | ||||
7 | 2 | 20 | 3 | 30 | 5 | 50 | |
8 | – | – | 4 | 40 | 6 | 60 | |
9 | 1 | 10 | 2 | 20 | 7 | 70 | |
10 | – | – | 3 | 30 | 7 | 70 | |
11 | – | – | 2 | 20 | 8 | 80 | |

Gráfico 2.
Dimensión: Acciones Académicas. Indicador:
Educación basada en Competencias
Para el indicador Educación basada en
Competencias, se tienen en el (item 7), que el 50% de la
población docente estudiada señaló que nunca
generan el razonamiento lógico del estudiante planteando
cuestiones propias de la matemática; aunado a ello, el 60%
de estos educadores en el (item 8), argumentaron que nunca
disponen de un sentido para la heurística partiendo del
por qué de los fenómenos matemáticos en la
clase; entre tanto, en el (item 9), el 70% de los docentes
alegaron que nunca promueven varias vías para comunicar
los contenidos matemáticos dentro de la clase; esto es
corroborado cuando en el (item 10), el 70% de los docentes
destacó que nunca traducen la realidad de la clase a una
estructura matemática; por ello, en el (item 11), el 80%
de estos educadores aseguró que nunca interpretan los
modelos matemáticos en términos reales. Los datos
arrojados afianzan lo expresado por
Cuadro 4
Distribución de frecuencias de los indicadores
correspondientes a la Variable: Enseñanza de la
Matemática. Dimensión: Acciones Académicas.
Indicador: Desarrollo de Habilidades.
ITEMS | SIEMPRE | ALGUNAS VECES | NUNCA | ||||
12 | – | – | 2 | 20 | 8 | 80 | |
13 | 1 | 10 | 2 | 20 | 7 | 70 | |
14 | 2 | 20 | 2 | 20 | 6 | 60 | |
15 | – | – | 3 | 30 | 7 | 70 | |

Gráfico 3.
Dimensión: Acciones Académicas. Indicador:
Desarrollo de Habilidades.
Finalmente, para el indicador Desarrollo de Habilidades,
(ítem 12), el 80% de los docentes exteriorizó que
nunca seleccionan actividades para que los estudiantes se
enfrenten a situaciones que les represente un reto; así
pues, en el (item 13), el 70% de los docentes consideraron que
nunca les da a los estudiantes la oportunidad de utilizar los
recursos con los que cuenta, es decir, no sugiere los
procedimientos que habrán de emplear.; de igual manera,
para el (item 14), el 60% declaró que nunca establecen
variantes didácticas que permitan facilitar o dificultar
la tarea, para que el estudiante se vea obligado a utilizar
recursos más elaborados; asimismo, en el (item 15), se
obtuvo que los educadores en un 70% expusieron que nunca dan a
conocer un número considerable de situaciones que puedan
plantear a los estudiantes de acuerdo al contenido
matemático a desarrollar. Esta información refuerza
una vez más lo destacado por
Conclusiones del
Diagnóstico
Al considerar el indicador Metodología en la
Enseñanza, se concluye como los educadores involucrados en
la investigación eventualmente abordan la técnica
de la pregunta al tomar en cuenta el lenguaje del estudiante y la
duda en la edificación del conocimiento matemático;
de modo que, en ciertos momentos se conduce al educando a la
discusión de contenidos matemático apoyados en
ejemplos, donde la curiosidad escasamente está presente.
De allí pues, hay carencias en cuanto a la
utilización de materiales didácticos novedosos que
permitan generar auténticos aprendizajes; desde luego, que
los modelos matemáticos pocas veces son llevados a la
práctica por los docentes; lo que conduce a que no se
generen verdaderas prácticas investigativas, en el marco
del razonamiento lógico de conceptos
matemáticos.
Entre tanto, para el indicador Educación basada
en Competencias, se infiere cómo los educadores no generan
cuestiones propias de la matemática para alcanzar el
razonamiento lógico que debe tener el estudiante. En
efecto, hay una carencia en la disposición de un sentido
para la heurística que le permita al estudiante razonar el
por qué de los fenómenos matemáticos, porque
prevalecen deficiencias en las formas o maneras de comunicar
contenidos, por lo que no hay una interpretación real de
los modelos matemáticos en términos
reales.
Finalmente, para el indicador Desarrollo de Habilidades,
se concluye como los docentes involucrados en la
investigación, insuficientemente escogen actividades para
que los educandos se enfrenten a situaciones que les representen
un reto para ellos, pues no se les da la oportunidad de utilizar
recursos propios en cuanto a los procedimientos que
deberán utilizar. Evidentemente, prevalecen fallas en
cuanto a la orientación de la enseñanza; hasta tal
punto, que los educadores no dan a conocer un número
considerable de situaciones que puedan plantear a los estudiantes
de acuerdo al contenido matemático a
desarrollar.
CAPÍTULO V
La
propuesta
Presentación
Un proyecto se genera con la existencia de un problema;
en tal sentido, se buscó reconocer en la presente
investigación una situación de interés,
dentro del contexto pedagógico del Liceo Bolivariano
"Capitanejo", en cuanto a identificar qué acciones
académicas asumen los docentes en la enseñanza de
la matemática. Esto representó un motivo para
realizar un análisis que conllevó a la
obtención de resultados y que permitió la toma de
una decisión sobre la consolidación de una
propuesta; en este caso, el diseño de un plan el cual es
definido como un conjunto integral de actividades teórico
y prácticas que buscan superar las debilidades
encontradas; de allí que, la estructura operativa se
caracteriza por tener el respaldo de objetivos de corte general,
específicos; así como también, contenidos,
actividades, lecturas reflexivas, dinámicas grupales,
recursos, tiempo y la evaluación de las
jornadas.
Factibilidad de la Propuesta
En esta fase del trabajo se precisa la factibilidad
legal, técnica, institucional, social y económica,
donde se da garantía a la viabilidad de la propuesta. A
continuación se hace la descripción de cada una de
ellas.
Factibilidad Legal
El plan basado en acciones académicas que
conduzca a la consolidación de la enseñanza de la
matemática dirigido a los docentes del Liceo Bolivariano
"Capitanejo", tiene su respaldo legal en la Constitución
de la República Bolivariana de Venezuela (1999) y en la
Ley orgánica de Educación (1980).
En ese orden de ideas, la Constitución de la
República Bolivariana de Venezuela (1999), en su
artículo 102, señala:
La Educación es un derecho humano y un deber
social fundamental, es democrática, gratuita y
obligatoria. El estado la asumirá como función
inclinable y de máximo interés en todos sus niveles
y modalidades, y como instrumento del conocimiento
científico, humanístico y tecnológico al
servicio de la sociedad. La Educación es un servicio
público y está fundamentada en el respeto a todas
las corrientes del pensamiento, con la finalidad de desarrollar
el potencial creativo de cada ser humano y el pleno ejercicio de
su personalidad en una sociedad democrática basada en la
valoración ética del trabajo y en la
participación activa, consciente y solidaria en los
procesos de transformación social. (p.87)
Está claro en la cita, el derecho que tienen los
venezolanos a recibir una educación de calidad y
ésta se debe caracterizar en un marco democrático,
gratuita y obligatoria, transformándose en un instrumento
fundamental para el desarrollo del país. Es de hacer
notar, que la praxis pedagógica se centra en el
conocimiento científico, humanístico y
tecnológico que requiere hoy día la sociedad; de
hecho, hay un marco amplio en el respeto de las diferentes
corrientes del pensamiento que busca el desarrollo integral de la
persona.
Si bien se debe destacar, la Ley orgánica de
Educación (1980) en su artículo 97, quien
alega:
El Ministerio de Educación, dentro de las
necesidades y prioridades del sistema educativo y de acuerdo con
los avances culturales, establecerá para el personal
docente programas permanentes de actualización de
conocimientos, especialización y perfeccionamiento con
estos programas, serán considerados en la
calificación de servicio (p.27).
Se observa del destacado artículo, que el
Ministerio de Poder Popular para la Educación, dentro de
sus prioridades debe generar programas de capacitación y
actualización de los docentes en servicio; todo esto, para
dar prioridad al mejoramiento de la praxis pedagógica que
desarrolla el docente en el aula de clase; de allí que, la
propuesta que se presenta en esta investigación se
justifica dentro del contexto legal porque se aspira de que el
docente de matemática se consolide en determinadas
acciones académicas en pro de mejorar la enseñanza
de esta importante asignatura que va a la par con el desarrollo
tecnológico de las sociedades.
Factibilidad Técnica
En lo que respecta a la factibilidad técnica de
la propuesta, se dispone de recursos humanos y materiales que
garantizan la operatividad del plan. Cabe destacar, que para el
desarrollo de los encuentros planificados se requiere de la
presencia de un especialista en didáctica de la
matemática; así como, del propio investigador
quienes están dispuestos a colaborar. Si bien es cierto,
la institución cuenta con recursos materiales como video
beam, pantalla, televisor, equipo de sonido, material de oficina,
sillas, mesas y un salón de usos múltiples en
excelentes condiciones.
Factibilidad Institucional
La factibilidad institucional, se comprueba por la
aceptación de los docentes objeto de estudio y quienes en
la actualidad se desempeñan en el aula de clase como
facilitadores del área de matemática y desde un
primer momento se encuentran interesados en conocer su realidad
en la manera de enseñar esta importante asignatura; de
allí su disposición de participar activamente en
las jornadas programadas en el plan de acción, partiendo
de la gran premisa que los grandes beneficiados serán
ellos y los propios estudiantes.
Factibilidad Social
El aprendizaje de la matemática, busca la
formación integral del estudiante al fomentar en
él, el desarrollo de habilidades y competencias que
facilitan la interpretación del ambiente que le rodea a
través de métodos que persiguen interpretar la
realidad sociocultural que envuelve al educando; de allí
que, los docentes se encuentran obligados a trabajar en
función de mejorar sus praxis pedagógicas al
enseñar la matemática; por lo que debe incorporar
operativamente acciones académicas que garanticen este
importante proceso. Por tal razón, el plan que se propone
puede ser ejecutado en otras instituciones del municipio Ezequiel
Zamora del estado Barinas que reflejen una situación
análoga a la aquí experimentada.
Factibilidad Económica
Los gastos económicos que emergen de la
aplicabilidad de la propuesta, serán financiados por los
docentes que facilitan la asignatura matemática y por el
autor del trabajo, quien desde un principio mantuvo una partida
especial para aquellos gastos que están vinculados al
desarrollo de las jornadas planificadas en la propuesta. Esta
información se ilustra en el siguiente cuadro.
CONCEPTO | VALOR (Bs.F) | |
Refrigerio. | 250,oo | |
Material fotocopiado. | 30,oo | |
Papel bond, lápices. | 30,oo | |
Honorarios del Ponente. | 400,oo | |
Total general: | 710,oo | |
Fuente: Inédita. Ramírez.
2009
Diseño de la
Propuesta
Evidentemente, que conocida la realidad en cuanto a las
acciones académicas que desarrollan los docentes del Liceo
Bolivariano "Capitanejo", al enseñar la matemática,
se reflejan una serie de debilidades en su accionar diario.
Así pues, el aprendizaje de la matemática se puede
sujetar a ciertas cualidades o atributos actitudinales que se
desprenden de la visión de los propios estudiantes en
relación con dicho objeto; por ello constituye, una de las
asignaturas de mayor complejidad en el proceso de
enseñanza; por lo que resulta difícil en la
práctica cotidiana. De allí la posición del
docente en asumir estrategias, actividades, métodos,
recursos y acciones propias que garanticen su forma o manera de
enseñar. Por tal razón, conocida la realidad en el
referido plantel, surge la propuesta de un plan que busca en
cierta medida superar la praxis pedagógica que se viene
desarrollando por parte de los docentes involucrados en el
estudio.
Estructura Operativa del
Plan
ENCUENTRO | ACCIÓN | TEMA | TIEMPO | ||
I. | Taller Teórico | Metodología en la | 6 Horas | ||
II | Taller Teórico | Educación basada en | 6 Horas | ||
III. | Taller Teórico | Desarrollo de | 6 Horas | ||
Fuente: Inédita. Ramírez.
(2009).


Objetivo Terminal: Finalizado el encuentro
los docentes estarán en capacidad de profundizar en
aquellas metodologías que garantizan la enseñanza
de la matemática.
Objetivo General: Sensibilizar a los
docentes sobre el manejo de metodologías en la
enseñanza de la matemática.


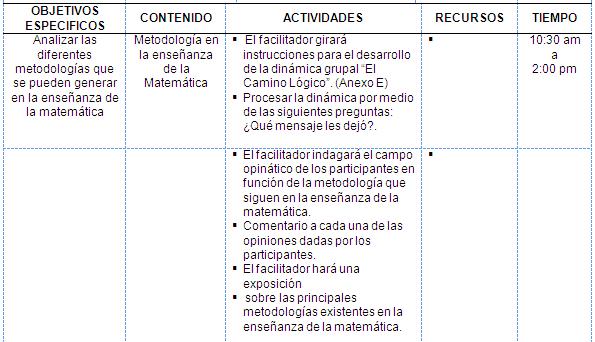



Objetivo Terminal: Terminado el encuentro
los docentes estarán en capacidad de ahondar en la
educación basada en competencias en la enseñanza de
la matemática.
Objetivo General: Concienciar a los docentes
sobre el abordaje de competencias en la enseñanza de la
matemática.
OBJETIVOS ESPECIFICOS | CONTENIDO | ACTIVIDADES | RECURSOS | TIEMPO | |||
Identificar las principales | Educación basada en |
|
| 8:00 am a 10:00 am | |||
OBJETIVOS ESPECIFICOS | CONTENIDO | ACTIVIDADES | RECURSOS | TIEMPO | |||
| |||||||
RECESO | 30 min | ||||||
OBJETIVOS ESPECIFICOS | CONTENIDO | ACTIVIDADES | RECURSOS | TIEMPO | |||
| 10:30 am a 2:00 pm | ||||||


Objetivo Terminal: Ejecutado el encuentro
los docentes estarán en capacidad de valorar el desarrollo
de las habilidades que se buscan en la enseñanza de la
matemática.
Objetivo General: Sensibilizar a los docentes
sobre la importancia de desarrollar habilidades en los
estudiantes en la enseñanza de la
matemática.
OBJETIVOS ESPECIFICOS | CONTENIDO | ACTIVIDADES | RECURSOS | TIEMPO | |||
Informar al docente de cómo | Desarrollo de |
|
| 8:00 am a 10:00 am | |||
OBJETIVOS ESPECIFICOS | CONTENIDO | ACTIVIDADES | RECURSOS | TIEMPO | |||
| |||||||
RECESO | 30 min | ||||||
OBJETIVOS ESPECIFICOS | CONTENIDO | ACTIVIDADES | RECURSOS | TIEMPO | |||
| |||||||
CAPÍTULO VI
Conclusiones y
recomendaciones
Conclusiones
No cabe duda que las acciones académicas en la
enseñanza de la matemática, desempeñan un
papel esencial, porque no basta con perfeccionar planes de
estudio, programas, libros de texto y otros materiales docentes;
también resulta decisiva la elevación de la calidad
de la labor del profesor y para ello ocupa un lugar destacado el
perfeccionamiento de todas aquellas actividades que están
vinculadas a los procedimientos, competencias y desarrollo de
habilidades.
En tal sentido, debido a como se desenvuelve el contexto
docente en la actualidad, un papel importante son los procesos
del pensamiento relacionado con el análisis,
síntesis, inducción, deducción,
abstracción entre otros; que apuntan a un trabajo
intelectual basado en el razonamiento en lugar de la
utilización rígida de la memoria a la cual
usualmente se recurre por parte de aquellos docentes que asumen
estilos de enseñanza memorísticos.
Sin embargo, el papel de la matemática tiene
justamente la finalidad de involucrar valores desarrollar
actitudes y aptitudes en el estudiante y se requiere para ello el
uso de lo ya reiterativo; acciones académicas que permitan
desarrollar las capacidades de comprender, asociar, analizar e
interpretar los conocimientos adquiridos para enfrentar el
entorno, a través de actitudes positivas.
Si bien es cierto, se resalta la importancia que tienen
las acciones académicas en la respectiva
planificación para la enseñanza de la
matemática; de manera que los estudiantes puedan tener
mayor visión y desenvolvimiento en la materia
práctica resultando así significativo y provechoso
para su vida, al mismo tiempo es relevante la preparación
del docente en el arte de planificar estrategias, recursos y
técnicas adecuadas para lo cual se debe contar con el
asesoramiento de personas especialistas y el desarrollo de
talleres evaluados para los educadores y a su vez que
éstos; sean conscientes de la responsabilidad que tienen
ante la sociedad: Educar con calidad.
En cuanto al diagnóstico de la realidad de los
docentes del Liceo Bolivariano "Capitanejo", se concluye que en
su mayoría en la praxis pedagógica al
enseñar la matemática escasamente promueven
acciones académicas que estén vinculadas a
metodologías de enseñanza novedosa que les permita
promover una educación basada en competencias y la
consolidación de desarrollar habilidades en el
estudiantado.
Recomendaciones
Difundir los resultados a todos los docentes del Liceo
Bolivariano "Capitanejo" con el fin de motivar a los educadores
que facilitan el área de matemática a que conozcan
la realidad que los circunda en cuanto a su praxis
pedagógica al enseñar esta importante
asignatura.
Ofrecer a los docentes involucrados en la
investigación talleres, charlas, conferencias, mesas de
discusión donde se les explique en profundidad las nuevas
acciones académicas que están imperando en los
escenarios actuales de la pedagogía en la enseñanza
de la matemática a fin de seguir verdaderas
metodologías donde se consolide la educación por
competencias y el desarrollo de destrezas en el
educando.
Desarrollar junto con los docentes involucrados en el
estudio, el método de experiencias donde se promuevan
vivencias significativas y auténticas en cuanto al empleo
de acciones académicas que garanticen una actividad
preactiva en la enseñanza de la matemática; porque
los beneficios directos en este aspecto, consolidan la
formación integral del estudiantado.
Se recomienda la incorporación del plan en el
Proyecto Educativo Integral Comunitario porque va a permitir a
los docentes conocer y manejar nuevas técnicas y recursos
a través de las acciones académicas que encierra la
propuesta, pues le servirá de ayuda cuando realicen la
planificación de actividades para luego aplicarlas en el
logro de aprendizajes efectivos en los escolares en cuanto a
matemática se refiere.
Referencia
bibliográficas
Chamoso, J. (2008). Hacia unas Nuevas
Matemáticas. Trabajo de ascenso publicado
Facultad de Educación. Universidad de Salamanca.
España.
Chevallard, G. (2005). Estudiar Matemáticas. El
Eslabón perdido entre Enseñanza y Aprendizaje.
México: Bosch
Constitución de la República
Bolivariana de Venezuela (1999). Gaceta Oficial de la
República de Bolivariana de Venezuela. N° 36869.
(Extraordinario) Diciembre 30, 1999.
González, J.; y Lupiáñez, L.
(2005). ¿Qué valor social tiene el
conocimiento matemático? Padres y Madres de
Alumnos. Revista de la CEAPA, No.82,
29-33.
Guzmán, M. (2007). Cuestiones
fundamentales de la enseñanza de la
Matemática. Revista Thales Nº 1 8,
p. 13-26.
Hernández, R.; Fernández, C.; y Baptista,
L. (2006). Metodología de la
Investigación. México: Mc.
Graw-Hill.
Kline, M. (2006) El fracaso de la Matemática
Moderna. México: Editorial Siglo XXI, S.A.
Ley Orgánica de Educación. (1980).
Gaceta Oficial N° 2635. Extraordinario, julio 26,
1980.
Namakforoosh, M. (2002). Metodología de la
Investigación. México: Limusa.
OCDE (2005). Informe PISA 2003.
Aprender para el mundo de mañana. Madrid:
Santillana.
Rico, L. (2005). La alfabetización
matemática y el Proyecto PISA de la
OCDE.
Padres y Madres de Alumnos. Revista de
la CEAPA, No. 82, 7-13.
Risquez, G.; Fuenmayor, E.; y Pereira, B. (2006).
Metodología de la Investigación I. Manual
Teórico Práctico. Universidad Rafael
Belloso Chapín URBE. Marcaibo. Zulia.
Rizo, C. (2006). La formación de
habilidades y capacidades en la enseñanza de las
matemáticas. Editorial Pueblo y Educación. La
Habana.
Ruiz, C. (2002). Instrumentos de
Investigación Educativa. Procedimientos para su
Diseño y Validación. Caracas. Venezuela:
CIDEG, C.A.
Sabino, C. (2005). El Proceso de
Investigación. Caracas. Venezuela:
Panapo.
Scribano, A. (2002). Introducción al
Proceso de Investigación en Ciencias Sociales.
Venezuela. Copiar.
Universidad Pedagógica Experimental Libertador.
(2006). Manual de Trabajos de Grado y Maestría y
Tesis Doctorales. Caracas. Venezuela.
FEDEUPEL
Anexos
REPÚBLICA BOLIVARIANA DE
VENEZUELA
UNIVERSIDAD VALLE DEL MOMBOY
DECANATO DE INVESTIGACIÓN Y
POSTGRADO
ESPECIALIZACIÓN DIDÁCTICA
DE LA MATEMÁTICA
Estimado Docente:
El presente cuestionario tiene como finalidad, obtener
información acerca de las acciones académicas que
asume el docente en la enseñanza de la matemática;
en tal sentido, se le agradece su meritoria colaboración
al responder con toda sinceridad los planteamientos formulados.
En caso de duda, consulte con el investigador.
Atentamente,
Lic. Giovanni Ramírez
INSTRUCCIONES
Para responder el cuestionario, lea cuidadosamente cada
pregunta y marque con una, "X", el recuadro que mejor refleje en
cuanto a su acción académica al enseñar la
matemática.
Nº | Ítems | Siempre | Algunas veces | Nunca | ||||||||||
1 | Aborda el arte de preguntar partiendo siempre del | |||||||||||||
2 | Conduce al estudiante a través de ejemplos | |||||||||||||
3 | Promueve la curiosidad en el proceso de | |||||||||||||
4 | Utiliza materiales didácticos novedosos | |||||||||||||
5 | Emplea modelos didácticos fomentando la | |||||||||||||
6 | Presenta al estudiante actividades | |||||||||||||
7 | Genera el razonamiento lógico del | |||||||||||||
8 | Dispone de un sentido para la heurística | |||||||||||||
9 | Promueve varias vías para comunicar los | |||||||||||||
10 | Traduce la realidad de la clase a una estructura | |||||||||||||
Nº | Ítems | Siempre | Algunas veces | Nunca | ||||||||||
11 | Interpreta los modelos matemáticos en | |||||||||||||
12 | Selecciona actividades para que los estudiantes se | |||||||||||||
13 | Les da a los estudiantes la oportunidad de | |||||||||||||
14 | Establece variantes didácticas que permitan | |||||||||||||
15 | Da a conocer un número considerable de | |||||||||||||
ANEXO B
VALIDACIÓN DEL INSTRUMENTO
FORMATO DE VALIDACION
Congruencia Item – Variable.
Escala: 1 = Deficiente 2 = Regular 3 = Bueno.
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |