Series de tiempo empleando Excel y Graph

1)
DEFINICIÓN

Las series de tiempo llamadas también series
cronológicas o series históricas son un conjunto de
datos numéricos que se obtienen en períodos
regulares y específicos a través del tiempo, los
tiempos pueden ser en años, meses, semanas, días o
otra unidad adecuada al problema que se esté trabajando.
Ejemplos de series de tiempo son: Ventas mensuales de un producto
en una empresa, producción total anual de petróleo
en Ecuador durante un cierto número años o las
temperaturas anunciadas cada hora por el meteorólogo para
un aeropuerto.

Matemáticamente, una serie de tiempo se define
por los valores Y1, Y2, Y3,…….de una variable Y
(ventas mensuales, producción total, etc.) en tiempos t1,
t3, t3……….. Si
se reemplaza a X por la variable tiempo, estas series se definen
como distribuciones de pares ordenados (X,Y) en el plano
cartesiano, siendo Y una función de X; esto se denota
por:

Y = f(t)?Y= f(X)

El principal objetivo de las series de tiempo es hacer
proyecciones o pronósticos sobre una actividad futura,
suponiendo estables las condiciones y variaciones registradas
hasta la fecha, lo cual permite planear y tomar decisiones a
corto o largo plazo. Después, con base en esa
situación ideal, que supone que los factores que
influyeron en la serie en el pasado lo continuarán
haciendo en el futuro, se analizan las tendencias pasadas y el
comportamiento de las actividades bajo la influencia de ellas;
por ejemplo, en la proyección de ventas de un producto o
de un servicio de una empresa se calculan los posibles precios,
la reacción del consumidor, la influencia de la
competencia, etc.

2) MOVIMIENTOS O
COMPONENTES

El modelo clásico o de descomposición,
considera que los datos de series de tiempo están
compuestas de los siguientes cuatro patrones
básicos:

2.1) TENDENCIA SECULAR

La tendencia secular o simplemente tendencia, son
movimientos o variaciones continuas de la variable de modo
uniforme y suave, por encima o por debajo, que se observan en el
largo plazo durante un período de longitud prolongada.
Representan el comportamiento predominante o dirección
general de la serie de tiempo como ascendente o descendente. La
gráfica de la tendencia suele ser una curva suave y aun
una línea recta que muestra la tendencia de las
variaciones. Ejemplos de tendencia secular son las ventas,
exportaciones, producción y el empleo.

La siguiente gráfica muestra la tendencia de
exportaciones de la Empresa D & M en período
2000-2009. Aunque los datos muestran ciertas variaciones
están por encima y por debajo de la recta de tendencia, la
tendencia secular es ascendente.

Empleando Excel:

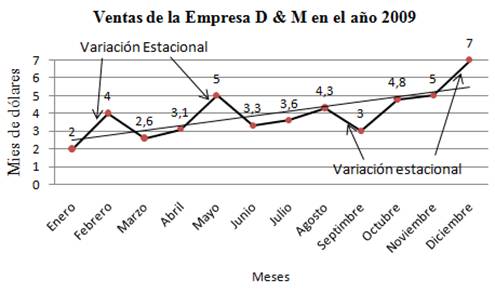
2.2) MOVIMIENTOS ESTACIONALES

Representa un movimiento periódico que se
producen en forma similar cada año por la misma
época, en correlación con los meses o con las
estaciones del año y aun con determinadas fechas. Si los
sucesos no se repiten anualmente, los datos deben recolectarse
trimestral, mensual o incluso semanalmente. Ejemplos de
movimientos estacionales son la variación de precios de
ciertos productos, incremento de ventas de juguetes y
disminución de ventas de útiles Navidad, incremento
de ventas de flores por el día del amor y la amistad,
etc.

A continuación se muestra un ejemplo de
gráfica que representa este tipo de movimientos
estacionales:

2.3) MOVIMIENTOS CÍCLICOS

Son variaciones hacia arriba y hacia abajo de la
tendencia que se presentan cada cierto número de
intervalos, en forma periódica de manera ondular a modo de
oscilaciones más o menos regulares durante un
período relativamente prolongado, que por lo general
abarca tres o más años de duración. La
producción, empleo, promedio industrial, etc. son ejemplos
de este tipo de movimientos.

A continuación se muestra un ejemplo de
gráfica que representa este tipo de movimientos
cíclicos:

2.4) MOVIMIENTOS IRREGULARES O
ALEATORIOS

Son aquellas variaciones producidas por sucesos de
ocurrencia imprevisible o accidental que producen movimientos sin
un patrón discernible; así por ejemplo, las
exportaciones de una empresa pueden ser afectadas por sucesos
inusuales no previsibles tales como huelgas, guerras, terremotos,
inundaciones, etc. Estas variaciones irregulares son de corta
duración y de magnitud muy variable.

A continuación se muestra un ejemplo de
gráfica que representa este tipo de movimientos
irregulares:

TAREA DE
INTERAPRENDIZAJE

1) Realice un organizador gráfico sobre las
series de tiempo.

2) Elabore empleando Excel las gráficas de los
ejemplos presentados en los movimientos estacionales,
cíclicos e irregulares.

3) Cree y elabore una gráfica que represente a
cada uno de los movimientos de las series de tiempo de manera
manual y empleando Excel.

3) MODELOS DE
SERIES DE TIEMPO

Son expresiones matemáticas de relación
entre los movimientos de tendencia secular (T), movimientos
cíclicos (C), movimientos estacionales (E) y movimientos
irregulares (I) que generan la variable Y. Hay dos modelos para
la definición de Y, los cuales son:

3.1) MODELO MULTIPLICATIVO

En el que Y queda definida por el producto de las
variaciones.

Y =
T·C·E·I

3.2) MODELO ADITIVO

En el que Y queda definida por la suma de las
variaciones.

Y = T + C + E + I

En el modelo multiplicativo, las variaciones se expresan
en términos relativos o porcentuales de la tendencia, en
tanto que en el modelo aditivo las variaciones se expresan como
residuos en las mismas unidades originales. El modelo aditivo
sufre el supuesto irreal de que los movimientos o componentes son
independientes uno de otro, algo que difícilmente se da en
el caso de la vida real. El modelo multiplicativo supone que los
movimientos o componentes interactúan entre sí y no
se mueven independientemente, por lo que este modelo es
más utilizado que el aditivo. Sin embargo, el criterio
fundamental que se debe seguir en el caso de una situación
dada es emplear el modelo que mejor se ajuste a los
datos.

4) MÉTODOS
DE SUAVIZAMIENTO Y PRONÓSTICO

Estos métodos eliminan las
fluctuaciones aleatorias de la serie de tiempo, proporcionando
datos menos distorsionados del comportamiento real de
misma.

4.1) MÉTODO DE LOS PROMEDIOS
MÓVILES

El movimiento medio de orden N de una serie
de valores Y1, Y2, Y3,… Yn se define por la sucesión de
valores correspondientes a las medias
aritméticas:

O sea los valores 7, 12

Nota:

Utilizando adecuadamente estos movimientos medios se
eliminan los movimientos o variaciones estacionales,
cíclicas e irregulares, quedando sólo el movimiento
de tendencia. Este método presenta el inconveniente de que
se pierden datos iniciales y finales de la serie original.
También se puede observar que a medida que N crece, la
cantidad de nuevos datos se reduce.

Si se emplean medias aritméticas ponderadas
en el método de los promedios móviles, el
método toma de nombre Promedios Móviles
Ponderados de Orden N.

Ejemplo ilustrativo

Con los siguientes datos acerca de la
ventas en miles de dólares de la Empresa D & M durante
los últimos 3 años tomados en períodos de
trimestres:

1) Suavizar los datos empleando el
método de los promedios móviles de orden 3
(longitud de 3 períodos).

2) Pronosticar las ventas para el trimestre
número 13.

3) Suponga que para el Gerente de Ventas la
última venta realizada es el doble de importante que la
penúltima, y la antepenúltima venta tiene la mitad
de importancia que la penúltima. Realizar el
pronóstico de ventas para el trimestre número 13
empleando el método de los promedios móviles
ponderados de orden 3.

4) Elaborar un gráfico en el que consten las
ventas y los promedios móviles (ventas
suavizadas).

Solución:

1) El cálculo de los promedios móviles de
orden 3 se presentan en la siguiente tabla:

Empleando Excel se muestra en la
siguiente figura:

2) El último valor del promedio
móvil, que en este ejemplo es 26,33, representa el
pronóstico de las ventas para el trimestre número
13, y teóricamente para todo trimestre futuro.

3) Para resolver lo planteado se toma en
cuenta las 3 últimas ventas con sus respectivos pesos o
ponderaciones. Estos datos se presentan en la siguiente
tabla:

Reemplazando valores en la fórmula
de la media aritmética ponderada se obtiene:

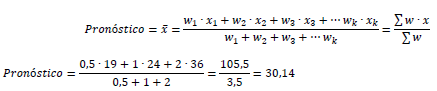
El valor 30,14 es el pronóstico de
ventas para el trimestre número 13.

Los cálculos en Excel se
muestran en la siguiente figura:

4) El gráfico en el que constan las ventas y los
promedios móviles se muestra en la siguiente figura
elaborado empleando Excel:

Empleando Graph se muestra en la siguiente
figura:

4.2) SUAVIZACIÓN EXPONENCIAL

Este método contiene un mecanismo de
autocorrección que ajusta los pronósticos en
dirección opuesta a los errores pasados. Es un caso
particular de promedios móviles ponderados de los valores
actuales y anteriores en el cual las ponderaciones disminuyen
exponencialmente. Se emplea tanto para suavizar como para
realizar pronósticos. Se emplea la siguiente
fórmula:

Donde:

yt+1= pronóstico para cualquier
período futuro.

a = constante de suavización, a la cual se le da
un valor entre 0 y 1.

Xt= valor real para el período de
tiempo.

Yt= pronóstico hecho previamente
para el período de tiempo

Cuando exista menos dispersión en los datos
reales respecto a los datos pronosticados entonces será
más confiable el método empleado. Para saber cuan
preciso es el método empleado en la realización del
pronóstico se utiliza la siguiente fórmula del
cuadrado medio del error (CME) como indicador de
precisión del pronóstico:

Siendo n el número de
errores

Ejemplo ilustrativo

Con los siguientes datos acerca de la
ventas en miles de dólares de la Empresa D & M durante
los últimos 12 meses:

1) Suavizar los datos empleando el método de
suavización exponencial con a = 5. Pronosticar las
ventas para el mes de septiembre. Calcular el cuadrado medio del
error. Elaborar un gráfico en el que consten las ventas y
los pronósticos.

2) Suavizar los datos empleando el método de los
promedios móviles de orden 3. Pronosticar las ventas para
mes de septiembre. Calcular el cuadrado medio del error. Elaborar
un gráfico en el que consten las ventas y los promedios
móviles.

3) ¿Qué método es el más
preciso?

Solución:

• 1) Realizando los cálculos se
  suavizamiento se obtienen los resultados respectivos de
  pronóstico, los cuales se presentan en la siguiente
  tabla:

Observando la tabla anterior se tiene que el
pronóstico de ventas para el mes de septiembre es de
6,798, o para cualquier período futuro, ya que los datos
no presentan una tendencia sino que se supone que varían o
fluctúan a largo plazo alrededor de este valor
promedio.

Calculando el cuadrado medio del error se obtienen los
siguientes resultados, los cuales se presentan en la siguiente
tabla:

Aplicando la fórmula se obtiene el
cuadrado medio del error:

Los cálculos realizados en Excel
se muestran en la siguiente figura:

La gráfica de las ventas y los
pronósticos con el método de suavización
exponencial elaborada en Excel se muestra en la siguiente
figura:

2) Suavizando los datos empleando el
método de los promedios móviles de orden 3
elaborado en Excel se muestra en la siguiente figura:

Observando el gráfico anterior se
tiene que el último pronóstico calculado es de 7,
por lo que el pronóstico para septiembre es de
7.

Observando el gráfico anterior se
tiene que el cuadrado medio del error es de 4,522.

La gráfica de las ventas y los
pronósticos con el método de los promedios
móviles elaborada en Graph se muestra en la siguiente
figura:

3) Como CME en el método de suavización
exponencial es de 7,09 y con el método de los promedios
móviles es de 4,52, se concluye que el método de
los promedios móviles es el más preciso para este
ejemplo ilustrativo.

EL PRESENTE TEXTO ES SOLO UNA SELECCION DEL TRABAJO
ORIGINAL.
PARA CONSULTAR LA MONOGRAFIA COMPLETA SELECCIONAR LA OPCION
DESCARGAR DEL MENU SUPERIOR.