Gráficas de control de la calidad para variables

Estas gráficas de control ayudan a la
detección de la variación de causa asignable
(variación en el producto o proceso de producción
que señala que el proceso está fuera de control y
que se requieren medidas correctivas)

La Gráfica
R

Mide la variación en el rango de las muestras.
Aunque la desviación estándar es una medida que
depende de la dispersión, las técnicas de control
de calidad generalmente confían en el rango como un
indicio de la variabilidad del proceso.

Límite superior de control para el
rango

LSCR=R+3sR

Límite inferior de control para el
rango

LICR=R-3sR

Donde sR es la desviación estándar en los
rangos muestrales. Sin embrago, en la práctica, es
más simple de utilizar

Límite superior de control para el
rango

LSCR=D4R

Límite inferior de control para el
rango

LICR=D3R

Los valores D4 y D3 se toman de la tabla de factores
críticos de las gráficas o cartas de control de
acuerdo al tamaño n de la muestra y el rango promedio de
los rangos muestrales R=SRk, siendo k = número de
muestras

La Gráfica
X

Se diseña para medir la variación en las
medias muestrales alrededor de algún nivel generalmente
aceptado.

Se tiene entonces:

Límite superior de control para las
medias

LSCX=X+A2R

Límite inferior de control para las
medias

LICX=X-A2R

Donde:

Siendo k = número de muestras

Ejemplo ilustrativo

Una fábrica elabora planchas de madera para tapas
de mesas, las cuales deben cumplir ciertas especificaciones de
tamaño. Para garantizar que se cumplan estos
estándares de calidad, se recolecta K= 24 muestras
(subgrupos) de tamaño n = 6, y mide su largo. Los
resultados aparecen en la siguiente tabla:

a) Calcular el rango promedio

b) Calcular el límite superior de control para el
rango

c) Calcular el límite inferior de control para el
rango

d) Elaborar la gráfica R.

e) Calcular X

f) Calcular el límite superior de control para
las medias

g) Calcular el límite inferior de control para
las medias

h) Elaborar la gráfica X.

Solución:

Calculando el rango se obtiene:

Recuerde que el rango es igual al valor mayor menes el
valor menor, es decir:

R=Xmáxima-Xminima

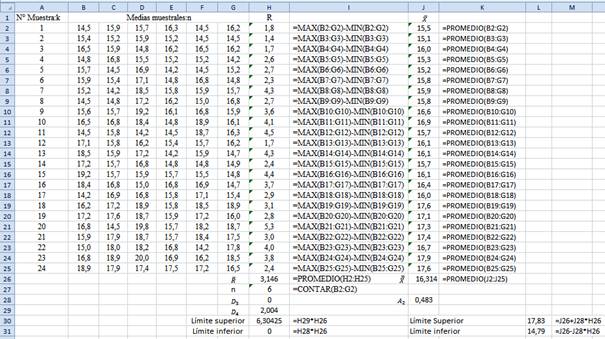
a) Calculando el rango promedio se tiene:

b) Calcular el límite superior de control para el
rango

Con lectura en la tabla para n = 6 se obtiene
D4=2,004

Calculando el límite superior se
obtiene:

LSCR=D4R=2,004·3,146=6,3

c) Calcular el límite inferior de control para el
rango

Con lectura en la tabla para n = 6 se obtiene
D3=0

Calculando el límite inferior se
obtiene:

LICR=D3R=0·3,146=0

d) Elaborando la gráfica R en Graph se
obtiene:

Interpretación: Observando la
gráfica se concluye que la misma está bajo control,
ya que no existen variaciones de causa asignable, es decir, no
existe ningún punto que se salga de los límites de
control.

e) Calculando x se obtiene:

Calculando X se obtiene:

f) Con lectura en la tabla para n = 6 se obtiene
A2=0,483

Calculando el límite superior se
obtiene:

LSCX=X+A2R=16,314+0,483·3,146=17,83

g) Calculando el límite inferior se
obtiene:

LICX=X-A2R=16,314-0,483·3,146=14,79

h) Elaborando la gráfica X en Excel se
obtiene:

Elaborando la gráfica X en Graph se
obtiene:

Interpretación: Observando la
gráfica se concluye que la misma está fuera de
control, ya que, la muestra 23 representa una variación de
causa asignable, es decir, la muestra 23 se sale del
límite superior de control.

Los cálculos en Excel se muestran en la siguiente
figura:

Tarea de
interaprendizaje

1) ¿Qué es variación de causa
asignable?

2) Realice un organizador gráfico de las
Gráficas para la Media

3) Realice un organizador gráfico de las
Gráficas para el Rango

4) Una fábrica produce estructuras para
computadores de mesa, los cuales deben cumplir ciertas
especificaciones de tamaño. Para garantizar que se cumplan
estos estándares de calidad, el gerente de la
fábrica, recolecta K= 24 muestras (subgrupos) de
tamaño n = 6, y mide su ancho. Los resultados aparecen en
la siguiente tabla

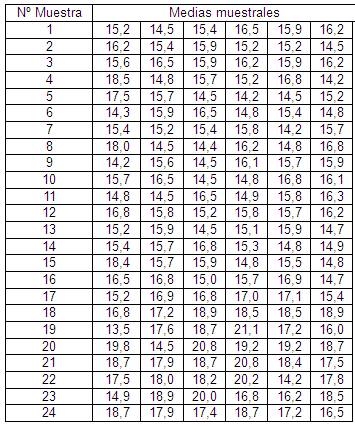
4.1) Calcular el rango promedio 2,9625

4.2) Calcular el límite superior de control para
el rango 5,936

4.3) Calcular el límite inferior de control para
el rango 0

4.4) Graficar manualmente la gráfica
R.

4.5) ¿El proceso está bajo control?.
¿Por qué?

5) Empleando los conocimientos de la gráfica R
plantee y resuelva dos problemas de aplicación, el uno
con

6) Empleando los datos de la fábrica que produce
estructuras para computadores de mesa, problema presentado
anteriormente.

6.1) Calcular X 16,3194

6.2) Calcular el límite superior de control para
las medias 17,75

6.3) Calcular el límite inferior de control para
las medias 14,89

6.4) Graficar manualmente la gráfica
X.

6.5) ¿El proceso está bajo control?.
¿Por qué?

6.6) Escriba una semejanza y una diferencia entre la
gráfica R del problema Nº 4 y la gráfica X del
presente problema.

7) Empleando los conocimientos de la gráfica X
plantee y resuelva dos problemas de aplicación, el uno
con

• Resuelva los problemas anteriores empleando el
  programa Excel (para los cálculos) y el programa Graph
  (para las gráficas).

Autor:

Mario Orlando Suárez
Ibujes