- Aparato
fonador - Formantes
- Reconocimiento del habla
empleando técnicas de comparación de
patrones - Estudio basado en la
posición de los formantes - Procesamiento de la voz
en el dominio del tiempo - Energía y
magnitud - Estimación
espectral por predicción lineal
(LPC) - Modelos de
señales - Procesos discretos de
Markov y Cadenas ocultas de Markov (HMM) - Redes neuronales
artificiales - Estructura de una red
neuronal artificial - Aprendizaje
- El
Perceptrón - Perceptrón
multicapa - Perceptrón
multicapa con capas de retardo - Entrenamiento de varias
capas - Método del
gradiente (aplicado a retropropagación) : ventajas y
limitaciones - Refuerzo de estos
conceptos - Sobreaprendizaje
(overfitting) o cómo las RNA pueden "pasarse de
listas" - Conclusiones
- Bibliografía
– Si nos paramos a pensar un poco sobre este tema,
descubriremos que la cantidad de información que se necesita para realizar
este trabajo es
demasiada, empezando por los modelos
básicos, el tema se bifurca en muchos caminos y es
prácticamente imposible obtener una visión completa
de todo. Debido a su complejidad matemática, física, informática y lingüística tendríamos que
hacer un estudio previo de todos estos campos, lo que requiere
mucho tiempo de
estudio.
Me he limitado a describir los procesos de
reconocimiento de voz de una manera superficial e intuitiva,
haciendo hincapié en uno de los métodos
más exitosos hasta ahora: Redes
Neuronales. Por tanto, iré de menor a mayor
dificultad.
Me ahorrare fórmulas matemáticas complejas ya que considero este
trabajo como una introducción teórica para luego
poder
profundizar, en alguna otra ocasión, en cualquiera de los
temas expuestos aquí. (Daré por sabido, conceptos
de muestreo y
demás.) Tocaré temas de probabilidad,
pero como he dicho antes, lo haré de forma teórica,
intuitiva y superficial. Considero ésta la mejor
propuesta, porque para saber de algo en concreto
habrá que empezar desde el principio; no habrá
ningún momento en que el lector se pierda, espero, por
tanto, aclarar el nivel de dificultad de este trabajo.
¿Qué es reconocimiento de voz?:
– Al hablar de reconocimiento de voz, podemos
imaginarnos varios campos de aplicación. Desde la domótica hasta la inteligencia
artificial.
¿Emplearemos reconocimiento de palabras aisladas
o del habla continua? ¿Será o no será
dependiente del locutor? ¿tendrá una gramática restringida?. Todo depende de la
aplicación que queramos. Por ejemplo, si queremos un
sistema que
reconozca un número limitado de palabras para poder apagar
o encender las luces de nuestra casa, está claro que
grabando unos cuantos ejemplos que servirán de patrones a
identificar con las entradas, bastará para poder
satisfacer nuestras necesidades.
Imaginemos que en vez de 10 palabras queremos tratar un
vocabulario completo y no sólo eso, queremos poder hablar
con naturalidad y que el sistema identifique las palabras, las
frases y el significado. Es decir, queremos que un robot nos
entienda, para ello el nivel de complejidad se eleva a un nivel
casi impensable.
Un sistema de reconocimiento de voz podrá operar
identificando:
- Palabras aisladas
- Fonemas (mayor complejidad)
Éste último podrá utilizarse para
reconocer palabras, frases, etc. Además de su
entendimiento.
Si nos interesa un sistema simple de reconocimiento de
palabras, actualmente se venden módulos que funcionan
mediante comparación de patrones. Necesitaremos almacenar
en una memoria dichos
patrones y luego se compararán las entradas con
éstos dando una salida de tipo binario (1 ó
0).
El método de
funcionamiento se podrá comprender más adelante, ya
que conociendo lo difícil se intuye lo fácil. Por
ello me voy a ceñir en el reconocimiento de fonemas, que
es actualmente el sistema más perseguido por los
más ambiciosos investigadores.
Como veremos, no se analiza fonema por fonema, sino que
se divide la señal (en función
del tiempo) en pequeñas ventanitas de unos 20 mseg. y se
van analizando las frecuencias además de sus
variaciones.
La dificultad empieza a nacer cuando nos damos cuenta de
que al pronunciar las palabras: "siete" y "nueve" hay cuatro
letras señaladas en negrita que parecen ser la misma, pero
lo mejor de todo es que la pronunciación, en al menos dos
de ellas ,es diferente, aunque sea la "e" depende mucho de
dónde la coloquemos, qué es lo que la precede y en
qué estado de
ánimo la pronunciamos. Es decir, necesitamos predecir de
alguna manera qué tipo de "e" es. Aquí entra en
juega la probabilidad, pero retornemos al principio explicando
todo paso por paso.
– Partiendo del conocimiento
de la producción de sonidos por las cuerdas
vocales, hay que tener en cuenta qué es lo que nos hace
distinguir las letras y las consonantes.
Si acudimos a referencias fonéticas, nos
explicarán que hay ciertas consonantes oclusivas, otras
son fricativas, etc. Y esto influye muchísimo en el
traspaso del dominio del
tiempo a la frecuencia.
Como ejemplo, citemos la "s", en un espectrograma
veríamos ruido a altas
frecuencias, sin embargo la "a" tiene ciertas componentes
frecuenciales de alta energía.
La posición de la lengua, la
abertura de la boca, los labios, todo un conjunto fonético
que consigue emitir infinidad de sonidos. En nuestro idioma se
acotan dichos sonidos para poder construir un lenguaje
ordenado.
Otros idiomas recogen otros sonidos producidos por el
aparato fonador que difieren bastante del castellano.
Si emitimos un sonido constante
y sólo movemos la lengua, nos daremos cuenta de que en
cierta manera producimos el mismo sonido pero cambiamos las
distribuciones armónicas… Los formantes.
– Son frecuencias que entran en resonancia en las
cavidades nasales y orales, saliendo hacia el exterior como la
información más importante del habla.
En reconocimiento de voz solemos anular la frecuencia
fundamental y nos quedamos con los dos primeros
formantes.
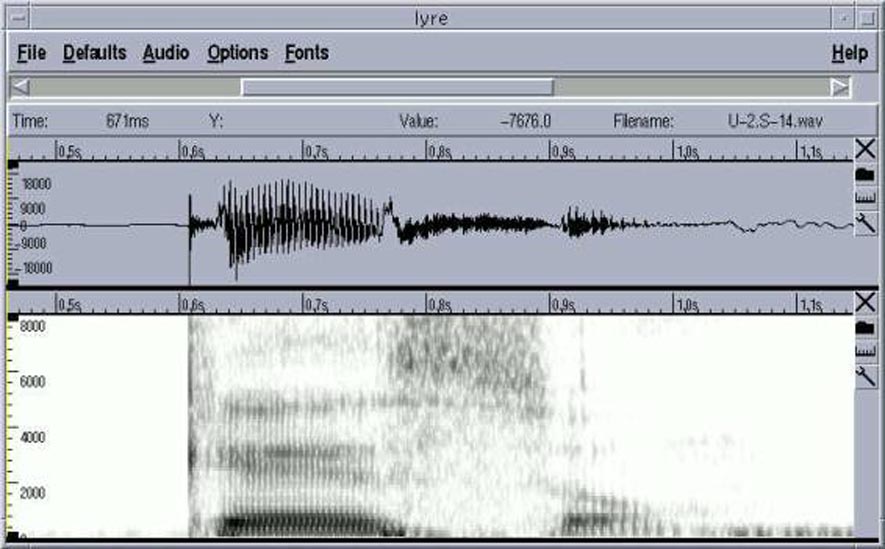
Éste es el ejemplo de la palabra "queso" se
visualiza perfectamente las altas frecuencias debidas a la "s" y
los dos primeros formantes de la "e", así como el tono
fundamental.
Y aquí está la primera bifurcación,
la fonética, la cual se merece un estudio bastante
detallado. Voy a suprimir debido al propósito de este
trabajo que he comentado en la introducción.

Ésta es la palabra "soy". Podemos ver
perfectamente que el primer formante se desplaza en frecuencia
por el efecto del corrimiento de la lengua en el fonema
/oi/.
Para hacerse una idea de lo grande que puede llegar a
ser este estudio fonético, comentaré que una de las
referencias que he usado, planteaban como pregunta en una de las
secciones: ¿Por qué alguien en su sano juicio se
dedicaría al análisis del lenguaje?…
Debemos pensar un poco en todo esto y hacernos muchas
preguntas acerca de las vocales y consonantes, y saber
además, que la diferencia entre una "a" y una "e" reside
en la ubicación de sus formantes. Nuestro cerebro analiza
esas frecuencias y su relación entre ambas, ante la duda,
suponemos…qué vocal puede ser. Eso lo podemos traducir
como una operación probabilística que realizan
nuestras neuronas concluyendo a una decisión
final.
Reconocimiento del habla
empleando técnicas
de comparación de patrones:

– Su principal ventaja inmediata reside en que no es
necesario descubrir características espectrales de la voz
a nivel fonético, lo que evita desarrollar etapas
complejas de detección de formantes, de rasgos distintivos
de los sonidos, tono de voz, etc.
Esto está muy bien para un número finito
de palabras, cuyo número no sea muy grande. Si queremos
implementar esto para un completo entendimiento de nuestro
lenguaje, a ver quien se atreve a coger un diccionario y
grabar palabra por palabra. Sería una auténtica
locura, además de ser inútil porque si por ejemplo
pronunciásemos la palabra "queso" tendríamos que
hacerlo exactamente igual que en la grabación.
Tendríamos que decir "queso" con la misma velocidad, con
el mismo tono…etc. Si nuestro "queso" se pronuncia muy
rápido, habría que ajustar los tiempos de inicio y
de final, pero si el sistema no está seguro de que sea
esa palabra…adiós muy buenas. Necesitaríamos un
sistema que aprenda por sí mismo éstas posibles
deficiencias y se atreva a estipular qué palabra
es.

La base de datos
que necesitaríamos sería tan grande, que
haría falta sistemas toscos
de almacenamiento.
Cuando el sistema intente buscar la palabra, al menos
basará su funcionamiento en el establecimiento de una
distancia matemática entre vectores, de
tal manera que se puede calcular lo cercano que se encuentra cada
patrón.
De todos modos, existe la necesidad de aplicar este
sistema única y exclusivamente a ciertos casos donde el
número de palabras necesarias sea
pequeño.
También se puede constituir los grupos de
patrones por unidades tales como sonidos básicos (fonemas
y demás clasificaciones de sonidos cortos).
Al grabar estos sonidos en la base de datos, se
obtendrán sus características espectrales (suele
hacerse con los parámetros LPC, de los cuales hablaremos
después).
Por último mencionar que por mucho que se mejore
éste sistema, siempre existirá el error al
normalizar en tiempo y amplitud éstas señales
de entrada para que coincidan con el patrón.
Estudio basado en la
posición de los formantes:
– Para obtener una información detallada de los
tres primeros formantes hay que recurrir a otra solución.
Un simple espectrograma nos da información…pero no
tanta. ¿Qué podríamos hacer para poder
diferenciar unas personas de otras?, ¿qué
haríamos para poder ver las relaciones entre formantes de
una manera más precisa?. La solución está en
construir gráficas donde F1 (primer formante) se
situé, por ejemplo, en el eje de abscisas, F2 en el eje de
ordenadas, y así probando todas las combinaciones.
También podemos establecer gráficos de 3 dimensiones donde intervienen
los tres formantes.

Esta gráfica muestra lo dicho.
Cada color representa
una persona
diferente, si nos fijamos en la de arriba a la derecha (F2 eje x,
F1 eje y), podremos observar las vocales (i,e,a,o,u) de derecha a
izquierda.
Cuanto más a la derecha esté la
información, mayor frecuencia tendrá F2.
Cuanto más arriba, menor frecuencia tendrá
F1.
Las demás gráficas se usan para
complementar casi siempre a la que hacemos referencia. De esta
forma podremos distinguir entre quién habla y qué
sonido produce dicha persona.
Pero una aplicación recóndita reside
aquí. ¡Podemos diferenciar si una vocal es adyacente
a una consonante bilabial (por ejemplo, la "b"), o si la misma
vocal es adyacente a una consonante velar, o a una
dental/interdental… Lo que quiero expresar con esto es la
solución a la identificación de las consonantes
adyacentes a una misma vocal. Bien antes hemos dicho que una
misma vocal puede pronunciarse de diferentes maneras según
sus consonantes adyacentes.
En éstas gráficas podríamos
apreciar cómo F1 y F2 bajan en frecuencia (desplazadas
hacia la izquierda y hacia arriba) en el caso de tener adyacente
una consonante bilabial.
F1 baja y F2 sube en el caso de tener una consonante
velar, este caso se ve claramente porque es la parte coloreada de
azul en la gráfica de arriba a la derecha, donde podemos
observar que está desplazada de las demás hacia
arriba y hacia la derecha (F1 baja y F2 sube).
Un análisis mucho más profundo
revelaría grandes detecciones sobre la evolución de los formantes, pero no
entraremos en detalle porque podemos perdernos todos juntos,
tanto yo como el lector.
Procesamiento de la voz en el
dominio del tiempo:
– Debido a la naturaleza
cambiante de la voz, resulta más conveniente aplicar el
análisis a porciones de voz, ya que nuestro interés es
observar la evolución de los distintos parámetros
calculados; por ello se procesan porciones o ventanas de la
señal.
Si nos damos cuenta, nos vamos alejando poco a poco de
la comparación brusca de palabras o fonemas. Estamos
llegando a un nivel superior donde el descubrimiento de la
evolución de los formantes nos obliga a tratar la
señal con porciones de unos 20 mseg. como dijimos
anteriormente.

Pero esto no es todo, cada ventanita tendrá
asociada un peso, es decir, no todas las secciones tendrán
mayor importancia. De esta forma las muestras quedan ponderadas
con los valores de
la función escogida. En este ejemplo, (Hamming) las
muestras que se encuentran en los extremos de la ventana tienen
un peso mucho menor que las que se hallan en el medio, lo cual es
muy adecuado para evitar que las características de los
extremos del bloque varíen la interpretación de lo que ocurre en la parte
más significativa (central) de las muestras
seleccionadas.
Existe un pequeño solapamiento en los extremos de
las ventanas, ¿por qué?, pues para proporcionar una
mejor calidad en los
resultados obtenidos ya que los valores (de la
ventana) en sus extremos, quedan muy reducidos.
Pero como siempre pasa, en toda ley donde algo
mejora, otra… empeora; en este caso va a repercutir en los
tiempos de respuesta de los algoritmos
utilizados, alargándolos ligeramente.
Hay varios tipos de ventanas: Ventana rectangular,
ventana Hanning, ventana Hamming… quizá esta
última es la más utilizada.
Para cualquier ventana, su duración determina la
cantidad de cambios que se podrán obtener. Con una
duración temporal larga, se omiten los cambios locales
producidos en la señal, mientras que con una
duración demasiado corta, se reflejan demasiado los
cambios puntuales y se reduce la resolución
espectral.
– Tanto la energía como la magnitud son
útiles para distinguir segmentos sordos y sonoros en la
señal de voz.
Existen otras maneras para identificar consonantes, hay
un método denominado "cruces por cero y máximos"
donde por ejemplo la "s" provoca que las muestras consecutivas de
esa consonante difieren de signo (señales discretas).
Generalizando más, podremos decir que una señal
clasificada como ruido (la "s" es un ruido de alta frecuencia)
provoca en la amplitud un cambio de
signo. De esta manera se pueden localizar consonantes
fricativas.
También se encuentran los bancos de
filtros, usados para calcular la energía de la
señal en cada ventana, y así poder representar un
espectro.
Estimación espectral
por predicción lineal (LPC):
– Su importancia es mayor que la que su propio nombre
sugiere. Es una de las técnicas más usadas en el
procesamiento de señales de voz.
Esta técnica ha probado ser muy eficiente debido
a la posibilidad de parametrizar la señal con un
número pequeño de patrones con los cuales es
posible reconstruirla adecuadamente. Estos parámetros van
cambiando poco a poco en función de la señal en el
tiempo Otra ventaja es que no necesita demasiado tiempo de
procesamiento.
El modelo
matemático sugiere que el tracto vocal puede modelarse
mediante un filtro digital, siendo los parámetros los que
determinan la función de transferencia.
Esto consiste en que, dado un segmento de palabra, se
extraen sus parámetros que en este caso vienen a ser los
coeficientes del filtro.
El sistema LPC es sin duda una manera acertada de poder
registrar una señal, ya que, en vez de registrar dicha
señal, se transforma todo en un filtro con determinados
coeficientes, de manera que al reconstruir la señal, se le
"inyecta" un tren de pulsos periódicos o una fuente de
ruido aleatorio que al pasar por el filtro se transformará
en la señal original, es decir, en nuestra señal de
voz.
- El tren de impulsos producirá señales
sonoras q La fuente de ruido aleatorio producirá
señales no sonoras. - De esta manera, el filtro viene a representar un
modelo del tracto bocal.
Si aplicásemos en vez de este sistema la
transformada discreta de Fourier, se podría observar que
coinciden en las resonancias que vienen a ser las que
caracterizan el contenido frecuencial de la señal vocal,
pero el espectro de la señal tratada por el sistema LPC se
caracterizaría por tener contornos más suaves de lo
normal, se podría decir que "suaviza" el
espectro.
Aquí vendría otra bifurcación, en
este caso matemática, ya que para la obtención de
las ecuaciones del
filtro, hay un largo recorrido de algoritmos, convoluciones, etc.
Por tanto no pondré ninguna fórmula.
Hasta ahora, hemos visto los principios
básicos, pero quedan muchas cosas que dar. En este punto
es donde cabe mencionar los sistemas avanzados como son las
cadenas ocultas de Markov (HMM) y las redes neuronales. Por
supuesto debe haber más métodos, (como los
algoritmos genéticos), pero valoro estos dos como los
más importantes.
– Los modelos de señales que existen para
caracterizar señales, pueden clasificarse de modo general
en determinísticos y estocásticos (o
de señales aleatorias). Esta clasificación se basa
en la naturaleza de la señal tratada.
Los modelos determinísticos utilizan propiedades
conocidas de la señal, y así poder estimarla de
forma inmediata. Ejemplo: Onda senoidal, la cual puede
caracterizarse por Amplitud, Fase y Frecuencia.
Por otra parte, los modelos estocásticos estiman
propiedades estadísticas de las señales. (series
de Gauss, series de Poisson, etc). Se asume que la señal
modelada puede caracterizarse como una serie paramétrica
aleatoria, y los parámetros de la serie aleatoria pueden
estimarse de manera definida y precisa. Por esto los modelos
estocásticos son una aproximación particularmente
adecuada para el reconocimiento de voz.
El modelo estocástico más popular empleado
en el reconocimiento de voz es el HMM
Procesos discretos de Markov
y Cadenas ocultas de Markov (HMM):
– Los HMMs se han utilizado en diversas aplicaciones
como sistemas de comunicación, biología molecular
(para el análisis de las secuencias de ácidos
proteicos y nucléicos), etc.
A este modelo se le llama "oculto" (hidden), en
el sentido en que la secuencia de estados que producen una
secuencia de patrones determinada, no puede ser
observada/determinada.
Dependiendo de cómo evolucionen los estados,
podemos hablar de HMMs ergódicos (cualquier estado se
puede alcanzar desde cualquier otro estado) o HMMs left-to-right
(donde el modelo únicamente lleva a cabo transiciones
hacia delante).
Una característica importante es que estos
sistemas tienen un futuro independiente del pasado, lo cual no
ocurre en Redes Neuronales.
Estos modelos que acabo de describir serían la
cuarta bifurcación, ya que se necesita una amplia gama de
conocimientos estadísticos para poder llegar a comprender
esto.
Por falta de conocimientos estadísticos no puedo
decir más sobre las HMMs.
Está claro que para el reconocimiento de voz
necesitamos sistemas estadísticos como el de Markov, pero
la aplicación de Redes Neuronales va a superar con creces
cualquier modelo estadístico que se le enfrente. Por
supuesto, hay fallos en las Redes Neuronales, pero son el
último avance en cuanto a este tema.
Dedicaré el resto del trabajo a explicar
exclusivamente las Redes Neuronales ya que por lo menos, se puede
profundizar un poco en ellas, sin necesidad de ser un genio de
estadística ni de matemática. Es
obvio que las siguientes explicaciones sigan siendo
superficiales, porque a ver quien me enseña a programar
una red de ese
calibre, necesitaría una asignatura dedicada
exclusivamente a ello.
He hecho todo lo posible por explicarlo de manera
filosófica-científica con el fin de que se llegue a
comprender, por lo menos, algo. Y así introducirnos y
culturizarnos un poquito de lo que pasa a nuestro
alrededor…
– Se puede definir como: "Una nueva forma de computación inspirada en modelos
biológicos".
Por ello, vamos a ver primero el modelo
biológico:

Una neurona se
compone de dendritas(entradas),cuerpo(decisión) y
axón(salida).
Por supuesto, el funcionamiento de una neurona es
muchísimo más complejo de lo que aparentemente
parece. La información en sí, es el potencial
eléctrico.
En nuestro cerebro tenemos miles de neuronas
interconectadas entre sí, lo que equivale a unas 10E15
conexiones (aproximadamente).
El modelo que vamos a tomar de ella es el
siguiente:

Los sistemas neuronales biológicos presentan un
mecanismo de vital importancia para controlar el flujo de la
información que transita a través de las neuronas.
Para ello están los neurotransmisores, que actúan
químicamente sobre la sinapsis, amplificando o
disminuyendo la cantidad de potencial que se transmite de una
neurona a otra. Nosotros modelaremos un neurotransmisor como una
multiplicación de la salida por un peso
(número).
Éste hará las veces de
neurotransmisor.
Por tanto, una red neuronal aplicada a
cualquier sistema de reconocimiento, se basará simplemente
en modelos matemáticos calculados con un lenguaje de
programación.
Actualmente, se usa para varias aplicaciones
además de la de reconocimiento de voz. Por ejemplo: Para
la identificación de señales ultrasónicas en
la emisión acústica, para detectar posibles grietas
en los tanques de las petrolíferas. En este campo,
interesa saber cómo se agrietan los tanques cuando son
sometidos a una tensión, ya que hay varios tipos de
ruptura, algunas son poco importantes y otras lo son mucho. Por
tanto, conviene un sistema que analice automáticamente
todas las señales y haga un informe del
resultado. Actualmente, estos sistemas avanzados no existen en
España
debido a que las petrolíferas no quieren gastar dinero en
esto, en cambio en Francia, USA,
etc. Hay una gran competitividad
en este sector.
Volviendo a nuestra aplicación de reconocimiento
de voz, en la siguiente figura podremos ver más
detalladamente las entradas (u), la salida (y) y los pesos
(w).

Si W>0 ® sinapsis excitadora
Si W=0 ® no existe conexión
Si W<0 ® sinapsis inhibidora
Hay que dejar bien claro que las entradas no van a ser
coeficientes LPC ni nada por el estilo. Simplemente, por ejemplo,
serán los parámetros de una Transformada de
Fourier.
Cuando multiplicamos la entrada por el peso (u*w)
tendremos un valor con el
cual decidiremos si a la salida daremos un 1 o un 0.
Existe un umbral q tal que si (u*w-q) es mayor que cero, la salida vale y =
1.
A primera vista, podemos pensar que la salida
será un impulso tipo escalón, pero esto no es
así ya que necesitamos una función derivable (por
motivos de programación) así que aproxima esa
señal a una de tipo sigmoidea (continua y
derivable).
Estructura de una red
neuronal artificial:
– Una vez establecido el comportamiento
de una neurona artificial, vamos a conectar neuronas entre
sí con el fin de formar una red de
computación.

– Así como las neuronas biológicas
están continuamente creando y destruyendo conexiones,
nosotros vamos a regular esta función mediante la
variación del valor de los pesos. En términos
básicos podemos entender esto como: Llega la entrada, se
multiplica por el peso, lo cual implica una salida de tipo 1
ó 0. Cómo esto no es una función exacta y
debido a que cuando tenemos muchas neuronas es
prácticamente imposible predecir el valor de los pesos
para que el sistema funcione maravillosamente bien, entonces se
establecen unos valores de los pesos de manera aleatoria. Si el
resultado no es bueno, se le comunica de alguna forma para que
aumente o disminuya el valor del peso. Y así, tenemos un
sistema que aprende por sí solo.
Hay muchos tipos de aprendizaje, ya
que se necesitan probar muchos algoritmos para ver cuál
funciona mejor. Por la década de los 70, nació el
sistema de retropropagación (Algoritmo Back
Propagation), en el que cuando la última capa de salida
suelta un valor, comienza el proceso
contrario (propagación hacia atrás) analizando
qué es lo que ha pasado en cada neurona de cada capa y
dando órdenes a cada una de ellas para ver cómo
puede mejorar. Podemos asimilar esto como una especie de programa llamado
"maestro" que supervisa el trabajo de
sus alumnos.
Este sistema revolucionó el mundo del aprendizaje
en redes neuronales y hablaremos más profundamente de esto
más adelante.
Si nos sumergimos un poco más en el sector del
aprendizaje, podemos definir uno de los muchos algoritmos que
existen.
Por ejemplo, aprendizaje supervisado por
corrección de error, aquí se opera de la manera
siguiente:
Esperamos un valor a la salida, pero obtenemos uno
distinto. Entonces dichos valores se restan y la diferencia se
aplica a un factor que regula la velocidad de aprendizaje.
Así, cuanto más cerca estemos de nuestra
solución, el sistema irá con más cuidado.
Todo ello se engloba en un incremento del peso. En otras
palabras:
DW
= a*Y*(d-Y) (Regla
delta)
d: valor de salida deseado
a: factor de
aprendizaje (regula la velocidad de aprendizaje)
DW
= Wactual – Wanterior : modificación del peso
W.
d-Y: error que se produce en la
neurona.
A este tipo de aprendizaje, se le denomina Hebbiano,
dada una suposición de Hebb en 1949.
Vamos a definir un tipo de red neuronal, profundizaremos
sobre él, pero hay que tener en cuenta que existen otros
casos mucho más complejos, los cuales, parten de la idea
básica de éste:
– Presenta una sola neurona de cómputo, de
ahí su sencillez. Es un tipo de estructura mostrada
a continuación:

Las neuronas de menor tamaño pertenecen a la capa
de entrada y son parte del formalismo de la red. Se encargan de
recibir y distribuirlos datos del exterior, sin realizar
cómputos sobre los mismos.
En el caso más simple (N=2):
Y = f
[(X1*W1+X2*W2)-q]
Esto significa que el resultado de la neurona va a tomar
uno de los dos valores previstos en la función
escalón (-1 y 1). El valor de la salida dependerá
de si X1*W1+X2*W2 es mayor o menor que el umbral
q.
Por tanto podemos establecer la siguiente
ecuación
X1*W1+X2*W2-q = 0
Esta ecuación se corresponde con una recta que
separa un plano de 2 dimensiones en 2 partes, el valor de los
pesos y el del umbral, variará la posición de esa
recta en el plano.

Imaginemos ahora que N=3 . Eso implica una neurona
más en la capa de entrada, más exactitud de
computación y un plano de 3 dimensiones donde la
región que separa 1 de –1 es un plano. Cuando
tenemos por ejemplo 6 neuronas en la capa de entrada,
¿Podemos imaginarnos un espacio de 6 dimensiones?
Lógicamente no, pero matemáticamente
existe…
El método de aprendizaje que utiliza el
perceptrón es el supervisado por corrección de
error (Hebbiano).

Consiste básicamente en poner varias capas
elementales, como las anteriormente descritas, interconectadas
sucesivamente con el objeto de dotar a la red de la complejidad
suficiente para realizar la tarea requerida.
La función XOR se puede implementar con 3 capas
(al ser más compleja). Las funciones AND y
OR requieren una sola capa; cuando necesitemos operaciones de
cierta dificultad, tendremos que recurrir a tantas capas como
exija nuestro proceso.
Perceptrón multicapa
con capas de retardo:
Es el modelo más complejo. Consiste en la
inclusión de bloques (o capas) de neuronas que toman como
entradas las salidas de otro/s bloque/s en el instante anterior.
Esto permite que la red sea un sistema con memoria a corto plazo
(o en fase operativa). Esta memoria es muy diferente a la memoria
debida al entrenamiento que
presenta el sistema global (que podría llamarse memoria a
largo plazo o memoria en fase de entrenamiento).
Teniendo en cuenta que los patrones que pasamos a la red
varían con el tiempo se puede comprender la importancia de
estos retardos. Si la red no presenta retardos y la entrenamos
mediante unos parámetros variables con
el tiempo, impedimos que la red tenga en cuenta el orden en que
llegan los parámetros (no podría distinguir "uno"
de "onu" por ejemplo;
la red pudiera ser entrenada para distinguir unos ejemplos pero
sería imposible que generalizara).

Entrenamiento de varias
capas:
Cuando tenemos varias capas ya no tenemos un sistema de
ecuaciones lineales porque no hemos aplicado sólo una no
linealidad sino que hemos aplicado una no linealidad a una
aplicación lineal de varias no linealidades y esto ya no
se puede resolver como un sistema de ecuaciones lineales. Al no
tener una solución directa podemos pensar en buscar llegar
a la solución siguiendo varios pasos a partir de un punto.
El método de entrenamiento será por tanto
iterativo. Ahora se puede hablar más propiamente de
entrenamiento (mejora por fases).
Ahora lo que buscamos son dos cosas:
- Un punto de comienzo (pesos iniciales). Se
suelen escoger unos números aleatorios pero
pequeños. - Un camino. (o una dirección a seguir en cada paso). Lo que
nos interesa ahora es buscar en cada paso (cada
iteración) una dirección de nuestro espacio de
pesos que nos conduzca por un camino que lleve al objetivo: la
minimización del error.
Wn+1 = Wn +
DWn
La inteligencia
artificial pretende acercar el comportamiento de las máquinas
al comportamiento
humano. Esto pretende liberar al hombre de
tediosas tareas que hasta ahora sólo él
podía realizar. Para que la supuesta máquina pueda
conocer las necesidades del hombre es necesario que tenga una
forma (lo mejor posible) de comunicarse con él. Entre las
formas de comunicación creo que la voz juega un papel
primordial y es muy importante que se realice en ambos sentidos.
Si bien se puede pensar que las máquinas podrían
aprender por sí solas a entender la voz, quizá sea
más conveniente ayudarles mediante la creación de
reconocedores y sintetizadores de voz.
Intentaremos usar las Redes neuronales artificiales
(RNA) de manera eficiente para el reconocimiento de
voz. Para ello debemos elegir las entradas de nuestra red,
las salidas y la estructura
necesaria para que produzca las salidas deseadas (dadas unas
entradas). Después habrá que elegir un algoritmo de
entrenamiento y unos parámetros para después
realizarlo.
Método del gradiente
(aplicado a retropropagación) : ventajas y
limitaciones:
La ventaja de este método es que te da una
dirección para poder seguir un camino que puede minimizar
el error.
Recordando el concepto de
gradiente de una función escalar donde en este caso la
función escalar es el error y nuestro espacio vectorial es
el espacio de todos los pesos (cada uno de los pesos es una
dimensión del espacio):
El gradiente del error respecto a un vector
(pesos) es un vector cuya dirección es la
dirección de máximo crecimiento del error, su
módulo es la variación del error en esa
dirección (la de máxima variación) y su
sentido es el que indica el crecimiento.
ÑE = (dE/dw1, dE/dw2, …, dE/dwi, …, dE/dwm) = grad (E)
Como lo que nos interesa es minimizar el error lo que
debemos hacer es ir en sentido contrario al que indique el vector
gradiente (máximo decrecimiento).
– ¿ Cuánto debemos avanzar cada vez (cada
iteración) en esa dirección (que indica el
gradiente) para acercarnos convenientemente al
mínimo?.
Superficie de error para un solo
perceptrón

Como en principio no sabemos cuánto avanzar
podíamos pensar en una primera aproximación sumar
al vector de pesos el vector gradiente tal cual. Sin embargo,
hacerlo así podría llevarnos a dar saltos demasiado
grandes en esa dirección (y puede que lleguemos a otra
zona del espacio donde no hayamos mejorado). Para controlar esto
podemos multiplicar ese vector de gradiente por una constante
(que controlase el tamaño del salto en cada
iteración). Esta constante se suele llamar tasa de
aprendizaje (o tasa de entrenamiento "a") y esta forma
de actuar es la implementación básica del
método del gradiente del error.
El objetivo de este apartado es vincular todas las ideas
que se han mostrado, llegando por fin a la visión global
que nos permite "intuir" como funciona esto.
Observemos la siguiente figura:

Uno de los ejes es el error, el otro son los
pesos.
La gráfica representa la superficie de error
correspondiente a un modelo multicapa, ya que si miramos la
gráfica anterior, podemos observar los simple que resulta
para un solo perceptrón. A medida que vamos aumentando
capas, la superficie del error se vuelve más compleja.
Entonces aparecen los mínimos globales y los
mínimos locales.
- Los mínimos locales son todos aquellos
mínimos que están por encima de un mínimo
global. - El mínimo global es único y es el que
representa el menor de los errores.
El símbolo que aparece en la gráfica (con
la flecha) representa el avance de gradiente negativo que nos
acerca a un mínimo. ¡OJO! El sistema no sabe que
tipo de mínimo puede ser. Es decir, nosotros colocamos a
nuestro símbolo en alguna parte de la gráfica, y
él mismo decide ir bajando por el valle del error. La
colocación de dicho símbolo en una u otra parte del
valle viene determinada por la asignación inicial de los
pesos.
En otras palabras, cada punto en la superficie del error
corresponde a un conjunto de valores de los pesos de la red. Con
el gradiente descendiente, siempre que se realiza un cambio en
los pesos, se asegura el descenso por la superficie del error.
Así, el algoritmo sólo encuentra el valle
más cercano, lo que puede hacer que caiga en un
mínimo local. Sin embargo, ha de tenerse en cuenta que no
tiene por qué alcanzarse el mínimo global de la
superficie del error, sino que puede bastar con un error
mínimo preestablecido.
En el caso de la figura, nos encontramos en un
mínimo local, y el sistema converge hacia él. No
podremos salir de éste a menos que saltemos
bruscamente…

Problema: ¿ Cómo de grande debe ser ese
salto ? Posible solución: Empezar pegando saltos
pequeños y si vemos que "no salimos del agujero" (pozo de
potencial) probamos a ir dando saltos más
grandes.
El planteamiento sería similar a una pulga
patinadora miope ("rompetechos") que quiere bajar por una
montaña hacia una altura determinada lo más pronto
posible. Como conoce el entorno local (es miope pero no ciega)
bajaría por donde existiese la máxima pendiente
(gradiente) mirando a cada paso (de longitud la constante de
entrenamiento) para modificar el rumbo. Cuando no descendiera
más por sí sola (mínimo local)
miraría si llegó suficientemente bajo (tiene un
altímetro) y si no pegaría un salto para salir de
ese hoyo donde ha caído y buscar por otro
sitio.
Tenemos dos opciones:
1.Saltar de manera que los pesos se alejen de su valor
inicial cada vez más rápidamente (de
pequeños saltos, a saltos mayores) hasta que en uno de
esos saltos nos sitúen en otro valle. (Iremos
aumentando a
poco a poco, de manera que la magnitud de los saltos sea
cada vez mayor)(mirar gráfica de arriba).
a
es la velocidad de variación de los pesos
W
2.Teletransportarnos a otro remoto lugar de la inmensa
cadena montañosa. Es decir, cambiar drástica y
aleatoriamente los pesos, ya que puede haber grandes zonas
cuyos mínimos locales conllevan demasiado
error.
Cuando lleguemos a una zona donde el error sea
aceptable, entonces paramos, y evitamos el sobreaprendizaje
(sobreentrenamiento).
Sobreaprendizaje
(overfitting) o cómo las RNA pueden "pasarse de
listas":
Si la estructura de la red está sobredimensionada
y además el entrenamiento es demasiado largo puede que la
red se aprenda los ejemplos y disminuya demasiado su capacidad de
generalización Métodos para mejorar la
generalización:
– Añadiendo un ruido de unas
características determinadas a las entradas para
que no aprenda a distinguir un punto de otros sino que aprenda a
distinguir un conjunto de puntos cercanos de otro grupo de
puntos cercanos. Este concepto es muy importante, podemos pensar
que el sobreaprendizaje consiste en que el sistema llega a
reconocer a la perfección todas las características
de cada sonido, lo cual es erróneo ya que no es una
ciencia
cierta. Si nuestro cerebro funcionase así, nos
sería imposible reconocer el habla de las personas que
hablan con cierta gangosidad.
También podemos poner el caso extremo de una
persona que habla con la boca llena, en estos casos, nuestro
cerebro entiende la mayoría de las palabras por pura
probabilidad. Si todo esto lo trasladamos a una RNA (Red Neuronal
artificial) podemos intuir lo que pasaría si el sistema se
pasase de listo…
Volviendo al añadido de ruido, hay programas como el
WinNN que hacen esto automáticamente.
Los parámetros a ajustar en ese ruido
serían:
* función densidad de
probabilidad: Normalmente de tipo gaussiana.
* varianza:.
– Eligiendo una buena estructura: Si la red tiene
unas dimensiones justas (ni muy grandes ni muy pequeñas)
la red será capaz de funcionar sin que ocurra
sobreaprendizaje.
– Realizando un buen entrenamiento:
Eligiendo una buena condición de
finalización (disminuimos el error máximo que
se considera aceptable) no pararemos demasiado tarde, y de esta
manera, es más difícil que ocurra el
sobreaprendizaje.
Métodos para mejorar la generalización:
Pruning, Weight Sharing, Complexity Regularization.
Un buen método es dividir los datos en dos
conjuntos: uno
para el entrenamiento y otro para evaluar la
generalización.
– Hemos visto que una vez creada la red, hay que
entrenarla y permitirle que llegue a generalizar (sin
sobreaprendizaje).
El método de entrenamiento no es tan abstracto
como parece. Simplemente estableceríamos una primera
ecuación (supongamos que tenemos una sola capa y queremos
entrenar el aprendizaje de
una operación AND), en ésta ecuación
general:
Y = F[X1*W1 + X2*W2 +
q] = 0 ó
1
sustituiríamos las entradas por sus valores,
multiplicamos por los pesos, y si el resultado de Y, por ejemplo
(0*1 es 1, cuando tendría que ser 0), al no estar de
acuerdo aplicamos:
Error = (Salida deseada – Salida obtenida) =
0,1 ó –1
Si el valor de Y es 0 significa salida esperada. Con
cualquier otro valor (1,-1) salida errónea.
El proceso acabará cuando el error sea nulo,
durante una vuelta completa en los valores de entrada, si no es
asó seguimos operando.
Asignamos valores iniciales cuales sea: W1=2.2 ;
W2=1.2 ; q =-0.2
Según un aprendizaje Hebbiano donde:
W1 (t+1) = W1(t) + X1*Error
W2 (t+1) = W2(t) + X2*Error
q (t+1) =
q (t) +
X1ó2*Error
Sustituiremos las entradas en la ecuación de
salida en el siguiente orden:
00,01,10,11,00,01,10, etc.
Partimos de ciertos valores, comprobamos la salida, si
ésta es errónea nos iremos a calcular los nuevos
pesos y el nuevo error (donde X1ò2 se refiere que podemos
usar tanto uno como otro en cualquier ocasión), y con ello
volvemos a empezar.
Como la entrada X es también binaria, las
variaciones del peso serán de uno. Entonces con el nuevo
valor del peso calculamos en la ecuación los valores y le
metemos las nuevas entradas, y si sigue sin darnos el resultado
que queremos, volvemos ha hacer esto, una y otra vez…
Está demostrado que al final el sistema aprende
cómo realizar una operación AND ya que sólo
hay una capa, sólo hay un mínimo hacia el cual
convergeremos.
NOTA:
Si un resultado es aceptado Error = 0 y por mucho que
multipliquemos y sumemos en las tres ecuaciones, nada
cambiará.
Claro que éste es el caso más
sencillo…
También suelen representarse todas estas
ecuaciones de manera geométrica, y así poder ver el
proceso de aprendizaje mediante el plano XY y la(s) recta(s)
contenidos en él.
Y así acaba este pequeño temario, de nivel
básico. Ya que, si nos quisiésemos poner a
programar una red neuronal… no sabríamos por donde
empezar, pero al menos ahora tenemos una visión general de
qué es el reconocimiento de voz, cuales son sus posibles
aplicaciones, y lo más importante: Cuál es el
camino por el que se están debatiendo los
investigadores…Redes Neuronales Artificiales.
Uno de los conceptos que me ha gustado mucho dejar bien
claro, ha sido el de Inteligencia artificial, ya que se ha
demostrado cómo un sistema aprende por sí
solo.
Después de haber visto todos estos conceptos,
supongo que estaremos más convencidos de que la humanidad
no está tan lejos de fabricar un robot que entienda
perfectamente al ser humano, si por cada cosa que no
entienda, la gestiona y con ello aprenda…
La mayoría de la información encontrada
aquí, así como de las gráficas, dibujos y
espectrogramas, han sido extraídas de:
Libro: Reconocimiento de Voz y Fonética
Acústica. Autores: Jesús Bernal Bermúdez,
Jesús Bobadilla Sancho, Pedro Gómez Vilda.
Editorial: Ra-Maâ
http://www.intersaint.org/acid/
(Sección trabajos – Link MLP)
http://mailweb.udlap.mx/~sistemas/tlatoa/courses/syllabus.html
Christian Herrera
Extraído de http://www.adictosaltrabajo.com