Reseña
histórica
Abrahan De Moivre (1733) fue el primero en obtener la
ecuación matemática de la curva normal. Kart
Friedrich Gauss y Márquez De Laplece (principios del siglo
diecinueve) desarrollaron más ampliamente los conceptos de
la curva. La curva normal también es llamada curva de
error, curva de campana, curva de Gauss, distribución
gaussiana o curva de De Moivre.
Su altura máxima se encuentra en la media
aritmética, es decir su ordenada máxima corresponde
a una abscisa igual a la media aritmética. La
asimetría de la curva normal es nula y por su grado de
apuntamiento o curtosis se clasifica en
mesocúrtica.
Ecuación
Su ecuación matemática de la
función de densidad es:

Para calcular Y en Excel se procede de la siguiente
manera:
a) Se ubica valores para X del -3 hasta el 3. Se
insertar la función DISTR.NORM.ESTAND.N. En la ventana de
argumentos de función, en Z se seleccionada A2 que
representa al -3, y en Acumulado es escribe FALSO. Clic en
Aceptar. Se arrastra con el mouse para obtener los demás
valores.

b) Para obtener la gráfica se inserta
gráfico de dispersión.

Nota: No existe una única
distribución normal, sino una familia de distribuciones
con una forma común, diferenciadas por los valores de su
media y su varianza. De entre todas ellas, la más
utilizada es la distribución normal
estándar, que corresponde a una distribución
con una media aritmética de 0 y una desviación
típica de 1.
Área bajo
la curva
El área total limitada por la curva y el eje "X"
es 1, por lo tanto, el área bajo la curva entre X = a y X
= b, con a < b, representa la probabilidad de que X
esté entre a y b. Esta probabilidad se denota
por:

Esta probabilidad se ilustra en el siguiente
gráfico elaborado con el programa Winstats.

Ejemplos
ilustrativos
1) Averigüe el área bajo la curva de
distribución normal entre Z = 0,8 y Z = 2,12
Solución:
Realizando el gráfico en Winstats y Paint se
obtiene:
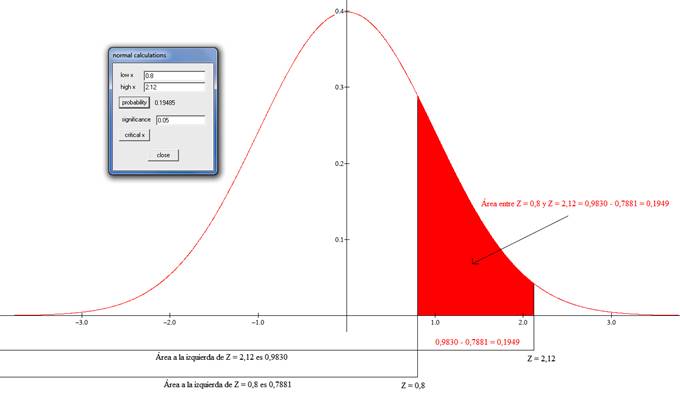
El área a la izquierda de Z = 0,8 con lectura en
la tabla de la distribución normal es 0,7881
El área a la izquierda de Z = 2,12 con lectura en
la tabla de la distribución normal es 0,9830

El área Z = 0,8 y Z = 2,12 es 0,9830 –
0,7881 = 0,1949
Los cálculos en Excel se muestran en la siguiente
figura:

2) Halle Z si el área entre -1,5 y Z es
0,0217
Solución:
Realizando un gráfico ilustrativo en Winstats y
Paint se obtiene:

Los cálculos en Excel se muestran en la siguiente
figura:

3) El peso de 200 estudiantes varones de cierta
universidad es 151 libras, y la desviación típica
es 15 libras. Si los pesos están distribuidos normalmente,
calcular la probabilidad y el número de estudiantes que
pesan Entre 120 y 155 libras
Solución: La curva normal corresponde a
una función continua (valor decimal). Para resolver estos
problemas se emplea los límites inferior y superior
según sea el caso, es decir, para este problema es entre
119,5 y 155,5 libras
Normalizando los datos se tiene:

Graficando se obtiene:

El área a la izquierda de Z = 0,3 con lectura en
la tabla de la distribución normal es 0,6179
El área a la izquierda de Z = -2,1 con lectura en
la tabla de la distribución normal es 0,0179
El área entre -2,1 y 0,3 es 0,6179 – 0,0179
= 0,6 = 60%
El número de estudiantes es 0,6 x 200 =
120
Los cálculos en Excel se muestran en la siguiente
figura:

Autor:
Mario Orlando Suárez
Ibujes