Introducción
Las medidas de dispersión (desviación
media, varianza, desviación estándar, rango,
amplitud intercuartílica, desviación
cuartílica y la amplitud cuartílica) son todas
medidas de variación absolutas. Una medida de
dispersión relativa de los datos, que toma en cuenta su
magnitud, está dada por el coeficiente de
variación.
El Coeficiente de variación (CV) es una
medida de la dispersión relativa de un conjunto de datos,
que se obtiene dividiendo la desviación estándar
del conjunto entre su media aritmética y se expresa
generalmente en términos porcentuales.
Propiedades
– Puesto que tanto la desviación
estándar como la media se miden en las unidades
originales, el CV es una medida independiente de las
unidades de medición.
– Debido a la propiedad anterior el CV es la
cantidad más adecuada para comparar la variabilidad de dos
conjuntos de datos.
Métodos de
cálculo
3.1) Para una población se emplea
la siguiente fórmula:

3.2) Para una muestra se emplea la
siguiente fórmula:

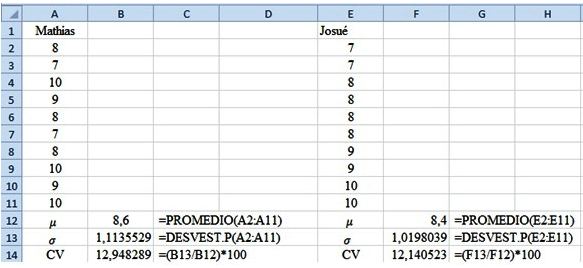
Ejemplo ilustrativo N° 1: Mathías, un
estudiante universitario, tiene las siguientes calificaciones en
las 10 asignaturas que recibe en su carrera: 8, 7, 10, 9, 8, 7,
8, 10, 9 y 10. Josué, un compañero de
Mathías, tiene las siguientes calificaciones: 8, 9, 8, 7,
8, 9, 10, 7, 8 y 10. ¿Cuál estudiante tiene menor
variabilidad en sus calificaciones?
Solución: Como se está tomando en
cuenta todas las asignaturas, se debe calcular el coeficiente de
variación poblacional.
Sin agrupar los datos empleando Excel se calcula el
coeficiente de variación tal como se muestra en la
siguiente figura:
Agrupando los datos en tablas de
frecuencias se calcula así:
a) Se agrupa las calificaciones y se
realiza el cálculo la media aritmética

b) Se calcula la desviación
estándar

c) Se calcula el coeficiente de
variación
Para Mathías se obtiene:

Empleando Excel es como muestra la siguiente
figura:

Para Josué se obtiene:

Empleando Excel es como muestra la siguiente
figura:

Interpretación: Por lo tanto el
estudiante que tiene menor variabilidad en sus calificaciones es
Josué
Ejemplo ilustrativo N° 2: Se saca una muestra
de un curso de la Universidad UTN sobre las calificaciones en las
asignaturas de Matemática y Estadística, resultados
que se presentan en las siguientes tablas. ¿En qué
asignatura existe mayor variabilidad?. Realice los
cálculos empleando Excel

Solución:
Los cálculos para la asignatura de
Matemática empleando Excel se muestran en la siguiente
figura:

Los cálculos para la asignatura de
Estadística empleando Excel se muestran en la siguiente
figura:

Interpretación: Por lo tanto el curso
presenta mayor variabilidad en la asignatura de
Matemática.
Referencias
bibliográficas
SUÁREZ, Mario, (2011), Interaprendizaje de
Estadística Básica,
TAPIA , Fausto Ibarra, Ecuador.
Autor:
Mario Orlando Suárez Ibujes