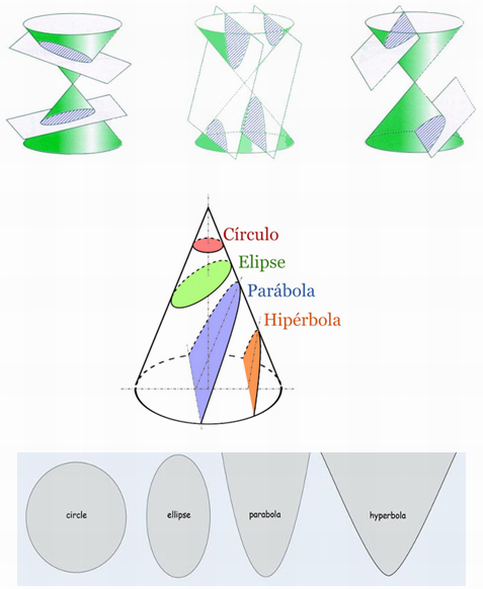
Definición
Las cónicas son curvas planas
obtenidas mediante la intersección de un cono con un
plano. El ángulo que forman el plano y el eje del cono,
comparado con el ángulo que forman el eje y la generatriz
del cono determina las distintas clases de cónicas. Se
clasifican en tres tipos: elipses, parábolas e
hipérbolas.
Hay varias formas de estudiar las
cónicas:
a) Se pueden estudiar como hicieron los
griegos, como has visto en las figuras
anteriores, en términos de
intersecciones del cono con planos.
b) Se pueden estudiar como casos
particulares de ecuaciones de segundo grado con dos variables x e
y
Ax2 +B x y +C y2 +Dx+E y +F = 0
c) Sin embargo , es más adecuado
estudiarlas como lugares geométricos de puntos que cumplen
cierta propiedad geométrica
La
circunferencia
Definición
Una circunferencia es el lugar
geométrico de los P(x, y) que equidistan de un punto fijo
C llamado (centro)
d(P,C) = cte = radio
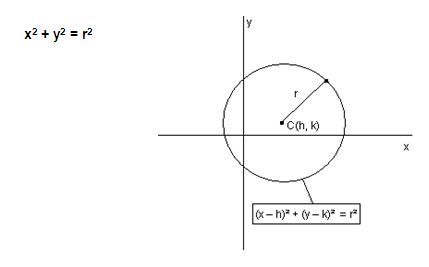
Sea P(x, y) un punto cualquiera verificando
d(P,C) = r, siendo r el radio y C(x0, y0) el centro. De la
formula de la distancia de dos puntos se tiene

Cuando la circunferencia tiene el centro en
el origen se tiene la ecuación reducida
Ecuación vectorial de la
circunferencia
La circunferencia con centro en el origen y
radio R, tiene por ecuación vectorial:

Se puede deducir fácilmente desde la
ecuación cartesiana, ya que el componente X y el
componente Y, al cuadrado y sumados deben dar por resultado el
radio de la circunferencia al cuadrado. En el espacio esta misma
ecuación da como resultado un cilindro, dejando el
parámetro Z libre.
Ecuación en coordenadas polares

Ecuación en coordenadas
paramétricas
La circunferencia con centro en
(a, b) y radio c se parametriza con
funciones trigonométricas como:

Elipse
Una elipse es el lugar geométrico de
los P(x, y) cuya suma de distancias a dos puntos fijos (focos) es
constante
Definiciones:

Observaciones:
i. De hecho, cualquier par de puntos
del plano pueden servir como focos de una elipse. Por
simplicidad, solo se considerarán inicialmente aquellos
casos en los cuales los focos están en el mismo eje (eje
x, eje y) y son simétricos uno del otro con respecto al
origen (fig.

Construcción
de la Elipse
Existen muchas construcciones
geométricas de la elipse, pero en la mayoría de
ellas se requiere conocer algunos elementos adicionales (la
directriz, la excentricidad, …etc.) de la elipse que no han
sido mencionados hasta ahora. Por esta razón, solo se
presentan dos métodos geométricos sencillos para
construir la elipse. Construcción 1
Supóngase que en el plano se tienen
dos puntos fijos F y F". Se toma una cuerda de longitud 2a (mayor
que la distancia entre los focos). Con la punta P de un
lápiz se tensiona la cuerda. Al mover el lápiz
manteniendo en todo momento tensionada la cuerda, el punto P
describe la elipse pedida.

Construcción 2
Supóngase que nos plantean el
problema de construir la elipse de ecuación dada
por

Se procede entonces como sigue:

Se traza luego un rayo cualquiera con
origen en 0, el cual intercepta a los círculos en los
puntos S y N. Por estos puntos, se trazan paralelas a los ejes x
e y respectivamente, las cuales se cortan en el punto M(xm,
ym).

Las leyes de
Kepler
En 1609 Johannes Kepler (1571-1620)
publica, utilizando las observaciones
de su maestro Tycho Brahe, su obra
"Astronomía Nova" en donde enuncia las dos primeras leyes
referente a las ´orbitas de los planetas.
Posteriormente,
en 1619, Kepler publicaria la
tercera.
Primera Ley: Los planetas describen
orbitas elípticas en uno de cuyos focos
está el Sol.
Segunda Ley: Las áreas
barridas por la recta que une el sol con el planeta
son directamente proporcionales a los
tiempos empleados en barrerlas.
Tercera Ley : Los cuadrados de los
periodos de revolucion son proporcionales a los cubos de los
semiejes mayores de las ´orbitas.

Parábola
En matemática, la parábola (del
griego pa?aß???) es la sección cónica
resultante de cortar un cono recto con un plano paralelo a su
generatriz.1
Se define también como el lugar geométrico de
los puntos que equidistan de una recta (eje o directriz) y un
punto fijo llamado foco.
En geometría proyectiva, la parábola se define
como la curva envolvente de las rectas que unen pares de puntos
homólogos en una proyectividad semejante o semejanza.
La parábola aparece en muchas ramas de las ciencias
aplicadas, debido a que las gráficas de ecuaciones
cuadráticas son parábolas. Por ejemplo, la
trayectoria ideal del movimiento de los cuerpos bajo la
influencia de la gravedad.
Definiciones
i. Sea DD una
recta dada del plano y F un punto del plano que no está en
la recta dada. Se define la parábola como el lugar
geométrico de los puntos P del plano cuya distancia al
punto F es igual a la distancia a larecta
DD.
ii. La recta dada DD se llama
DIRECTRIZ y el punto F se llama FOCO (fig. 6.1.1.) Frecuentemente
se hace referencia a la parábola de directriz DD y de foco
F y se denota por PDD-F. Esto
es:

Hipérbola
Una hipérbola es una
sección cónica, una curva abierta de dos ramas
obtenida al cortar un cono recto por un plano oblicuo al eje de
simetría con ángulo menor que el de la generatriz
respecto del eje de revolución.

Ecuaciones de
cónicas
Ecuación de la circunferencia

Ecuación reducida

Ecuación de la elipse


Elipse de eje vertical y centro distinto al origen

Ecuación de la hipérbola

Ecuación reducida

Hipérbola de eje vertical

Hipérbola de eje horizontal y centro distinto al
origen

Donde A y B tienen signos
opuestos.

Ecuación de la parábola

Ecuación reducida de la
parábola

De ejes el de abscisas y de vértice el origen de
coordenadas

De ejes el de ordenadas y de vértice el origen de
coordenadas

Parábola con eje paralelo a OX y vértice
distinto al origen

Parábola con eje paralelo a OY, y vértice
distinto al origen

Aplicaciones
Las curvas cónicas son importantes
en astronomía: dos cuerpos masivos que interactúan
según la ley de gravitación universal, sus
trayectorias describen secciones cónicas si su centro de
masa se considera en reposo. Si están relativamente
próximas describirán elipses, si se alejan
demasiado describirán hipérbolas o
parábolas. También son importantes en
aerodinámica y en su aplicación industrial, ya que
permiten ser repetidas por medios mecánicos con gran
exactitud, logrando superficies, formas y curvas
perfectas
Otra aplicación de las
cónicas es al estudio de los movimientos de los
proyectiles, tiro horizontal y parabólico
Asimismo se utilizan las propiedades de las
cónicas para la construcción de antenas y radares,
sabiendo que cualquier onda que incide sobre una superficie
parabólica, se refleja pasando por el foco.
Conclusiones
En este trabajo hemos podido ampliar
nuestros conocimientos acerca de las cónicas, conocer
mejor las cónicas, como por ejemplo Elipse (Son figuras
geométricas cerradas, formadas por segmentos de recta);
Hipérbola, Lugar geométrico de todos los puntos
para las cuales la diferencia de las distancias a dos puntos
fijos, llamados focos es constante. Una parábola es una
línea que se puede ajustar, en un espacio bidimensional y
en relación a sistema de coordenadas ortonormales, con la
relación y=a.x²+b, o la aplicación de una
transformación que represente un giro, a dicha
relación.
Bibliografía
Leithold, Louis. Matemáticas
previas al cálculo 3ra.
Edición Grupo Mexicano Mepesa 1998
http://conicas.solomatematicas.com/
http://descartes.cnice.mec.es/materiales_didacticos/Conicas_dandelin_d3/conicas.html
http://www.elko.k12.nv.us/webapps/vmd/mathdictionary/htmldict/spanish/vmd/full/c/conicsections.htm
http://math2.org/math/algebra/es-conics.htm
http://personales.unican.es/gonzaleof/Ciencias_1/conicas.pdf
http://www.scribd.com/doc/22029929/Conica
Autor:
Grupo de Radiología 2010
UNMSM
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |