Vibraciones Mecánicas (página 2)

Vibración mecánica: es el movimiento de
vaivén de las moléculas de su cuerpo o sistema
debido a que posee características energéticas
cinéticas y potenciales.

En cualquiera que sea el caso, la excitación es
el suministro de energía. Como ejemplos de
excitación instantánea tenemos el golpeteo de una
placa, el rasgueó de las cuerdas de una guitarra el
impulso y deformación inicial de un sistema masa resorte,
etc.

Como ejemplo de una excitación constante tenemos
el intenso caminar de una persona sobre un puente peatonal, un
rotor desbalanceado cuyo efecto es vibración por
desbalance, el motor de un automóvil, un tramo de
retenedores es una excitación constante para el sistema
vibratorio de un automóvil, etc.

Los grados de libertad: son el número
mínimo de velocidades generalizadas independientes
necesarias para definir el estado cinemático de un
mecanismo o sistema mecánico. El número de grados
de libertad coincide con el número de ecuaciones
necesarias para describir el movimiento. En caso de ser un
sistema holónomo, coinciden los grados de libertad con las
coordenadas independientes.

Grado de libertad.- es el mínimo número de
coordenadas requeridas e independientes para determinar
completamente la posición de todas las partes de un
sistema en un instante.

En mecánica clásica y lagrangiana, la
dimensión d del espacio de configuración
es igual a dos veces el número de grados de libertad
GL, d = 2·GL.

El número de grados de libertad: en
ingeniería se refiere al número mínimo de
números reales que necesitamos especificar para determinar
completamente la velocidad de un mecanismo o el
número de reacciones de una estructura.

Frecuencias Naturales de vibraciones: De cualquier
estructura física se puede hacer un modelo en forma de un
número de resortes, masas y amortiguadores. Los
amortiguadores absorben la energía pero los resortes y las
masas no lo hacen. Como lo vimos en la sección anterior,
un resorte y una masa interactúan uno con otro, de manera
que forman un sistema que hace resonancia a su frecuencia natural
característica. Si se le aplica energía a un
sistema resorte-masa, el sistema vibrará a su frecuencia
natural, y el nivel de las vibraciones dependerá de la
fuerza de la fuente de energía y de la absorción
inherente al sistema. . La frecuencia natural de un sistema
resorte-masa no amortiguado se da en la siguiente
ecuación:

Donde Fn = la frecuencia natural

k = la constante del resorte, o rigidez

m = la masa

De eso se puede ver que si la rigidez aumenta, la
frecuencia natural también aumentará, y si la masa
aumenta, la frecuencia natural disminuye. Si el sistema tiene
absorción, lo que tienen todos los sistemas
físicos, su frecuencia natural es un poco más baja
y depende de la cantidad de absorción.

Un gran número de sistemas
resorte-masa-amortiguación que forman un sistema
mecánico se llaman "grados de libertad", y la
energía de vibración que se pone en la
máquina, se distribuirá entre los grados de
libertad en cantidades que dependerán de sus frecuencias
naturales y de la amortiguación, así como de la
frecuencia de la fuente de energía.

Por esta razón, la vibración no se va a
distribuir de manera uniforme en la máquina. Por ejemplo,
en una máquina activada por un motor eléctrico una
fuente mayor de energía de vibración es el
desbalanceo residual del rotor del motor. Esto resultará
en una vibración medible en los rodamientos del motor.
Pero si la máquina tiene un grado de libertad con una
frecuencia natural cerca de las RPM del rotor, su nivel de
vibraciones puede ser muy alto, aunque puede estar ubicado a una
gran distancia del motor. Es importante tener este hecho en
mente, cuando se hace la evaluación de la vibración
de una máquina. –la ubicación del nivel de
vibración máximo no puede estar cerca de la fuente
de energía de vibración. La energía de
vibración frecuentemente se mueve por largas distancias
por tuberías, y puede ser destructiva, cuando encuentra
una estructura remota con una frecuencia natural cerca de la de
su fuente.

1.2.- CLASIFICACIÓN DE LAS VIBRACIONES
MECÁNICAS.

Toda máquina en funcionamiento, aunque este muy
bien diseñada, ajustada y equilibrada, se ve sometida a
vibraciones en todos sus elementos.

El fenómeno de vibración no es posible
eliminarlo nunca y así lo demuestra la experiencia. Las
razones son varias, fundamentalmente podemos decir que hay
solicitaciones tanto externas como internas a la máquina,
que hacen vibrar a todos sus componentes.

El viento es en el aeromotor el agente externo excitador
fundamental. Internamente, el alternador (campos
magnéticos variables) y todas las
pequeñísimas desalineaciones, holguras,
excentricidades, etc que tienen todos los componentes
mecánicos, son fuentes internas de excitación para
la máquina en conjunto.se produce vibración cuando
a un sistema mecánico se le desplaza de su posición
de equilibrio y se le deja libre, o bien se le somete a una
percusión, o bien se le aplica una fuerza variable con el
tiempo.

En general, podemos definir la vibracion como: todo
desplazamiento oscilante con el tiempo de un elemento o sistema,
alrededor de su posición de equilibrio
estático.

En el problema de vibraciones intervienen las fuerzas
elásticas y las de inercia. El estudio de vibraciones en
un aeromotor se hace necesario porque un nivel excesivo o
anómalo en las mismas puede conducir a:

– alterar las condiciones normales de operación
de la máquina con el perjuicio que ello lleva, de
desajustes y holguras entre elementos con pérdida de
rendimiento y aumento de ruido sonoro. – si la vibración
es muy intensa, pueden producir aflojes de uniones y el fallo
estructural o colapso de la máquina.

– con vibraciones no muy intensas, puede producirse el
fallo con el tiempo de funcionamiento de la máquina, por
fatiga de algunos de sus elementos. Las vibraciones se pueden
clasificar de varias maneras, según el concepto a
estudiar. Una primera clasificación puede ser
en:

Para un sistema vibrando linealmente rige el principio
de superposición y las técnicas matemáticas
son relativamente sencillas y están bien desarrolladas.
Por el contrario las técnicas para sistemas no lineales
son más complicadas y difíciles de aplicar. Los
sistemas tienden a volverse no lineales cuando crece la amplitud
de su oscilación.

También se puede establecer una segunda
clasificación de la siguiente manera:

La vibración puede ser periodica o aleatoria. La
vibración periódica está caracterizada por
su período de tiempo muy bien definido, (su inversa es la
frecuencia), figura 10. En cambio hay vibraciones que no tienen
una forma de onda o período repetible
característico definido. Estas son las llamadas
vibraciones aleatorias o random. Ver figura 1.

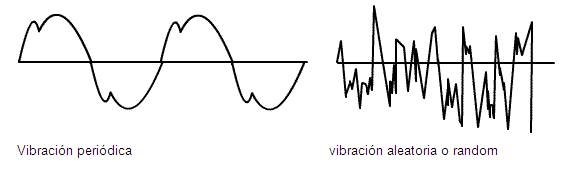
Figura 1

A su vez, la vibración periódica puede
ser: simple y compuesta. Denominamos vibración simple
cuando en el espectro de la misma en frecuencia aparece
únicamente una sola frecuencia. Podemos decir de forma
más coloquial que la vibración simple, sólo
esta compuesta por una onda. Ver figura 2. Si aparecen dos o
más frecuencias en el espectro la vibración es
compuesta.

Figura 2

Toda vibración periódica puede ser
descompuesta en términos de vibraciones simples.
Así pues una vibración compuesta en general, se
puede establecer matemáticamente como la suma de finitos o
infinitos modos propios, según la expresión general
siguiente (6):

6)

Donde n puede ser finito o infinito, según el
tipo de onda. Cada sumando ?n(x) tn(t) constituye el modo propio
i, el cual a su vez consta de la llamada forma propia ?n (x) y la
pulsación propia tn(t). Como ejemplo en la figura 12 se ve
una viga de distribución uniforme, empotrada en un extremo
y libre en el otro, la cual vibra en general con infinitas
formas

Finalmente las vibraciones pueden ser amortiguadas o no
amortiguadas. Como en la realidad todo sistema oscilatorio real
está sometido a cierto grado de amortiguamiento debido a
la fricción y otros tipos de resistencias internas del
propio material, toda vibración "libre" acabará
siendo amortiguada y en el caso de que no fuera amortiguada
sería debido a un aporte externo de energía
(vibración "forzada").

Un caso muy importante en todo sistema vibratorio es
cuando la excitación exterior fuerza al sistema con una
frecuencia exactamente igual a una propia del mismo. Esto se
llama resonancia. En este caso el valor del amortiguamiento y de
la fuerza excitadora es fundamental en el desarrollo de la
vibración, pudiendo darse el caso de rotura de la
estructura del sistema oscilante si el valor relativo del
amortiguamiento es muy bajo.

En el diseño de una máquina debe tenerse
muy en cuenta las posibles resonancias entre los diversos
elementos que la componen, para evitar que en el funcionamiento
de aquella se presenten acoplamientos destructivos entre sus
sistemas oscilantes.

¿Que es vibración?

En su forma más sencilla, una vibración se
puede considerar como la oscilación o el movimiento
repetitivo de un objeto alrededor de una posición de
equilibrio. La posición de equilibrio es la a la que
llegará cuando la fuerza que actua sobre él sea
cero. Este tipo de vibración se llama vibración de
cuerpo entero, lo que quiere decir que todas las partes del
cuerpo se mueven juntas en la misma dirección en cualquier
momento.

El movimiento vibratorio de un cuerpo entero se puede
describir completamente como una combinación de
movimientos individuales de 6 tipos diferentes. Esos son
traslaciones en las tres direcciones ortogonales x, y, y z, y
rotaciones alrededor de los ejes x, y, y z. Cualquier movimiento
complejo que el cuerpo pueda presentar se puede descomponer en
una combinación de esos seis movimientos. De un tal cuerpo
se dice que posee seis grados de libertad. Por ejemplo un barco
se puede mover desde adelante hacia atras ( ondular )desde abajo
hacia arriba ( ) y de babord hacia tribord ( ). También
puede rodar en el sentido de la longitud (rodar), girar alrededor
del eje vertical, (colear) y girar alrededor del eje babor-tribor
(arfar)

Supongamos que a un objeto se le impide el movimiento en
cualquiera dirección excepto una. Por ejemplo un
péndulo de un reloj solamente se puede mover en un plano.
Por eso, se le dice que es un sistema con un grado único
de libertad. Otro ejemplo de un sistema con un grado único
de libertad es un elevador que se mueve hacia arriba y hacia
abajo en el cubo del elevador.

La vibración de un objeto es causada por una
fuerza de excitación. Esta fuerza se puede aplicar
externamente al objeto o puede tener su origen a dentro del
objeto. Mas adelante veremos que la proporción
(frecuencia) y la magnitud de la vibración de un objeto
dado, están completamente determinados por la fuerza de
excitación, su dirección y frecuencia. Esa es la
razón porque un análisis de vibración puede
determinar las fuerzas de excitación actuando en una
máquina. Esas fuerzas dependen del estado de la
máquina, y el conocimiento de sus caracteristicas e
interacciones permite de diagnosticar un problema de la
máquina.

Vibración libre no amortiguada.

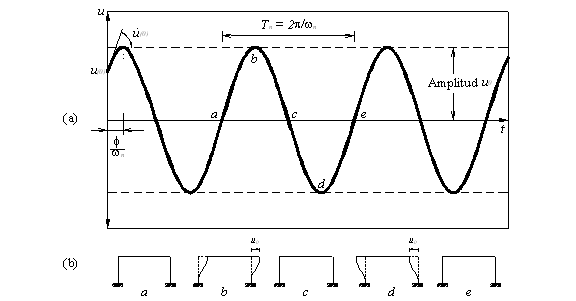
Figura 4.1 sistema sdf: vibración
libre sin amortiguamiento [ref. 12]

 El movimiento representado por la
ecuación 4.5 puede también ser expresado en la
forma: 

Figura 4.2 vibración libre,
representación vectorial [ref. 13]

 Donde u0 es la magnitud del
desplazamiento máximo y es llamada amplitud de movimiento,
la cual esta dada por:

En la figura 4.2 esta representada vectorialmente la
ecuación de movimiento, donde la respuesta esta dada por
la parte real o proyección horizontal de los dos vectores
de rotación; y el ángulo de fase representa la
distancia angular de retraso en la respuesta del término
del coseno.

 Vibración libre con amortiguamiento
viscoso

 La ecuación de movimiento para un sistema
lineal amortiguado en vibración libre es:

El coeficiente de amortiguamiento crítico,
ccr, y la razón o relación de
amortiguamiento crítico, son parámetros que
determinan el tipo de movimiento del sistema.

Figura 4.3 vibración libre de un
sistema críticamente amortiguado, sobreamortiguado y
subamortiguado [ref. 12] 

Las estructuras civiles (puentes, edificios, embalses,
etc.) Poseen una relación de amortiguamiento la cual las
cataloga como sistemas subamortiguados, es por esta razón
que dichos sistemas se estudian con mayor preferencia.

 Sistema subamortiguado

 Para un sistema subamortiguado (C<1)
el desarrollo de la ecuación 4.12 se encuentra en el
apéndice i, y su solución es:

Figura 4.4 efecto del amortiguamiento en
vibración libre

 Nótese que la ecuación
4.15 aplicada a un sistema no amortiguado (C=0) se
reduce a la ecuación 4.5. La figura 4.4 ilustra una
comparación entre un sistema subamortiguado y uno sin
amortiguamiento; se observa que la amplitud del sistema no
amortiguado es la misma en todos los ciclos de vibración,
en cambio para el sistema amortiguado la amplitud decrece y lo
hace en forma exponencial.

El valor del periodo natural de vibración
amortiguado es: 

(4.17)

 Y está relacionado con el
periodo natural sin amortiguamiento de la siguiente
forma:

(4.18)

 La relación entre dos
desplazamientos pico en un intervalo de tiempo td es
constante, y el decremento logarítmico está
definido como el logaritmo natural de esta cantidad y está
dado por:

 (4.19)

 Y la relación entre dos
desplazamientos cuales quiera es:

  (4.20)

1.3 FUENTES DE VIBRACIÓN

  La razón principal para analizar y
diagnosticar el estado de una maquina es determinar las medidas
necesarias para corregir la condición de vibración
– reducir el nivel de las fuerzas vibratorias no deseadas y no
necesarias. De manera que, al estudiar los datos, el
interés principal deberá ser la
identificación de las amplitudes predominantes de la
vibración, la determinación de las causas, y la
corrección del problema que ellas representan.

El siguiente material muestra los diferentes causas de
vibración y sus consecuencias, lo cual nos ayudara
enormemente para interpretar los datos que podamos obtener ,
determinado así el tipo de vibración que se
presenta y buscar así la debida corrección de las
mismas.

Vibración debida a desbalance

El desbalance de la maquinaria es una de las causas
más comunes de la vibración. En muchos casos, los
datos arrojados por un estado de desbalance indican:

• La frecuencia de vibración se manifiesta a 1x
  las rpm de la pieza desbalanceada.

• La amplitud es proporcional a la cantidad de
  desbalance.

• La amplitud de la vibración es normalmente
  mayor en el sentido de medición radial, horizontal o
  vertical (en las maquinas con ejes horizontales).

• El análisis de fase indica lecturas de fase
  estables.

• La fase se desplazará 90º si se desplaza
  el captador 90º.

Nota: el desbalance de un rotor saliente a menudo tiene
como resultado una gran amplitud de la vibración en
sentido axial, al mismo tiempo que en sentido radial.

Vibración debida a falta de
alineamiento

En la mayoría de los casos los datos derivados de
una condición de falta de alineamiento indican lo
siguiente:

• La frecuencia de vibración es de 1x rpm;
  también 2x y 3x rpm en los casos de una grave falta de
  alineamiento.

• La amplitud de la vibración es proporcional a
  la falta de alineamiento.

• La amplitud de la vibración puede ser alta
  también en sentido axial, además de
  radial.

• El análisis de fase muestra lecturas de fase
  inestables.

• La falta de alineamiento, aun con acoplamientos
  flexibles, produce fuerzas tanto radiales como axiales que, a
  su vez, producen vibraciones radiales y axiales.

Nota: uno de los indicios más importantes de
problemas debidos a falta de alineamiento y a ejes torcidos es la
presencia de una elevada vibración en ambos sentidos,
radial y axial. En general, cada vez que la amplitud de la
vibración axial sea mayor que la mitad de la lectura
radial más alta, hay un buen motivo de sospechar la
existencia de un problema de alineamiento o eje
torcido.

Los tres tipos básicos de falta de alineamiento
en el acoplamiento son: angular, en paralelo y una
combinación de ambos.

Una falta de alineamiento angular sujeta principalmente
los ejes de las maquinas accionadora y accionada a
vibración axial igual a la velocidad de rotación
(rpm) del eje.

La falta de alineamiento en paralelo produce
principalmente vibración radial con una frecuencia igual
al doble de la velocidad de rotación del eje.

Vibración debida a excentricidad

La excentricidad es otra de las causas comunes de
vibración en la maquinaria rotativa. Excentricidad en este
caso no significa "ovalización", sino que la línea
central del eje no es la misma que la línea central del
rotor – el centro de rotación verdadero difiere de la
línea central geométrica.

La excentricidad es en realidad una fuente común
de desbalances, y se debe a un mayor peso de un lado del centro
de rotación que del otro.

Una manera de diferenciar entre desbalance y
excentricidad en este tipo de motor es medir la vibración
con filtro afuera mientras el motor está funcionando bajo
corriente. Luego, se desconecta el motor, observando el cambio de
la amplitud de vibración. Si la amplitud se reduce
gradualmente mientras el motor sigue girando por inercia, es muy
probable que el problema sea debido a desbalance; si, en cambio,
la amplitud de vibración desaparece en el momento mismo en
que el motor es desconectado, el problema es seguramente de
naturaleza eléctrica, y es muy posible que se deba a
excentricidad del inducido.

La excentricidad en rodetes o rotores de ventiladores,
sopladores, bombas y compresores puede también crear
fuerzas vibratorias. En esos casos las fuerzas son el resultado
de fuerzas aerodinámicas e hidráulicas desiguales
que actúan contra el rotor.

De elementos rodantes defectuosos

Defectos en las pistas, en las bolas o en los rodillos
de rodamientos de elementos rodantes ocasionan vibración
de alta frecuencia; y, lo que es mas, la frecuencia no es
necesariamente un múltiplo integral de la velocidad de
rotación del eje. La amplitud de la vibración
dependerá de la gravedad de la falla del
rodamiento.

Nota: la vibración generada por el rodamiento
normalmente no es transmitida a otros puntos de la
máquina. Por lo tanto, el rodamiento defectuoso es
generalmente el que se encuentra más cerca del punto donde
ocurre el mayor nivel de vibración de este
tipo.

 Falla de rodamientos – otras causas

Los rodamientos no fallan prematuramente a menos que
alguna otra fuerza actúe sobre ellos; y tales fuerzas son
generalmente las mismas que ocasionan
vibración.

Causas comunes de fallas en los rodamientos de elementos
rodantes:

• Carga excesiva

• Falta de alineamiento

• Defectos de asientos del eje y/o de las
  perforaciones en el alojamiento

• Montaje defectuoso

• Ajuste incorrecto

• Lubricación inadecuada o
  incorrecta

• Sellado deficiente

• Falsa brinelación (deformación bajo
  carga)

• Corriente eléctrica

Vibración debida a rodamientos de chumacera
defectuosos

Elevados niveles de vibración, ocasionados por
rodamientos de chumacera defectuosos, son generalmente el
resultado de una holgura excesiva (causada por desgaste debido a
una acción de barrido o por erosión
química), aflojamientos mecánicos (metal blanco
suelto en el alojamiento), o problemas de
lubricación.

Holgura excesiva de los rodamientos

Un rodamiento de chumacera con holgura excesiva hace que
un defecto de relativamente menor importancia, tal como un leve
desbalance o una pequeña falta de alineamiento, u otra
fuente de fuerzas vibratorias, se transformen como resultado de
aflojamientos mecánicos o en golpes repetidos
(machacado).

En tales casos el rodamiento en si no es lo que crea la
vibración; pero la amplitud de la misma seria mucho menor
si la holgura de los rodamientos fuera correcta.

A menudo se puede detectar un rodamiento de chumacera
desgastado por "barrido" efectuando una comparación de las
amplitudes de vibración horizontal y vertical. Las
maquinas que están montadas firmemente sobre una
estructura o cimentaciones rígidas revelaran, en
condiciones normales, una amplitud de vibración
ligeramente más alta en sentido horizontal.

Torbellino de aceite

Este tipo de vibración ocurre solamente en
maquinas equipadas con rodamientos de chumacera lubricados a
presión, y que funcionan a velocidades relativamente altas
– normalmente por encima de la segunda velocidad critica del
motor.

La vibración debida a torbellinos de aceite a
menudo es muy pronunciada, pero se reconoce fácilmente por
su frecuencia fuera de lo común. Dicha frecuencia
es apenas menor de la mitad de la velocidad de rotación
(en rpm) del eje – generalmente en el orden del 46 al 48% de las
rpm del eje.

El problema de los torbellinos de aceite normalmente se
atribuye a diseño incorrecto del rodamiento, desgaste
excesivo del rodamiento, un aumento de la presión del
lubricante o un cambio de la viscosidad del aceite.

Se pueden hacer correcciones temporales modificando la
temperatura del aceite (viscosidad), introduciendo un leve
desbalance o una falta de alineamiento de manera de aumentar la
carga sobre el eje, o rascando y/o ranurando los costados del
rodamiento, para desbaratar la "cuña" de lubricante. Desde
luego, una solución más duradera es reemplazar el
rodamiento con uno que haya sido diseñado correctamente de
acuerdo a las condiciones operativas de la maquina, o con uno que
esté diseñado para reducir la posibilidad de
formación de torbellinos de aceite.

Los rodamientos con ranuras axiales usan las
ranuras para aumentar la resistencia a la formación de
torbellinos de aceite en tres puntos espaciados uniformemente.
Este tipo de configuración está limitado a las
aplicaciones más pequeñas, tales como turbinas de
gas livianas y turbocargadores.

Los rodamientos de chumacera de lóbulos
brindan estabilidad contra los torbellinos de aceite al
proporcionar tres puntos ce concentración de la
película de aceite bajo presión, que sirven para
centrar al eje.

Los rodamientos de riñón basculante son
comúnmente utilizados para las maquinas industriales
más grandes, que funcionan a velocidades más
altas.

Hay dos causas comunes de vibración que pueden
inducir un torbellino de aceite en un rodamiento de
chumacera:

– vibración proveniente de maquinaria ubicada en
las cercanías: puede ser transmitida al rodamiento de
chumacera a través de estructuras rígidas, tales
como tuberías y cimentaciones. A este fenómeno se
le conoce como torbellino inducido por el
exterior.

– vibración ocasionada por otros elementos de las
maquina misma: toda vez que se detecta la vibración
característica del torbellino de aceite se deberá
realizar una completa investigación de las vibraciones en
toda la instalación, incluyendo las fuentes de
vibración circunvecina, las estructuras de
cimentación y las tuberías relacionadas. Se
podrá así quizás descubrir una causa externa
de los problemas de torbellino de aceite.

Torbellinos de histéresis

Este tipo de vibración es similar a la
vibración ocasionada por el torbellino de aceite, pero
ocurre a frecuencias diferentes, cuando el rotor gira entre la
primera y la segunda velocidad crítica.

Un rotor que funcione por encima de la velocidad
crítica tiende a flexionarse, o asquearse, en sentido
opuesto del punto pesado de desbalance. La amortiguación
interna debida a histéresis, o sea la amortiguación
de fricción, normalmente limita la deflexión a
niveles aceptables. Sin embargo, cuando acontece un torbellino
por histéresis, las fuerzas amortiguadoras se encuentran
en realidad en fase con la deflexión, y por lo tanto,
acrecentan la deflexión del motor.

Cuando dicho rotor está funcionando por encima de
la primera velocidad critica pero por debajo de la segunda, el
torbellino por histéresis ocurre a una frecuencia
exactamente igual a la primera velocidad crítica del
rotor.

Nota: la frecuencia de formación del torbellino
de aceite es levemente menor de la mitad de la velocidad de
rotación del rotor.

La vibración ocasionada por un torbellino por
histéresis tendrá las mismas características
que las ocasionadas por un torbellino de aceite cuando la maquina
funcione a velocidades superiores a la segunda velocidad
crítica del eje. Es decir, que una severa vibración
se producirá a una frecuencia levemente menor que 0.5x las
rpm del rotor.

El torbellino por histéresis es controlado
normalmente por la acción de amortiguación provista
por los rodamientos de chumacera en si. Sin embargo, cuando la
amortiguación estacionaria es baja en comparación
con la amortiguación interna del rotor, es probable que se
presenten problemas.

La solución usual para este problema es aumentar
la amortiguación estacionaria de los rodamientos y de la
estructura de soporte de los mismos, lo que puede lograrse
instalando un rodamiento de riñón basculante o de
algún rodamiento de diseño especial. En algunos
casos el problema puede ser solucionado reduciendo la
amortiguación dada por el rotor – sencillamente, cambiando
un acoplamiento de engranajes con una versión sin
fricción; por ejemplo, con un acoplamiento de disco
flexible.

Lubricación inadecuada

Una inadecuada lubricación, incluyendo la falta
de lubricación y el uso de lubricantes incorrectos, puede
ocasionar problemas de vibración en un rodamiento de
chumacera. En semejantes casos la lubricación inadecuada
causa excesiva fricción entre el rodamiento estacionario y
el eje rotante, y dicha fricción induce vibración
en el rodamiento y en las demás piezas relacionadas. Este
tipo de vibración se llama "dry whip", o sea látigo
seco, y es muy parecido al pasar de un dedo mojado sobre un
cristal seco.

La frecuencia de la vibración debida al
látigo seco generalmente es muy alta y produce el sonido
chillón característico de los rodamientos que
están funcionando en seco. No es muy probable que dicha
frecuencia sea algún múltiplo integral de las rpm
del eje, de manera que no es de esperarse ningún
patrón significativo bajo la luz estroboscópica. En
este respecto, la vibración ocasionada por el
látigo seco es similar a la vibración creada por un
rodamiento antifricción en mal estado.

Toda vez que se sospeche que un látigo seco sea
la causa de la vibración se deberá inspeccionar el
lubricante, el sistema de lubricación y la holgura del
rodamiento.

 Vibración debida a aflojamiento
mecánico

 El aflojamiento mecánico y la acción
de golpeo (machacado) resultante producen vibración a una
frecuencia que a menudo es 2x, y también múltiplos
más elevados, de las rpm. La vibración puede ser
resultado de pernos de montaje sueltos, de holgura excesiva en
los rodamientos, o de fisuras en la estructura o en el pedestal
de soporte.

La vibración característica de un
aflojamiento mecánico es generada por alguna otra
fuerza de excitación, como un desbalance o una falta
de alineamiento. Sin embargo, el aflojamiento mecánico
empeora la situación, transformando cantidades
relativamente pequeñas de desbalance o falta de
alineamiento en amplitudes de vibración excesivamente
altas. Corresponde por lo tanto decir que el aflojamiento
mecánico permite que se den mayores vibraciones de las que
ocurrirían de por sí, derivadas de otros
problemas.

Nota: un aflojamiento mecánico excesivo es muy
probable que sea la causa primaria de los problemas cuando la
amplitud de la vibración 2x las rpm es más de la
mitad de la amplitud a la velocidad de rotación, 1x las
rpm.

Vibración debida a las bandas de
accionamiento

Las bandas de accionamiento del tipo en "v" gozan de
mucha popularidad para la transmisión del movimiento
puesto que tienen una alta capacidad de absorción de
golpes, choques y vibraciones.

Los problemas de vibración asociados con las
bandas en "v" son clasificados generalmente por:

• Reacción de la banda a otras fuerzas,
  originadas por el equipo presente, que causan
  alteraciones.

• Vibraciones creadas por problemas de la banda en
  sí.

Las bandas en "v" son consideradas a menudo como fuente
de vibración porque es tan fácil ver las bandas que
saltan y se sacuden entre poleas. Por lo general, el reemplazo de
las bandas es a menudo una de las primeras tentativas de
corrección de los problemas de
vibración.

Sin embrago es muy posible que la banda esté
sencillamente reaccionando a otras fuerzas presentes en la
maquina. En tales casos las banda es solamente un indicador
de que hay problemas de vibración y no representan la
causa misma.

La frecuencia de vibración de las bandas es el
factor clave en la determinación de la naturaleza del
problema. Si la banda está sencillamente reaccionando a
otras fuerzas de alteración, tales como desbalance o
excentricidad en las poleas, la frecuencia de vibración de
la banda será muy probablemente igual a la frecuencia
alterante. Esto significa que la pieza de la maquina que
realmente está causando el problema aparecerá
estacionaria bajo la luz estroboscópica del
analizador.

Nota: si es defecto de la banda la frecuencia de
vibración será un múltipla integral -1, 2,3
ó 4 – de las rpm de la banda. El múltiplo
verificado dependerá de la naturaleza del problema y de la
cantidad de poleas, sea de accionamiento como locas, presentes en
el sistema.

Es fácil determinar las rpm de una banda de la
siguiente manera:

Rpm de la banda = (3.14 x diám. De la polea x rpm
de la polea)/ longitud de la banda.

 Vibración debida a problemas de
engranaje

La vibración que resulta de problemas de
engranaje es de fácil identificación porque
normalmente ocurre a una frecuencia igual a la frecuencia de
engrane de los engranajes – es decir, la cantidad de dientes
del engranaje multiplicada por las rpm del engranaje que
falla.

Problemas comunes de los engranajes, que tienen como
resultado vibración a la frecuencia de engrane, comprenden
el desgaste excesivo de los dientes, inexactitud de los dientes,
fallas de lubricación y materias extrañas atrapadas
entre los dientes.

No todos los problemas de engranajes generan frecuencias
de vibración iguales a las frecuencias de engrane. Si
un engranaje tiene un solo diente roto o deformado, por
ejemplo, el resultado puede ser una frecuencia de
vibración de 1x las rpm. Mirando la forma de onda de esa
vibración en un osciloscopio conectado con un analizador,
la presencia de señales de impulso permitirá
distinguir entre este problema y las demás averías
que también generan frecuencias de vibración de 1x
las rpm. Desde luego, si hay más de un diente
deformado, la frecuencia de vibración es multiplicada
por una cantidad correspondiente.

La amplitud y frecuencia de vibración debida a
los engranajes pueden también parecer erráticas a
veces. Dicho tipo de vibración errática ocurre
normalmente cuando un conjunto de engranajes está
funcionando en condiciones de carga muy liviana. En tales
condiciones la carga puede desplazarse repetidamente de un
engranaje a otro de modo irregular.

Nota: los problemas de rodamientos son predominantes en
el punto de falla de los mismos, mientras que los problemas de
engranajes pueden ser detectados en dos o más puntos de la
maquina.

Vibración debida a fallas
eléctricas

Esté tipo de vibración es normalmente el
resultado de fuerzas magnéticas desiguales que
actúan sobre el rotor o sobre el estator. Dichas fuerzas
desiguales pueden ser debidas a:

• Rotor que no es redondo

• Chumaceras del inducido que son
  excéntricas

• Falta de alineamiento entre el rotor y el estator;
  entrehierro no uniforme

• Perforación elíptica del
  estator

• Devanados abiertos o en corto circuito

• Hierro del rotor en corto circuito

U N I D A D 2

En líneas generales, la frecuencia de
vibración resultante de los problemas de índole
eléctrica será 1x las rpm, y por tanto se
parecerá a desbalance. Una manera sencilla de hacer la
prueba para verificar la presencia eventual de vibración
eléctrica es observar el cambio de la amplitud de la
vibración total (filtro fuera) en el instante en el cual
se desconecta la corriente de esa unidad. Si la
vibración desaparece en el mismo instante en que se
desconecta la corriente, el problema con toda posibilidad
será eléctrico. Si solo decrece
gradualmente, el problema será de naturaleza
mecánica.

Las vibraciones ocasionadas por los problemas
eléctricos responden generalmente a la cantidad de carga
colocada en el motor. A medida que se modifica la carga, la
amplitud y/o las lecturas de fase pueden indicar cambios
significativos. Esto explica por qué los motores
eléctricos que han sido probados y balanceados en
condiciones sin carga muestran cambios drásticos de los
niveles de vibración cuando vuelven a ser puestos en
servicio.

Análisis
dinámico del sólido rígido, fuerzas y
aceleración

2.1.- PRINCIPIO DE D'ALEMBERT

El principio de d'Alembert, enunciado por Jean
d'Alembert en su obra maestra Tratado de dinámica
de 1743, establece que la suma de las fuerzas externas que
actúan sobre un cuerpo y las denominadas fuerzas de
inercia forman un sistema de fuerzas en equilibrio. A este
equilibrio se le denomina equilibrio
dinámico.

El principio de d'Alembert establece que para todas las
fuerzas de un sistema:

El principio de d'Alembert es realmente una
generalización de la segunda ley de Newton en una forma
aplicable a sistemas con ligaduras. Por otra parte el principio
equivale a las ecuaciones de Euler-Lagrange. Lagrange usó
este principio bajo el nombre de principio de velocidades
generalizadas, para encontrar sus ecuaciones, en la memoria
sobre las libraciones de la Luna de 1764, abandonando desde
entonces el principio de acción y basando todo su trabajo
en el principio de D'Alembert durante el resto de su vida y de
manera especial en su Mécanique Analytique. Tal
cambio de actitud pudo estar influido por dos razones:1

• En primer lugar, el principio de acción
  estacionaria está ligado a la existencia de una
  función potencial, cuya existencia no requiere en el
  principio de d'Alembert.

• En segundo lugar, el principio de acción se
  presta a interpretaciones filosóficas y
  teleológicas que no le gustaban a Lagrange.

Finalmente debe señalarse que el principio de
d'Alembert es peculiarmente útil en la mecánica de
sólidos donde puede usarse para plantear las ecuaciones de
movimiento y cálculo de reacciones usando un campo de
desplazamientos virtuales que sea diferenciable. En ese caso el
cálculo mediante el principio de D'Alembert, que
también se llama en ese contexto principio de los trabajos
virtuales es ventajoso sobre el enfoque más simple de la
mecánica newtoniana.

Consecuencias

El principio de d'Alembert en el caso de existir
ligaduras no triviales lleva a las ecuaciones de Euler-Lagrange,
si se usa conjunto de coordenadas generalizadas independientes
que implícitamente incorporen dichas ligaduras.
Consideremos un sistema de N partículas en el que
existan m ligaduras:

Por el teorema de la Función Implícita
existirán n = 3N-m coordenadas
generalizadas y N funciones vectoriales tales
que:

Si las fuerzas son además conservativas entonces
podemos existe una función potencial U
(Wj) y podemos definir el lagrangiano L = T
– U, simplificando aún más la expresión
anterior.

2.2.- TRASLACION RECTILINEA

La traslación rectilínea se
conceptualiza (define) como un cambio continúo de
posición y el conjunto de posiciones que va ocupando el
cuerpo, traza una trayectoria recta, las características
cinemáticas son:

• -        
  La velocidad y aceleración de dos puntos
  cualesquiera del cuerpo es idéntica.

Entonces, también la velocidad y la
aceleración es la misma para cualquier punto del plano que
representa al cuerpo rígido, desde el punto de vista
cinemático; esto implica que, el plano en
traslación rectilínea, se puede analizar como si
fuera una partícula utilizando las siguientes
formulas:

2.3.-TRASLACION CURVILINEA

Traslación

Figura 3-19

2.4.- ROTACIÓN CENTROIDAL

Se llama rotación centroidal a la rotación
de un cuerpo alrededor de un eje fijo que pasa por su
centro  de masa y es perpendicular al plano de
movimiento.

Figura 3-20

2.5.- ROTACIÓN NO CENTROIDAL

El sistema equivalente para este caso se representa
en la figura 3-21.

Si se toma momentos con respecto a O se tiene , ya
que el momento de es cero. Pero y como entonces

Donde IO es el momento de inercia del cuerpo con
respecto al eje que pasa por O y es perpendicular al plano de
movimiento. A diferencia de la rotación centroidal, la
fuerza resultante en el caso de rotación no centroidal es
diferente de cero ya que el centro de masa posee
aceleración. El hecho de resaltar en la rotación no
centroidal es que la ecuación [3-13] es de la misma forma
que la ecuación [3-11] lo cual no se cumple para cualquier
otro punto. 

2.6.- MOVIMIENTO DE RODADURA

Si un cuerpo rueda sobre otro, puede ocurrir que en el
punto de contacto no haya movimiento relativo, en cuyo caso se
dice que el movimiento es de rodadura pura, o que haya movimiento
relativo; en este caso se habla de rodadura con
deslizamiento.

Figura 3-24

Figura 3-25

Cuando en una situación determinada no se sabe si
hay o no rodadura pura, se supone inicialmente que no hay
deslizamiento, entonces la fuerza de fricción es
desconocida pero se conoce la relación entre aC
 y a.

2.7.- MOVIMIENTO GENERAL EN EL PLANO

La ecuación [3-13] también se cumple en
movimiento plano general en dos casos:

Si se toman  momentos con respecto a un punto que
no tenga aceleración pero que se puede estar
moviendo.

Cuando se toman momentos con respecto a un punto cuya
aceleración está dirigida hacia el centro de
masa.

Veamos:

Si el punto O no tiene aceleración, [Fig. 3-22],
al tomar momentos con respecto a O se tiene

Figura 3-22

Si el punto O tiene aceleración dirigida
hacia C, [Fig. 3-23], la aceleración de C es

Figura 3-23

Tomando momentos con respecto a O se tiene:

U N I D A D 3

Movimiento plano de
un sólido rígido: impulso y cantidad de
movimiento

En mecanica, se denomina impulso a la magnitud
física, generalmente representada como (I), definida como
la variación en la cantidad de movimiento que experimenta
un objeto en un sistema cerrado. El término difiere de lo
que cotidianamente conocemos como impulso y fue acuñado
por Isaac Newton en su segunda ley, donde la llamó vi
motrici refiriéndose a una especie de fuerza del
movimiento.[1]

Definición

En la mecánica clásica, a partir de la
segunda ley de Newton sobre la fuerza tenemos que

si multiplicamos ambos miembros por

lo que nos dice que la variación de la cantidad
de movimiento es proporcional a una fuerza aplicada sobre la
partícula durante un intervalo de tiempo:

A lo que llamamos impulso es ese valor de la integral de
la fuerza en el tiempo:

Unidades

Un impulso cambia el momento lineal de un objeto, y
tiene las mismas unidades y dimensiones que el momento lineal.
Las unidades del impulso en el Sistema Internacional son kg·m/s.

Para deducir las unidades podemos utilizar la
definición más simple, donde tenemos:

Conservación del momento lineal

Como hemos visto, la variación en la cantidad del
movimiento y el impulso van estrechamente ligados. La
conservación de la cantidad de movimiento lineal es una de
las cantidades físicas que en un sistema cerrado aparecen
inalterables. Así, si sobre un sistema no se ejerce fuerza
neta alguna, el momento lineal total del sistema no puede variar.
Y para nuestro caso: para hacer variar la cantidad de movimiento
de un cuerpo es necesario aplicarle un impulso producto de una
fuerza.[2]

Choques

Los choques son interacciones de dos o más
cuerpos en el que existe contacto entre ellos durante un tiempo
tanto determinado como indeterminado. Existen distinos tipos de
choque, los choques elásticos, inelásticos y
totalmente inelásticos. Todos estos choques tienen la
característica de conservar su momentum o cantidad de
movimiento, pero no así su energía mecánica,
que en la mayoría de los casos solo se considera la
energía cinética. Los choques que son
elásticos mantienen el momentum inicial del sistema igual
al final al igual que la energía cinética total del
sistema. Dentro de este tipo de choque es importante mecionar un
caso importantes que es el choque de dos cuerpos de igual masa y
uno de ellos inicialmente en reposo. En el caso de que ambos
cuerpos tengan la misma masa y uno de ellos se encuentra en
reposo, al impactar se transferirá la energía desde
el cuerpo en movimiento hacia el que no se esta moviendo,
quedando el cuerpo inicialmente en movimiento en reposo, mientras
que el otro seguirá en movimiento, el mismo que
seguía el primer cuerpo, un ejemplo de este es el juego de
pool o billar. Mientras dura el choque cabe señalar que en
el contacto de ambos cuerpos la energía se almacena en una
desformación mínima y no permanente.

Choque elástico

En física, en el caso ideal, una colisión
perfectamente elástica es un choque entre dos o más
cuerpos que no sufren deformaciones permanentes debido al
impacto. En una colisión perfectamente elástica se
conservan tanto el momento lineal como la energía
cinética del sistema.

Claro está que durante una colisión,
aunque sean de dos sólidos, no se puede considerar
perfectamente elástico ya que siempre hay una
deformación.

Las colisiones en las que la energía no se
conserva producen deformaciones permanentes de los cuerpos y se
denominan colisiones inelásticas.

Colisiones elásticas son aquellas en las cuales
no hay intercambio de masa entre los cuerpos que colisionan, sin
embargo, hay conservación neta de energía
cinética.

Choque inelástico

En un choque inelástico los cuerpos presentan
deformaciones luego de su separación; esto es una
consecuencia del trabajo realizado. En el caso ideal de un choque
perfectamente inelástico, los objetos en colisión
permanecen pegados entre sí. El marco de referencia del
centro de masas permite presentar una definición
más precisa. En los choques inelásticos la
energía cinética no se conserva, ya que está
es "usada" para deformar el cuerpo.

La cantidad de movimiento, momento lineal, ímpetu
o moméntum es una magnitud vectorial, unidad SI: (kg m/s)
que, en mecánica clásica, se define como el
producto de la masa del cuerpo y su velocidad en un instante
determinado. En cuanto al nombre Galileo Galilei en su
Discursos sobre dos nuevas ciencias usa el
término italiano impeto, mientras que Isaac
Newton usa en Principia Mathematica el término
latino motus[1]
(movimiento) y vis (fuerza). Moméntum es
una palabra directamente tomada del latín
momentum, derivado del verbo movere
'mover'

En Mecánica Clásica la forma más
usual de introducir la cantidad de movimiento es mediante
definición como el producto de la masa (Kg) de un cuerpo
material por su velocidad (m/s), para luego analizar su
relación con la ley de Newton a través del teorema
del impulso y la variación de la cantidad de movimiento.
No obstante, después del desarrollo de la Física
Moderna, esta manera de hacerlo no resultó la más
conveniente para abordar esta magnitud fundamental.

El defecto principal es que esta forma esconde el
concepto inherente a la magnitud, que resulta ser una propiedad
de cualquier ente físico con o sin masa, necesaria para
describir las interacciones. Los modelos actuales consideran que
no sólo los cuerpos masivos poseen cantidad de movimiento,
también resulta ser un atributo de los campos y los
fotones.

La cantidad de movimiento obedece a una ley de
conservación, lo cual significa que la cantidad de
movimiento total de todo sistema cerrado (o sea uno que no es
afectado por fuerzas exteriores, y cuyas fuerzas internas no son
disipadoras) no puede ser cambiada y permanece constante en el
tiempo.

En el enfoque geométrico de la mecánica
relativista la definición es algo diferente.
Además, el concepto de momento lineal puede definirse para
entidades físicas como los fotones o los campos
electromagnéticos, que carecen de masa en reposo. No se
debe confundir el concepto de momento lineal con otro concepto
básico de la mecánica newtoniana, denominado
momento angular, que es una magnitud diferente.

Finalmente, se define el impulso recibido por una
partícula o un cuerpo como la variación de la
cantidad de movimiento durante un periodo de tiempo
dado:

Siendo pf la cantidad de movimiento al final
del intervalo y p0 al inicio del intervalo.

Cantidad de movimiento en mecánica
clásica

Mecánica newtoniana

Históricamente el concepto de cantidad de
movimiento surgió en el contexto de la mecánica
newtoniana en estrecha relación con el concepto de
velocidad y el de masa. En mecánica newtoniana se define
la cantidad de movimiento lineal como el producto de la masa por
la velocidad:

La idea intuitiva tras esta definición
está en que la "cantidad de movimiento" dependía
tanto de la masa como de la velocidad: si se imagina una mosca y
un camión, ambos moviéndose a 40 km/h, la
experiencia cotidiana dice que la mosca es fácil de
detener con la mano mientras que el camión no, aunque los
dos vayan a la misma velocidad. Esta intuición
llevó a definir una magnitud que fuera proporcional tanto
a la masa del objeto móvil como a su velocidad.

Mecánica lagrangiana y hamiltoniana

En las formulaciones más abstractas de la
mecánica clásica, como la mecánica
lagrangiana y la mecánica hamiltoniana, además del
momento lineal y del momento angular se pueden definir otros
momentos, llamados momentos generalizados o momentos conjugados,
asociados a cualquier tipo de coordenada generalizada. Se
generaliza así la noción de momento.

Si se tiene un sistema mecánico definido por su
lagrangiano L definido en términos de las
coordenadas generalizadas (q1,q2,…,qN) y las
velocidades generalizadas, entonces el momento

conjugado de la coordenada qi viene dado
por:

Cuando la coordenada qi es una de las
coordenadas de un sistema de coordenadas cartesianas, el momento
conjugado coincide con una de las componentes del momento lineal,
y, cuando la coordenada generalizada representa una coordenada
angular o la medida de un ángulo, el momento conjugado
correspondiente resulta ser una de las componentes del momento
angular.

Cantidad de movimiento de un medio continuo

Si estamos interesados en averiguar la cantidad de
movimiento de, por ejemplo, un fluido que se mueve según
un campo de velocidades es necesario sumar la cantidad de
movimiento de cada partícula del fluido, es decir, de cada
diferencial de masa o elemento infinitesimal, es
decir

Cantidad de movimiento en mecánica
relativista

La constancia de la velocidad de la luz en todos los
sistemas inerciales tiene como consecuencia que la fuerza
aplicada y la aceleración adquirida por un cuerpo material
no sean colineales en

general, por lo cual la ley de Newton expresada como
F=ma no es la más adecuada. La ley fundamental de la
mecánica relativista aceptada es F=dp/dt.

El Principio de Relatividad establece que las leyes de
la Física conserven su forma en los sistemas inerciales
(los fenómenos siguen las mismas leyes). Aplicando este
Principio en la ley F=dp/dt se obtiene el concepto de masa
relativista, variable con la velocidad del cuerpo, si se mantiene
la definición clásica (newtoniana) de la cantidad
de movimiento.

En el enfoque geométrico de la mecánica
relativista, puesto que el intervalo de tiempo
efectivo

percibido por una partícula que se mueve con
respecto a un observador difiere del tiempo medido por el
observador. Eso hace que la derivada temporal del momento lineal
respecto a la coordenada temporal del observador inercial y la
fuerza medida por él no coincidan. Para que la fuerza sea
la derivada temporal del momento es necesario emplear la derivada
temporal respecto al tiempo propio de la partícula. Eso
conduce a redefinir la cantidad de movimiento en términos
de la masa y la velocidad medida por el observador con la
corrección asociada a la dilatación de tiempo
experimentada por la partícula. Así, la
expresión relativista de la cantidad de movimiento de una
partícula medida por un observador inercial viene dada
por:

donde v2,c2 son respectivamente el módulo al
cuadrado de la velocidad de la partícula y la velocidad de
la luz al cuadrado y ? es el factor de Lorentz.

Además, en mecánica relativista, cuando se
consideran diferentes observadores en diversos estados de
movimiento surge el problema de relacionar los valores de las
medidas realizadas por ambos. Eso sólo es posible si en
lugar de considerar vectores tridimensionales se consideran
cuadrivectores que incluyan coordenadas espaciales y temporales.
Así, el momento lineal definido anteriormente junto con la
energía constituye el cuadrivector momento-energía
o cuadrimomento P:

Los cuadrimomentos definidos como en la última
expresión medidos por dos observadores inerciales se
relacionarán mediante las ecuaciones suministradas por las
transformaciones de Lorentz.

Cantidad de movimiento en mecánica
cuántica

La mecánica cuántica postula que a cada
magnitud física observable le corresponde un operador lineal
autoadjunto llamado
simplemente "observable", definido sobre un dominio de espacio de
Hilbert abstracto. Este espacio de Hilbert representa cada uno de
los posibles estados físicos que puede presentar un
determinado sistema cuántico.

Conservación

Mecánica newtoniana

En un sistema mecánico de partículas
aislado (cerrado) en el cual las fuerzas externas son cero, el
momento lineal total se conserva si las partículas
materiales ejercen fuerzas paralelas a la recta que las une, ya
que en ese caso dentro de la dinámica newtoniana del
sistema de partículas puede probarse que existe una
integral del movimiento dada por:

Mecánica lagrangiana y hamiltoniana

En mecánica lagrangiana «si el
lagrangiano no depende explícitamente de alguna de las
coordenadas generalizadas entonces existe un momento generalizado
que se mantiene constante a lo largo del tiempo»,
resultando por tanto esa cantidad una integral del movimiento, es
decir, existe una ley de conservación para dicha magnitud.
Pongamos por caso que un sistema mecánico tiene un
lagrangiano tiene n grados de libertad y su lagrangiano
no depende una de ellas, por

ejemplo la primera de ellas, es decir:

En mecánica hamiltoniana existe una forma muy
sencilla de ver determinar si una función que depende de
las coordenadas y momentos generalizados da lugar o no a una ley
de conservación en términos del paréntesis
de Poisson. Para determinar esa expresión calculemos la
derivada a lo largo de la trayectoria de una magnitud:

A partir de esa expresión podemos ver que para
«un momento generalizado se conservará constante
en el tiempo, si y sólo si, el hamiltoniano no depende
explícitamente de la coordenada generalizada
conjugada» como se puede ver:

Mecánica relativista

En teoría de la relatividad la cantidad de
movimiento o cuadrimomento se define como un vector P el
producto de la cuadrivelocidad U por la masa (en reposo)
de una partícula:

En relatividad general esta cantidad se conserva si
sobre ella no actúan fuerzas exteriores. En relatividad
general la situación es algo más compleja y se
puede ver que la cantidad de movimiento se conserva para una
partícula si esta se mueve a lo largo de una línea
geodésica. Para ver esto basta comprobar que la derivada
respecto al tiempo propio se reduce a la ecuación de las
geodésicas, y esta derivada se anula si y sólo si
la partícula se mueve a lo largo de una línea de
universo que sea geodésica:

En general para un cuerpo macroscópico
sólido de cierto tamaño en un campo gravitatorio
que

presenta variaciones importantes de un punto a otro del
cuerpo no es posible que cada una de las partículas siga
una línea geodésica sin que el cuerpo se fragmente
o perdiendo su integridad. Esto sucede por ejemplo en regiones
del espacio-tiempo donde existen fuertes variaciones de
curvatura. Por ejemplo en la caída dentro de un agujero
negro, las fuerzas de marea resultantes de la diferente curvatura
del espacio-tiempo de un punto a otro despedazarían un
cuerpo sólido cayendo dentro de un agujero
negro.

Mecánica cuántica

Como es sabido en mecánica cuántica una
cantidad se conserva si el operador autoadjunto que representa a
dicha magnitud u observable conmuta con el hamiltoniano, de modo
similar a como en mecánica hamiltoniana una magnitud se
conserva si el paréntesis de Poisson con el hamiltoniano
se anula. Tomando como espacio de Hilbert del sistema de una
partícula dentro de un potencial una representación
de tipo

Se tiene que:

Por tanto, si el potencial no depende de las coordenadas
xi, entonces la cantidad de movimiento de la
partícula se conserva. Además, la última
expresión es formalmente equivalente a la del caso
clásico en términos del paréntesis de
Poisson. Teniendo en cuenta claro está, que éste es
el hamiltoniano cuántico, y que las cantidades
físicas, no son las mismas que en la mecánica
clásica, sino operadores que representan las cantidades
clásicas (observables).

3.1.- Principio de Impulso y Cantidad de
Movimiento.

Según el principio de masa, si a ésta se
le aplica una fuerza F adquiere una aceleración
a:

F = m.a

Siendo:

F: fuerza [F] = N (Newton)

a: aceleración [a] = m/s ²

m: masa [m] = kg

Multiplicando ambos miembros por el tiempo t en que se
aplica la fuerza F :

F.t = m.a.t

Como:

a.t = v

siendo:

v: velocidad [v] = m/s

t: tiempo [t] = s

Tenemos:

F.t = m.v

Al término F.t se lo denomina impulso de
la fuerza y al término m.v se lo denomina cantidad de
movimiento, entonces, para el primero:

I = F.t

siendo:

I: impulso [I] = kg.m/s

para el segundo:

p = m.v

siendo:

p: cantidad de movimiento [p] = kg.m/s

Para deducir las unidades, tenemos:

F.t = m.v

N.s = kg.m/s N = kg.m/s ²

kg.m/s ².s = kg.m/s

luego:

[I] = [p] = kg.m/s = N.s

El impulso de la fuerza aplicada es igual a la
cantidad de movimiento que provoca,o dicho de otro modo,
el incremento de la cantidad de movimiento de cualquier
cuerpo es igual al impulso de la fuerza que se ejerce sobre
él.

El impulso y la cantidad de movimiento son magnitudes
vectoriales.

Conservación de la cantidad de
movimiento

Si con un cuerpo de masa m1 y velocidad v1 se aplica una
fuerza a otro cuerpo de masa m2 y velocidad v2, como por ejemplo,
en un saque de tenis, en ese instante es aplicable el principio
de acción y reacción y tenemos que:

es decir la masa de la raqueta por su velocidad, en el
momento del choque, debe ser igual a la masa de la pelota de
tenis por la velocidad que adquiere.

Enunciando la Ley de conservación de la cantidad
de movimiento dice:

En cualquier sistema o grupo de cuerpos que
interactúen, la cantidad de movimiento total, antes de las
acciones, es igual a la cantidad de movimiento total luego de las
acciones.

Choque

Se produce choque entre dos cuerpos cuando uno de ellos
encuentra en su trayectoria a otro y produciéndose
contacto físico.

Al producirse el choque también se producen
deformaciones en ambos cuerpos, éstas pueden desaparecer
de inmediato o perdurar. Si las deformaciones desaparecen
rápidamente significa que se ha producido un choque
elástico, por el contrario, si permanecen se ha producido
un choque inelástico o plástico.

En ambos casos ocurre una variación de la
energía cinética que se transformará en
calor que disiparán los cuerpos.

Choque plástico o inelástico

a) Velocidades de igual dirección y
sentido.

Supongamos un cuerpo 1 de masa m1 y velocidad v1 que se
dirige a hacia el cuerpo 2 de masa m2 y

velocidad v2, siendo ambas velocidades de igual
dirección y sentido. Sobre cada cuerpo actuó en el
momento del choque, el impulso que le provocó el otro
cuerpo, entonces hay dos acciones de igual intensidad y sentido
contrario, en consecuencia ambas cantidades de movimiento
serán iguales y de sentido contrario. Luego del choque
ambos cuerpos continúan juntos con una velocidad final
común a ambos.

La velocidad final será:

b) Velocidades de igual dirección y sentido
contrario.

En este caso los cuerpos poseían velocidades de
igual dirección pero de sentido contrario antes del
choque, como en el caso anterior luego del impacto
continúan juntos, con una velocidad final que
estará dada por la diferencia de las cantidades de
movimiento. La velocidad final será:

La velocidad final mantendrá la misma
dirección pero tendrá el sentido de la velocidad
del cuerpo que antes del choque tenga más cantidad de
movimiento.

2 – Choque elástico

• a) Velocidades de igual
  sentido

Durante el choque cada cuerpo recibe una cantidad de
movimiento que es igual a la velocidad perdida por el otro. Al
recuperar su forma inicial, cada uno pierde o gana
respectivamente, la cantidad de movimiento ganada o perdida en el
momento del choque, la velocidad final de cada uno
será:

• b) Velocidades de distinto
  sentido

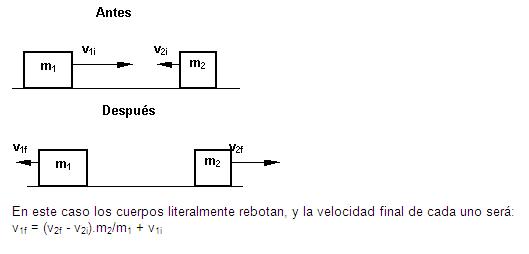
El principio de conservación del impulso es el
mismo que el de conservación de la cantidad de
movimiento.

Cabe aclarar que en la práctica podemos aplicar
el principio de conservación de la cantidad de movimiento
durante los choques, siempre que el tiempo que dura el impacto
sea muy pequeño.

3.2.- Conservación de la cantidad de movimiento
angular.

El momento angular o momento cinético es una
magnitud física importante en todas las teorías
físicas de la mecánica, desde la mecánica
clásica a la mecánica cuántica, pasando por
la mecánica relativista. Su importancia en todas ellas se
debe a que está relacionada con las simetrías
rotacionales de los sistemas físicos. Bajo ciertas
condiciones de simetría rotacional de los sistemas es una
magnitud que se mantiene constante con el tiempo a medida que el
sistema evoluciona, lo cual da lugar a una ley de
conservación conocida como ley de conservación del
momento angular.

Esta magnitud desempeña respecto a las rotaciones
un papel análogo al momento lineal en las traslaciones.
Sin embargo, eso no implica que sea una magnitud exclusiva de las
rotaciones; por ejemplo, el momento cinético de una
partícula que se mueve libremente con velocidad constante
(en módulo y dirección) también se
conserva.

El nombre tradicional en español es momento
cinético,[1]
pero por influencia del inglés angular momentum
hoy son frecuentes momento angular y otras variantes
como cantidad de movimiento angular o ímpetu
angular.

Movimiento angular en mecánica
clásica

En mecánica newtoniana, la cantidad de movimiento
angular de una masa puntual, es igual al producto vectorial del
vector de posición brazo), del objeto en relación a la recta
considerada como eje de rotación, por la cantidad de
movimiento también llamado momento lineal o
momento).
Frecuentemente se lo designa con el símbolo

Matemáticamente, por tanto, es el momento central
de la cantidad de movimiento.

En ausencia de momentos de fuerzas externos, el momento
angular de un conjunto de partículas, de objetos o de
cuerpos rígidos se conserva. Esto es válido tanto
para partículas subatómicas como para
galaxias.

Movimiento angular de una masa puntual

El módulo del momento angular es:

Es decir, el módulo es igual al momento lineal
multiplicado por su brazo ( en el dibujo), el cual es la
distancia entre el eje de rotación y la recta que contiene
la velocidad de la partícula. Por esta razón,
algunos designan el momento angular como el "momento del
momento".

Dependencia temporal

Derivemos el momento angular con respecto al
tiempo:

El primero de los paréntesis es cero ya que la
derivada de con
respecto al tiempo no es otra cosa que la velocidad Y como el vector velocidad
es paralelo al vector cantidad de movimiento el producto vectorial de los
dos es cero.

Nos queda el segundo paréntesis:

donde es
la aceleración. Pero la fuerza aplicada a la masa. Y el producto vectorial
de por la fuerza
es el torque o momento de fuerza aplicado a la masa:

La derivada temporal del momento angular es igual al
torque aplicado a la masa puntual.

La masa gira tenida por un hilo que puede deslizar a
través de un tubito delgado. Tirando del hilo se cambia el
radio de giro sin modificar el momento angular.

En el dibujo de la derecha tenemos una masa que gira,
tenida por un hilo de masa despreciable que pasa por un tubito
fino. Suponemos el conjunto sin rozamientos y no tenemos en
cuenta la gravedad.

La fuerza que el hilo ejerce sobre la masa es radial y
no puede ejercer un torque sobre la masa. Si tiramos del hilo, el
radio de giro disminuirá. Como, en ausencia de torques
externos, el momento angular se conserva, la velocidad de
rotación de la masa debe aumentar.

Vemos como el momento angular se ha conservado: Para
reducir el radio de giro hay que comunicar una velocidad radial,
la cual aumenta la velocidad total de la masa.

También se puede hacer el experimento en el otro
sentido. Si se suelta el hilo, la masa sigue la tangente de la
trayectoria y su momento angular no cambia. A un cierto momento
frenamos el hilo para que el radio sea constante de nuevo. El
hecho de frenar el hilo, comunica una velocidad radial (hacia el
centro) a la masa. Esta vez esta velocidad radial disminuye la
velocidad total y solo queda la componente de la velocidad
tangencial al hilo en la posición en la cual se lo
frenó.

No es necesario de hacer la experiencia dando un
tirón. Se la puede hacer de manera continua, ya que la
fuerza que se hace recobrando y soltando hilo puede descomponerse
en una sucesión de pequeños impulsos.

Conservación del momento angular
cuántico

Es importante notar que si el hamiltoniano no depende de
las variables angulares, como sucede por ejemplo en problemas con
potencial de simetría esférica entonces todas las
componentes del momento angular conmutan con el
hamiltoniano:

y, como consecuencia, el cuadrado del momento angular
también conmuta con el Hamiltoniano:

Y tenemos que el momento angular se conserva, eso
significa que a lo largo de la evolución en el tiempo del
sistema cuántico la distribución de probabilidad de
los valores del momento angular no variará. Nótese
sin embargo que como las componentes del momento angular no
conmutan entre si no se pueden definir simultáneamente.
Sin embargo, si se pueden definir simultáneamente el
cuadrado del momento angular y una de sus componentes
(habitualmente se elije la componente Z). En particular si
tenemos estados cuánticos de momento bien definido estos
seguirán siendo estados cuánticos de momento bien
definido con los mismos valores de los números
cuánticos l y m.

3.3.- Choque excéntrico.

Choque excéntrico. -Si sobre un plano se deja
caer perpendicularmente un cuerpo no elástico, éste
quedará sobre el plano, por aniquilarse la velocidad en el
momento del choque; pero si el plano es de mármol y el
cuerpo de marfil, es decir elásticos, al chocar el cuerpo
contra el plano, la fuerza elástica desarrolla una
acción contraria que destruye la que se pierde por el
choque y como el cuerpo queda con la velocidad de su descenso,
rebota y tiende a elevarse hasta, la misma altura de donde
procedió. Si el cuerpo cae oblicuamente sobre el plano, el
fenómeno en rigor es el mismo, pero se manifiesta de otro
modo. Sea un plano de mármol A B (fig. 53) sobre el cual
cae oblicuamente una esfera de marfil C, al tocar al plano en el
punto n su acción se descompone en dos fuerzas, una
paralela al plano n' y obra perpendicular m' n; esta
última, fuerza se emplea en hacer cambiar de forma al
plano en el primer momento, pero como éste es
elástico, reaccionando sus moléculas, desarrollan
una fuerza igual y contraría a la m n que con la n n', no
destruida, serán fuerzas angulares que tendrán una
resultante n C' en cuya dirección se moverá el
cuerpo hasta llegar a c'. Esta dirección que toma el
cuerpo elástico después del choque se llama
reflexión; el ángulo formado por la
dirección del cuerpo al caer y la normal al plano o sea C
n m, se llama ángulo de incidencia y el formado
por la dirección que toma el cuerpo después del
choque y la misma normal o sea m n C' se llama ángulo
de reflexión. La reflexión de los cuerpos
elásticos se halla sometida a dos leyes:

          1.ª
El ángulo de incidencia es igual al de
reflexión.

          2.ª
Tanto el ángulo de incidencia como el de reflexión
se hallan situados en el mismo plano.

     Varios aparatos se conocen
para demostrar estas leyes: el más sencillo consiste en un
semicírculo dispuesto horizontalmente, (fig. 51) de
madera, cubierta su superficie de bayeta verde y dividido en dos
cuadrantes; en su centro lleva un plano vertical de mármol
negro m. Si se coloca fijo por medio de un tornillo en una de las
divisiones, la 20 por ejemplo, un tubo A provisto de un resorte y
que lleva en su interior una esferita de marfil; lanzada
ésta por la fuerza del resorte contra el plano de
mármol, después del choque irá a parar en B
a la división 20 del otro cuadrante; y lo mismo
sucederá, sea cual fuere la división de donde salga
la esfera que irá a encontrar a la misma división
del lado opuesto. La esfera en sus dos direcciones forma con la
normal al plano de reflexión dos ángulos iguales
como lo demuestran los arcos que abrazan y además se
hallan en el mismo plano como lo manifiesta la disposición
del aparato.

UNIDAD 4

Vibraciones
mecánicas

El aumento permanente de las potencias en
máquinas, junto con una disminución
simultánea de gasto de materiales, y la alta exigencia de
calidad y productividad industrial, hacen que el análisis
dinámico de las vibraciones mecánicas en
máquinas e instalaciones industriales sea cada vez
más exacto.

El Ingeniero debe ser capaz de trabajar sobre
vibraciones, calcularlas, medirlas, analizar el origen de ellas y
aplicar correctivos. Hace más o menos 40 años, la
temática de vibraciones mecánicas se

constituyó en parte integral de la
formación de ingenieros mecánicos en los paises
industrializados.

El fenómeno de las vibraciones mecánicas
debe ser tenido en cuenta para el diseño, la
producción y el empleo de maquinaria y equipos de
automatización. Así lo exige un rápido
desarrollo tecnológico del país.

Aunque este artículo se enfoca hacia las
vibraciones en sistemas mecánicos, el texto y los
métodos analíticos empleados son compatibles con el
estudio de vibraciones en sistemas no
mecánicos.

DEFINICION DE VIBRACIÓN.

No existe una definición bien exacta de
VIBRACION; más sin embargo, se pueden considerar como
vibraciones, las variaciones periódicas temporales de
diferentes magnitudes.

Específicamente, una vibración
mecánica es el movimiento de una película o de un
cuerpo que oscila alrededor de una posición de
equilibrio.

Al intervalo de tiempo necesario para que el sistema
efectúe un ciclo completo de movimiento se le llama
PERIODO de la vibración. El número de ciclos por
unidad de tiempo define la FRECUENCIA del movimiento y el
desplazamiento máximo del sistema desde su posición
de equilibrio se llama AMPLITUD de la
vibración.

3. CAUSAS DE LAS VIBRACIONES MECANICAS.

Son muchas, pero básicamente las vibraciones se
encuentran estrechamente relacionadas con tolerancias de
mecanización, desajustes, movimientos relativos entre
superficies en contacto, desbalances de piezas en rotación
u oscilación, etc.; es decir, todo el campo de la
técnica.

Los fenómenos anteriormente mencionados producen
casi siempre un desplazamiento del sistema desde su
posición de equilibrio estable originando una
vibración mecánica.

CONSECUENCIAS DE LAS VIBRACIONES.

La mayor parte de vibraciones en máquinas y
estructuras son indeseables porque aumentan los esfuerzos y las
tensiones y por las pérdidas de energía que las
acompañan. Además, son fuente de desgaste de
materiales, de daños por fatiga y de movimientos y ruidos
molestos. " Todo sistema mecánico tiene
características elásticas, de amortiguamiento y de
oposición al movimiento; unas de mayor o menor grado a
otras; pero es debido a que los sistemas tienen esas
características lo que hace que el sistema vibre cuando es
sometido a una perturbación ". " Toda perturbación
se puede controlar, siempre y cuando anexemos bloques de control
cuya función de transferencia sea igual o invertida a la
función de transferencia del sistema ". " Si la
perturbación tiene una frecuencia igual a la frecuencia
natural del sistema, la amplitud de la respuesta puede exceder la
capacidad física del mismo, ocasionando su
destrucción

4.1.- Movimiento armónico simple.

El movimiento armónico simple (se abrevia m.a.s.)
es un movimento periódico que queda descrito en
función del tiempo por una función armónica
(seno o coseno). Si la descripción de un movimiento
requiriese más de una función armónica, en
general sería un movimiento armónico, pero no un
m.a.s..

En el caso de que la trayectoria sea rectilínea,
la partícula que realiza un m.a.s. oscila
alejándose y acercándose de un punto, situado en el
centro de su trayectoria, de tal manera que su posición en
función del tiempo con respecto a ese punto es una
sinusoide. En este movimiento, la fuerza que actúa sobre
la partícula es proporcional a su desplazamiento respecto
a dicho punto y dirigida hacia éste.

Elongación

En un movimiento armónico simple la magnitud de
la fuerza ejercida sobre la partícula es directamente
proporcional a su elongación, esto es la distancia
a la que se
encuentra ésta respecto a su posición de
equilibrio.

En un desplazamiento a lo largo del eje Ox, tomando el
origen O en la posición de equilibrio, esta fuerza es tal
que

donde es
una constante positiva y es la elongación.

El signo negativo indica que en todo momento la fuerza
que actúa sobre la partícula está dirigida
hacía la posición de equilibrio; esto es, en
sentido contrario a su elongación (la "atrae" hacia la
posición de equilibrio).

Aplicando la segunda ley de Newton, el
movimiento armónico simple se define entonces en una
dimensión mediante la ecuación
diferencial

(1)

Velocidad