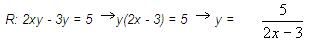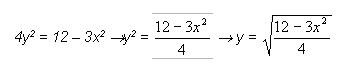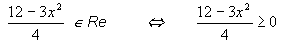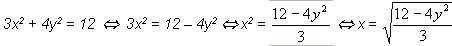Funciones de dos y más variables, dominio y rango, y curva de nivel (página 2)
Ejemplo: Supongamos que tenemos una placa
metálica de grandes dimensiones. La temperatura
(en grados centígrados) de la placa es función de
las coordenadas de cada uno de sus puntos y viene dada
por:
T(x, y) = 500
– 0,6×2 – 1,5y2
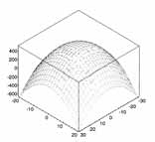
Representación grafica de la
función T(x, y)
Método
para hallar el dominio
Para hallar el dominio
despejamos (y) y analizamos el comportamiento
de (x). Al hacer este despeje podemos considerar tres
casos:
i. La (x) hace parte del denominador de una
fracción. Dé un ejemplo.R: Sea la
relación R = {(x, y) / 2xy - 3y – 5 = 0} definida
en los Reales.ii. Despejar(y)

¿Qué valores
debe tomar (x) (en el denominador) para que sea diferente de
cero?R/:

Cómo se halla el dominio de una
relación, cuando la (x) queda en el denominador al
despejar (y).R: Si al despejar (y) en una
expresión (en una relación), encontramos que la
(x) hace parte del denominador de una fracción,
entonces para determinar el dominio de dicha relación
hay que hacer que el denominador sea diferente de cero y se
despeja la (x).Método
para hallar el RangoComo ya se dijo el rango es el conjunto formado por
aquellos elementos del conjunto de llegada que están
relacionados con algún elemento del conjunto de
partida. Para encontrar el Rango de una relación en
los reales, despejamos (x), analizamos el comportamiento de
(y) y hacemos un análisis similar al que hicimos para
encontrar el dominio.Sea la relación R = {(x, y) / 3×2 + 4y2 =
12}, para ésta hallar el dominio y rango.Con
sólo observar la ecuación diga
¿qué clase de relación real
representa? ¿Por qué?
R: Representa una elipse. Porque los
coeficientes de x2 y de y2 son positivos y
diferentes.Hallar el dominio.

Vemos que la (x) hace parte de un radical
par
Solucionamos una desigualdad
cuadrática
Hallar el rango.R:

La "y" hace parte de un radical par.
Por lo tanto:
Curvas de
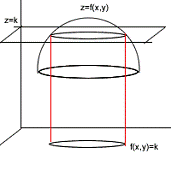
nivelCuando tenemos una función z = f(x, y)
de dos variables
reales y valor
real, la gráfica de dicha función corresponde
al conjunto gr (f):= {(x, y, f(x, y)):
(X, y) ,¬ Dom (f)}. Al ubicar dichos
puntos en el espacio R3, obtenemos una superficie en
dicho espacio.Una forma de estudiar dicha superficie, aunque en
dos dimensiones, es considerar la intersección de
dicha superficie con el plano z = k, donde k
,¬ Recorrido (f). De esta
manera, obtenemos el conjunto {(x, y, k): f(x, y) =
k}, el cual corresponde a la curva de nivel de la
superficie z = f(x, y) con z =
k. Al proyectar dicha intersección en el
planox,y, obtenemos lo que se denomina
curva de nivel.Cuando comparamos una superficie z = f(x,
y) con una montaña, el estudio de las curvas
de nivel corresponde a lo que acontece de manera
análoga cuando dicha montaña es representada en
dos dimensiones por medio de un mapa, donde se dibujan los
contornos de dicha montaña indicando cual es la altura
en las coordenadas (x, y) de dicho
contorno.
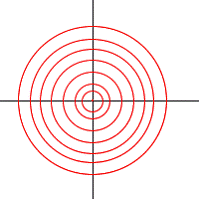
Ejemplo 1. Consideremos la
función z = x2 + y2. Tomando k > 0,
la curva de nivel correspondiente a z = k es la
circunferencia x2 + y2 = k y tomando k
= 0 la curva de nivel corresponde a la descrita por
los puntos (x, y) tales que x2 + y2 =
0 (que corresponde únicamente al punto (0,
0))
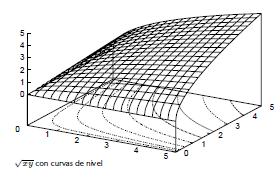
Sea g(x, y) = vxy la media geométrica
de los números x e y.
La curva de nivel 4 está formada por todos los pares
de ordenados (x, y), la media
geométrica de los cuales es 4.Por ejemplo, (4, 4), (2, 8) y
(8, 2) están todos sobre esta curva de nivel.
A continuación mostramos la
gráfica de vxy y sus curvas de nivel
en el plano xy.
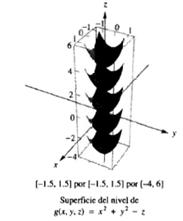
Consideramos ahora la función
f(x, y) = x2 + y2. La curva de nivel 4
está formada portodos los pares (x, y) que
cumplen:f (x, y) = x2 + y2 =
4.Puede que algunos de vosotros hayáis visto
antes que la ecuación describe la circunferencia de
radio 2(2
=v4) centrada en el origen de coordenadas.A continuación mostramos la gráfica de
x2 + y2, así como diferentes curvas de nivel
de la función.
Así pues, podemos resumir:
Dada una función f con
dominio en R2 y un número cualquiera c, la
curva de nivel c de la función
f está formada por el conjunto de
puntos que satisfacen f(x1, x2) =
c.Bibliografía
1. Calculo leithold, Luois leithold, 7
edición, 1998, GRUPO MEXICANO MAPASA
S.A.2. CURVAS DE NIVEL
PEDRO H. ZAMBRANO R, Departamento de
Matemáticas, Universidad Nacional de Colombia,
Bogotá (Colombia) , E-mail address:3. Stewart, James.
Cálculo Multivariable. Cuarta edición.
Thomson Learning.2002.4. FUNCIONES DE VARIAS
VARIABLES (),
20085. CALCULO CON GEOMETRIA
ANALITICA, segunda edición, Earl Swokowski,
Marquette university, Grupo Editorial
Iberoamérica, 1998.6. Calculo de varias
variables, McCullan, Editorial Mc Graw Hill, New
Jersey, 1992.
Autor:
Marlon Fajardo
Molinares2009
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |