Objetivo
El objetivo de
esta experiencia es observar y analizar el comportamiento
de diferentes cuerpos rígidos al rodar, sin deslizar, por
un plano inclinado, y relacionar ese comportamiento a la masa y
al momento de inercia de dichos cuerpos.
Introducción
En este trabajo
observaremos el comportamiento de diferentes cuerpos
rígidos al rodar, sin deslizar, por un plano inclinado y
analizaremos de qué variables
dependen las velocidades con las que llegan a la base del
mismo.
Para ello realizaremos un planteamiento dinámico
y otro energético respecto a un eje instantáneo de
rotación.
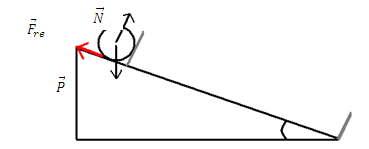
Fig 1. Esquema del dispositivo
utilizado
Analizaremos el movimiento del
cuerpo rígido como un movimiento de roto
traslación. Así, el movimiento de este puede
representarse como una combinación de un movimiento
traslacional del centro de masa y una rotación alrededor
de un eje que pasa por el centro de masa.
Un caso importante de traslación y
rotación combinadas es el de rodar sin deslizar, como por
ejemplo el movimiento de un disco. Si el disco es
simétrico y homogéneo, entonces su centro de masa
coincide con el centro de gravedad en las proximidades de la
superficie terrestre. Observamos que el punto del disco que toca
la superficie en un punto P debe estar instantáneamente en
reposo para que no deslice.
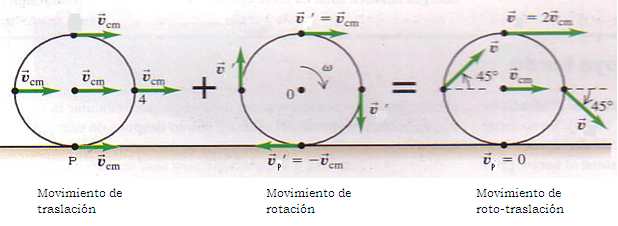
Fig 2. En la figura se muestra la suma
de las velocidades de traslación y de
rotación
de un cuerpo extenso, dando como
resultado la velocidad de
roto traslación.



Como la fuerza de
rozamiento es estática,
el cuerpo está en reposo instantáneo, por lo tanto
la fuerza de rozamiento no realiza trabajo.
Si nuestro sistema de
referencia es:

nos queda:

Este planteamiento lo utilizaremos para calcular la
velocidad final del centro de masa de forma teórica y ver
su dependencia de las masas y los momentos de inercia de cada
cuerpo.
Ahora realizaremos un planteamiento dinámico de
un movimiento traslacional y rotacional combinado de un cuerpo
rígido. Sabemos que para un cuerpo de masa total M, la
aceleración del centro de masa () es igual a la de una
masa puntual M sobre la que actúan todas las fuerzas
externas a las que está sujeto el cuerpo:

El movimiento rotacional alrededor del centro de masa se
describe mediante el análogo rotacional de la segunda
ley de
Newton,
según la ecuación:

donde

Si:

Tenemos:

Podemos observar que la ecuación (27) es igual,
como se esperaba, a la ecuación (10).
Para considerar las distintas variables diseñamos
el siguiente dispositivo experimental.
Materiales:
Plano inclinado de (84,6 ( 0,3) cm de
longitudBalanza con una incerteza de ( 0,0001 kg
Calibre con una incerteza de ( 0,05 mm
Cronómetro con una incerteza de ( 0,01
sDiversos cuerpos rígidos
Cinta métrica
Procedimiento experimental:
Primera parte:
En la primera parte se utilizó un plano
inclinado, por el que se dejaron rodar cuerpos rígidos de
masas similares, pero distintas formas, y por medio de un
cronómetro se midieron los tiempos que tardaron en llegar
a la base del mismo.
Con este tiempo
calculamos cual es la velocidad final del centro de masa del
cuerpo a partir de la ecuación (23).
Segunda parte:
Por el mismo plano inclinado se dejaron rodar diferentes
cuerpos rígidos de masas distintas e igual forma (no
así sus dimensiones), tomando también el tiempo que
tardaron en llegar a la base para poder calcular
mediante la ecuación (23) la velocidad final del centro de
masa.
Tercera parte:
Página siguiente  |