Distribuciones de frecuencia (página 2)

La marca de clase es el
punto medio del intervalo de clase y se obtiene sumando los
límites
inferior y superior de la clase y dividiendo por 2. Así,
la marca de clase del intervalo 60 – 62 es (60 + 62)/2 = 61. La
marca de clase se llama también punto medio de la
clase.

Para análisis matemáticos posteriores, todas las
observaciones pertenecientes a un intervalo de clase dado se
suponen coincidentes con la marca de clase. Así, todas las
alturas en el intervalo de clase 60 – 62 pulgadas se
considerarán como de 61 pulgadas.

Reglas generales
para formar las distribuciones de frecuencia

l. Determinar el mayor y el menor entre los datos registrados
y así encontrar el rango (diferencia entre el mayor y el
menor de los datos).

2. Dividir el rango en un número conveniente de
intervalos de clase del mismo tamaño. Si esto no es
posible, utilizar intervalos de clase de diferente tamaño
o intervalos de clase abiertos. El número de intervalos de
clase se toma generalmente entre 5 y 20 dependiendo de los datos.
Los intervalos de clase se eligen también de forma que las
marcas de
clase o puntos medios
coincidan con datos realmente observados. Esto tiende a aminorar
el llamado error de agrupamiento, en los análisis
matemáticos posteriores. Sin embargo, los límites
reales de clase no coincidirán con los datos
observados.

3. Determinar el número de observaciones que caen
dentro de cada intervalo de clase, es decir, encontrar las
frecuencias de clase. Lo mejor para esto es utilizar una hoja
de conteo.

HISTOGRAMAS Y POLIGONOS DE FRECUENCIA son dos
representaciones gráficas de las distribuciones de
frecuencia.

1. Un histograma o histograma de
frecuencias consiste en una serie de rectángulos que
tienen

(a) Sus bases sobre un eje horizontal (el eje
X) con centros en las marcas de clase y longitud igual
al tamaño de los intervalos de clase.

(b) Superficies proporcionales a las
frecuencias de clase.

Si los intervalos de clase tienen todos igual
tamaño, las alturas de los rectángulos son
proporcionales a las frecuencias de clase y se acostumbra en tal
caso a tomar las alturas numéricamente iguales a las
frecuencias de clase. Si los intervalos de clase no son de igual
tamaño, estas alturas deberán ser
calculadas.

2. Un polígono de frecuencias es un
gráfico de línea trazado sobre las marcas de clase.
Puede obtenerse uniendo los puntos medios de los techos de los
rectángulos en el histograma.

El histograma y el polígono de frecuencias
correspondiente a la distribución de frecuencias de las alturas
de los estudiantes se muestran en el mismo sistema de ejes
en la Fig.1. Se acostumbra a prolongar el polígono con
PQ y RS hasta las marcas de clase inferior y
superior inmediatas, que corresponderían a la clase de
frecuencia cero. En tal caso, la suma de las áreas de los
rectángulos del histograma es igual al e área total
limitada por el polígono de frecuencias y el eje
X.

Distribuciones de
frecuencia relativa

La frecuencia relativa de una clase es la
frecuencia de la clase dividida por el total de frecuencias de
todas las clases y se expresa generalmente como porcentaje. Por
ejemplo, la frecuencia relativa de la clase 66 – 68 de la Tabla 1
es 42/100 = 42 %. La suma de las frecuencias relativas de todas
las clases es evidentemente 1 ó 100 %.

Si las frecuencias en la anterior tabla de frecuencias
se sustituyen por las correspondientes frecuencias relativas, la
tabla resultante se llama distribución de frecuencias
relativas, distribución porcentual o tabla de
frecuencias relativas.

Las representaciones gráficas de distribuciones
de frecuencia relativa pueden obtenerse del histograma o del
polígono de frecuencias, sin más que cambiar la
escala vertical
de frecuencia a frecuencia relativa, conservándose
exactamente el mismo diagrama. Los
gráficos que resultan se llaman
histogramas de frecuencias relativas o histogramas
porcentuales y polígonos de frecuencias
relativas o polígonos porcentuales,
respectivamente.

Distribuciones de
frecuencia acumulada. Ojivas

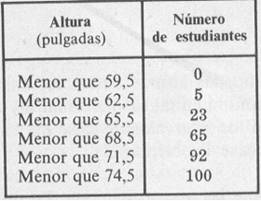
La frecuencia total de todos los valores
menores que el límite real superior de clase de un
intervalo de clase dado se conoce como frecuencia
acumulada hasta ese intervalo de clase inclusive. Por
ejemplo, la frecuencia acumulada hasta el intervalo de clase 66 –
68 inclusive en la Tabla 1, es 5 + 18 + 42 = 65, significando que
65 estudiantes tienen alturas menores que 68,5
pulgadas.

Una tabla que represente las frecuencias acumuladas se
llama distribución de frecuencias acumuladas, tabla de
frecuencias acumuladas o brevemente distribución
acumulada, y se muestra en la
Tabla 2, para la distribución de la altura de los
estudiantes.

Un gráfico que muestre las frecuencias acumuladas
menores que cualquier límite real superior de clase
trazado sobre los límites reales superiores de clase se
llama polígono de frecuencias acumuladas u
ojiva y se muestra en la Fig. 2-2 para la
distribución de la altura de los estudiantes.

En algunos casos es preferible considerar una
distribución de frecuencias acumuladas de todos los
valores
mayores o iguales al límite real inferior de clase de cada
intervalo de clase. En este caso consideramos las alturas de 59,5
pulgadas o más, 62,5 pulgadas o más, etc.,
ésta se llama a veces distribución acumulada
«o más», mientras que la considerada
anteriormente es la distribución acumulada
«menor que». De la una se obtiene
fácilmente la otra. Las correspondientes ojivas se llaman
«o más» y «menor que». Siempre que
nos refiramos a distribuciones acumuladas u ojivas sin
especificar, se entenderá que son del tipo «menor
que».

DISTRIBUCIONES DE FRECUENCIAS RELATIVAS ACUMULADAS.
OJIVAS PORCENTUALES

La frecuencia relativa acumulada o
frecuencia porcentual acumulada es la frecuencia
acumulada dividida por la frecuencia total. Por ejemplo, la
frecuencia relativa acumulada de alturas menores que 68,5
pulgadas es 65/100 = 65 %, queriendo con ello decir que el 65 %
de los estudiantes tienen alturas menores de 68,5
pulgadas.

Si se utilizan en la Tabla 2, y Fig. 2, las frecuencias
relativas acumuladas en lugar de las frecuencias acumuladas, los
resultados se llaman distribuciones de frecuencias relativas
acumuladas o distribuciones porcentuales acumuladas
y polígonos de frecuencias relativas acumuladas u
ojivas porcentuales, respectivamente.

CURVAS DE FRECUENCIAS. OJIVAS
SUAVIZADAS

El conjunto de datos puede considerarse normalmente como
perteneciente a una muestra extraída de una población grande. A causa de las muchas
observaciones que podemos realizar en la población es
posible teóricamente (para datos continuos) elegir los
intervalos de clase muy pequeños y todavía tener un
número adecuado de observaciones dentro de cada clase.
Así se tiene que el polígono de frecuencias o el de
frecuencias relativas para una población grande puede
estar formado por muchos pequeños segmentos rectos que
aproximan el conjunto a una curva, las curvas de este tipo pueden
llamarse curvas de frecuencias o curvas de
frecuencias relativas, respectivamente.

Es razonable esperar que tales curvas teóricas
provengan de la suavización de los polígonos de frecuencias o de los
polígonos de frecuencias relativas de la muestra, la
aproximación es tanto más exacta conforme aumenta
el tamaño de la muestra. Por esta razón una curva
de frecuencias se conoce como un polígono de
frecuencias suavizado.

De una forma análoga las ojivas
suavizadas provienen de la suavización de los
polígonos de frecuencias acumuladas u ojivas. Normalmente
es más sencillo suavizar una ojiva que un polígono
de frecuencias.

Tipos de curvas
de frecuencia

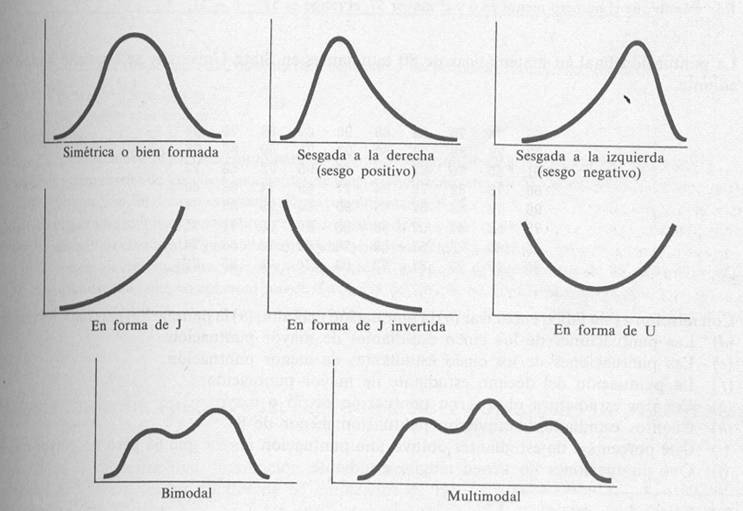
Las curvas de frecuencia presentan determinadas formas
características que les distinguen como se indica en la
Figura 3.

(a) Las curvas de frecuencia
simétricas o bien formadas se
caracterizan por el hecho de que las observaciones que equidistan
del máximo central tienen la misma frecuencia. Un ejemplo
importante es la curva normal.

(b) En las curvas de frecuencia
moderadamente asimétricas o sesgadas la
cola de la curva a un lado del máximo central es mayor que
al otro lado. Si la cola mayor se presenta a la derecha de la
curva se dice que ésta está sesgada a la
derecha o que tiene sesgo positivo, mientras que si
ocurre lo contrario se dice que la curva está sesgada
a la izquierda o que tiene un sesgo
negativo.

(c) En las curvas en forma de J o de
J invertida, el máximo se presenta en un
extremo.

(d) Las curvas de frecuencias en forma de U
tienen el máximo en ambos extremos.

(e) Una curva de frecuencias bimodal
tiene dos máximos.

(f) Una curva de frecuencias multimodal tiene
más de dos máximos.

Bibliografía

Estadística, Teoría
y Problemas
Resueltos.

Murray R. Spiegel.

McGraw-Hill

México, 1983.

Páginas: 27 – 31

Autor:

Martin del Campo Becerra Gustavo
Daniel