Centro de Gravedad (Laboratorio de Física) (página 2)

Por ejemplo para una barra homogénea de longitud
L orientada hacia un planeta lejano, y cuyo centro de gravedad
distan del centro de gravedad del planeta una
distancia

el centro de gravedad de la barra está situado a
una distancia del centro del planeta dada por:

• Ecuaciones
  para líneas, áreas, volúmenes,
  pesos

• ÁREAS:

• VOLÚMENES:

• PESOS:

• Equilibrio: se dice que un cuerpo
  está en equilibrio si este permanece en reposo o en
  movimiento con velocidad constante. Un cuerpo se encuentra en
  equilibrio cuando no sufre cambio ni en su estado de reposo
  ni en su movimiento de traslación ni en el de
  rotación. en consecuencia se dice que un cuerpo
  está en equilibrio:

1.- cuando está en reposo o se mueve con movimiento
uniforme; y

2.- cuando no gira o lo hace con velocidad
constante.

• Equilibrio estable, se da cuando la forma
  cuadrática Q(x1,…, xn ) es definida positiva y, por
  tanto, todos sus autovalores son números positivos. El
  equilibrio es estable si el cuerpo, siendo apartado de su
  posición de equilibrio, vuelve al puesto que antes
  tenía, por efecto de la gravedad. En este caso el
  centro de gravedad está debajo del punto de
  suspensión. Este objeto muestra el concepto de
  equilibrio estable a partir de la visualización de una
  esfera sobre una superficie cóncava. Se evidencia el
  equilibrio estable en el momento en que se aplica la fuerza
  que desplaza la esfera y ésta regresa a su
  posición inicial.

Ejemplo: El péndulo, la plomada, una
campana colgada.

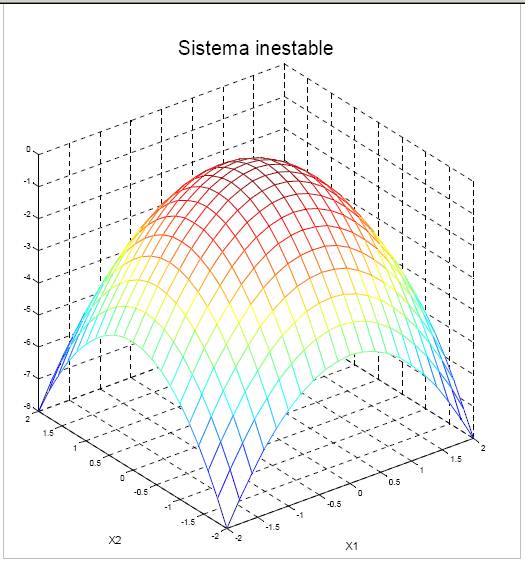
• Equilibrio inestable, se da cuando la forma
  cuadrática Q(x1,…,xn) es definida
  negativa, por tanto, todos sus auto valores son negativos. El
  equilibrio es inestable si el cuerpo, siendo apartado de su
  posición de equilibrio, se aleja por efecto de la
  gravedad. En este caso el centro de gravedad está
  más arriba del punto o eje de
  suspensión.

Ejemplo: Un bastón sobre su
punta.

• Equilibrio indiferente, se da
  cuando la forma cuadrática
  Q(x1,…,xn) es no es definida positiva y
  alguno de sus auto valores es negativo. Esto implica que
  según ciertas direcciones puede haber estabilidad
  unidimensional pero según otras habrá
  inestabilidad unidimensional. El equilibrio es indiferente si
  el cuerpo siendo movido, queda en equilibrio en cualquier
  posición. En este caso el centro de gravedad coincide
  con el punto de suspensión.

• Procedimiento

• Insertar un hilo inextensible por cualquiera de los
  agujeros en las figuras de triplay. Se cuelga el cuerpo
  mediante el hilo y cuando a quedado en reposo se traza le
  vertical que pasa por el punto de suspensión con una
  tiza.

• Se cuelga nuevamente el cuerpo por cualquiera de los
  otros agujeros y se traza la nueva vertical, que en su punto
  de intersección con la anterior vertical determina el
  centro de gravedad del cuerpo. Anote las coordenadas del
  centro de gravedad respecto a un eje horizontal y otro
  vertical. Es preferible tomar estos ejes con tal de que se
  confunda con la figura.

• Tomar las dimensiones de las diferentes partes que
  componen la figura con respecto a los ejes horizontales y
  verticales escogido anteriormente, para hacer este
  último se copia la figura en un papel de tamaño
  adecuado.

–
– – –

FIGURA 1- -FIGURA 2

FIGURA 3

• Datos
  experimentales

• Resultados

Calcular el centro de gravedad de las figuras anteriores
usando las formulas para determinar el centro de gravedad de
áreas.

• PARA LA FIGURA 1:

• PARA LA FIGURA 2:

• PARA LA FIGURA 3:

• Cuestionario

• ¿Explique porque la intersección de
  las líneas horizontales y verticales es el centro de
  gravedad de los cuerpos?

Porque el centro de gravedad debe de coincidir con el
centro de simetría, si un cuerpo tiene un centro de
simetría tal como en las figuras de arriba mencionados el
centro de gravedad coincide con él. Si el cuerpo tiene un
eje de simetría tal como un cono u otra figura, el centro
de gravedad se halla sobre el eje.

OBSERVACIONES :

Con las figuras que hemos trabajado realmente no hay
exactitud en el centro de

Gravedad si existe la diferencia, y siempre varia pero
solamente con la mínima

Diferencia.

• Conclusiones

• Los resultados obtenidos en laboratorio sirve para
  poder comprobar los datos teóricos con los
  prácticos porque a simple vista se observa los errores
  que se cometen al realizar una práctica.

• Se comprobó con las figuras que trabajamos
  existen una mínima diferencia en los resultados del
  centro de gravedad.

• Bibliografía

• Al varenga, Beatriz Física I

• Goldemberg Física fundamental T-I

• Negro Física experimental

• Física – Maiztegui &
  Sabato – Edición 1

• Revista Investigación y Ciencia
  – Jean Michael & É. Kierlik – Julio
  2002

• Física, Curso Elemental:
  Mecánica – Alonso Marcelo

• Física – Wilson
  Jerry

• Cuestiones de Física –
  Aguilar Jsement

• Física Tomo I – Serway
  Raymond

• Dinámica II: Mecánica
  Para Ingeniería y sus Aplicaciones – David J.
  MacGill & Wilton King

• Michel Valero Física Fundamental
  Vol.-1

• Alonso –Finn Física Vol.-1

• Sears –Zemansky –Young Física
  Universitaria

• http://fisica.usach.cl/~lhrodrig/fisica1/estatica.pdf

Autor:

Víctor Acasio Quispe

Profesor:Lic. Bustamante Rodríguez,
Jaime

26 de mayo del 2009

AYACUCHO – PERÚ

Universidad Nacional de San Cristóbal de
Huamanga

Facultad de Ingeniería de Minas, Geología y
Civil

Escuela de Formación Profesional de
Ingenería de Minas