Partes: 1, 2

Estas propiedades pueden ser usadas para extender G(z) desde su definición inicial a todo el plano complejo (exceptuando los puntos en los cuales es singular) por continuación analítica.

Definiciones alternativas

Las siguientes definiciones de la función Gamma mediante productos infinitos, debidas a Euler y Weierstrass respectivamente, son válidas para todo complejo z que no sea un entero negativo:

donde γ es la constante de Euler-Mascheroni.

Es sencillo mostrar que la definición de Euler satisface la ecuación funcional dada arriba como sigue. Dado

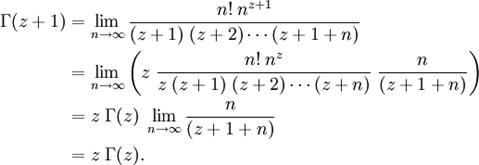
También puede obtenerle la siguiente representación integral:

Obtención de la ecuación funcional usando integración por partes:

Obtener G(1) es sencillo:

Ahora obtendremos una expresión para G(n + 1) como una función de G(n):

Usamos integración por partes para resolver la integral:

En el límite inferior se obtiene directamente:

En el infinito, usando la regla de L'Hôpital:

Por lo que se anula el primer término, lo que nos da el siguiente resultado:

La parte derecha de la ecuación es exactamente nG(n), con lo que hemos obtenido una relación de recurrencia:

G(n + 1) = nG(n).

Apliquemos la fórmula a unos pocos valores:

Propiedades

General

De la representación integral se obtiene:

Otras ecuaciones funcionales importantes de la función Gamma son la fórmula de reflexión de Euler:

y la fórmula de duplicación:

La fórmula de duplicación es un caso especial del teorema de multiplicación:

Una propiedad básica y muy útil de la función Gamma, que puede obtenerse a partir de la definición mediante productos infinitos de Euler es:

Quizá el valor más conocido de la función Gamma con argumento no negativo es

La cual puede obtenerse haciendo z = 1 / 2 en la fórmula de reflexión o en la fórmula de duplicación, usando la relación de la función Gamma con la función beta dada más abajo con x = y = 1 / 2 o haciendo la sustitución en la definición integral de la función Gamma, con lo que se obtiene una integral Gaussiana. En general, para valores impares de n se tiene:

(n: impar)

donde n!! denota al doble factorial.

Las derivadas de la función Gamma vienen dadas por la función poligamma. Por ejemplo:

A partir de la representación integral de la función Gamma, se obtiene que su derivada n-ésima es:

La función Gamma tiene un polo; polo de orden 1 en z = - n para todo número natural y el cero. El residuo en cada polo es:

Valores de la función Gamma

Artículo principal: Valores de la función Gamma:

Aproximaciones

La función Gamma se puede calcular numéricamente con precisión arbitrariamente pequeña usando la fórmula de Stirling o la aproximación de Lanczos.

Para argumentos que sean múltiplos enteros de 1/24, la función Gamma puede ser evaluada rápidamente usando iteraciones de medias aritmético geométricas (véase Valores de la función Gamma).

Debido a que tanto la función Gamma como el factorial crecen muy rápidamente para argumentos moderadamente grandes, muchos programas de computación incluyen funciones que devuelven el logaritmo de la función Gamma. Este crece más lentamente, y en cálculos combinatorios es muy útil, pues se pasa de multiplicar y dividir grandes valores a sumar o restar sus logaritmos.

Aplicaciones de la función Gamma

Cálculo fraccionario:

La n-ésima derivada de axb (donde n es un número natural) se puede ver de la siguiente manera:

como n! = G(n + 1) entonces donde n puede ser cualquier número donde gamma esté definido o se pueda definir mediante límites.

De esta manera se puede calcular por ejemplo, la 1/2 derivada de x, de x2 e inclusive de una constante c = cx0:

Método de la Máxima Verosimilitud:

Existen diversos métodos para estimar los parámetros de la distribución Weibull: Basado en la relación de los parámetros con diversos percentiles de la distribución es utilizado por la simplicidad del cálculo (Bailey y Dell,1973); otro método más preciso, el de máxima verosimilitud (Zarnoch y Dell, 1995), este último ampliamente aceptado, como las derivadas parciales con respecto a los parámetros de la distribución Weibull deben ser iguales a cero en el máximo, el método selecciona a la solución de esas 2 ecuaciones como los estimados de los parámetros de la distribución Weibull. Si se contabilizan los tiempos de vida en la r-ésima falla, o no se contabilizan y entonces r=n, las ec. son:

La primera ec. se resuelve para β mediante métodos numérico. Entonces la segunda da el estimado de a. Los anteriores cálculos son fáciles en computadora, si se contabilizan los tiempos de vida en el tiempo To, se modifican los términos que tienen el factor n-r sustituyendo a cada t, por To.

Ejemplo de aplicación en el Método de la máxima Verosimilitud:

Se puede apreciar en el gráfico siguiente realizado en el programa statgraphics los parámetros de weibull (forma y escala), encontrados utilizando la función gamma con el método de la máxima verosimilitud; con la ayuda de la función gamma se puede encontrar la fiabilidad como se observa en la resolución gráfica.

Figura N°3. Gráfico de Weibull para el mes de mayo en m/s.

Fuente: Elaboración propia-2009

Así también podemos encontrar los parámetros estadísticos de la función weibull en función de a y C, para ello hay que calcular algunos valores con la función gamma.

Figura N°4. Cuadro estadístico de un año.

Fuente: Elaboración propia-2009

Software para calcular la función Gamma

Para calcular la función gamma, un programa a utilizar es Excel, con la función GAMMA.LN.

GAMMA.LN: Devuelve el logaritmo natural de la función gamma, G(x).

Sintaxis:GAMMA.LN(x)

X  es el valor cuya función GAMMA.LN se desea calcular.

GAMMA.LN se calcula como:

donde:

Para obtener la función Gamma de la función Gamma logarítmica natural:

Se escribe la fórmula: =EXP(GAMMA.LN(x)).

Ejemplo1:

=GAMMA.LN(4): Logaritmo natural de la función gamma a 4 (1,791759).

=EXP(GAMMA.LN(4)): (1,791759) es el exponente aplicado a la base e (6).

Ejemplo2:

Tabla N°1. La función gamma en función del parámetro β de la distribución Weibull.

β	G(1+1/β)	G(1+2/ β)	G(1+3/ β)	G²(1+1/ β)	s/vm
1	1	2	6	1	1
1,05	0,980792864	1,83505903	5,0291447	0,96195464	0,95269917
1,1	0,964912489	1,70242905	4,30604035	0,93105611	0,91021559
1,15	0,951701482	1,59414805	3,75395789	0,90573571	0,87181348
1,2	0,940655858	1,50457549	3,32335097	0,88483344	0,83690221
1,25	0,931383771	1,42962456	2,98120643	0,86747573	0,80500206
1,3	0,923576721	1,36627468	2,70491151	0,85299396	0,77571913
1,35	0,916989091	1,31225336	2,47859398	0,84086899	0,74872687

Conclusiones

Se ha comprobado que matemáticamente la función gamma extiende el concepto de factorial a los números complejo, haciendo excepción a los enteros negativos y ceros.

La función gamma es importante, su amplia utilización en la gran variedad de funciones de fiabilidad de dispositivos o sistemas, permite realizar mejores cálculos (ejm. Método de la máxima verosimilitud).

Bibliografía

[1] Wikipedia; Función Gamma; en: http://es.wikipedia.org/wiki/Funci%C3%B3n_gamma.

[2] LLANOS Marco; Formulario; NUEVO FORMULARIO DE CIENCIAS; Lima-Perú; Editorial: San Marcos E.I.R.L.; 2007;pg. 457.

[3] Ayuda de excel; GAMMA.LN; en: ms-help://MS.EXCEL.12.3082/EXCEL/content/HP10062507.htm

[4] TAMBORERO DEL PINO José; NTP 331: Fiabilidad: la distribución de Weibull; Centro nacional de condiciones de trabajo; España; en:www.mtas.es/insh/ntp/ntp_331.htm.

[5] PECE Martha G.; USO DE LA FUNCIÓN WEIBULL PARA MODELAR DISTRIBUCIONES DIAMÉTRICAS EN UNA PLANTACIÓN DE MELIA AZEDARACH; Santiago del Estero-Argentina; 2000; en:http:150.185.136.100/scielo.php?scrip=sci_arttext&pid=S0556-66062000000200006&Ing=es&nrm=iso&tlng=es.

[6] P. RAMÍREZ Karina;Tesis; EVALUACIÓN ENERGÉTICA COMPARATIVA DEL SISTEMA HÍBRIDO EÓLICO-FOTOVOLTAICO (SHEFV) DE BAJA POTENCIA EN EL DISTRITO DE TACNA; Tacna-Perú; 2009, pg. 160.

 

Autora:

Bach. Karina P. Ramírez

Escritora/Física/Investigadora y desarrolladora experimental en energías renovables y software.

Datos del artículo:

Fecha de realización: 11 de abril del 2009

CATEGORÍA: Tecnología

Tacna, Perú