Estadística Matemática (página 2)

Enviado por Dumar Suarez Gomez Suarez Gomez

Partes: 1, 2

Otro modo habitual, y muy útil, de
resumir una variable de tipo numérico es utilizando el
concepto de
percentiles, mediante diagramas de . La
Figura 5 muestra un gráfico de cajas
correspondiente a los datos de la

Tabla I. La caja central indica el rango en el que se
concentra el 50% central de los datos. Sus extremos son, por lo
tanto, el 1er y 3er cuartil de la distribución. La línea central en la
caja es la mediana. De este modo, si la variable es
simétrica, dicha línea se encontrará en el
centro de la caja. Los extremos de los "bigotes" que salen de la
caja son los valores
que delimitan el 95% central de los datos, aunque en ocasiones
coinciden con los valores
extremos de la distribución. Se suelen también
representar aquellas observaciones que caen fuera de este rango
(outliers o valores extremos). Esto resulta especialmente
útil para comprobar, gráficamente, posibles errores
en nuestros datos. En general, los diagramas de
cajas resultan más apropiados para representar
variables que presenten una gran desviación de la
distribución normal. Como se verá
más adelante, resultan además de gran ayuda cuando
se dispone de datos en distintos grupos de
sujetos.

Por último, y en lo que respecta a
la descripción de los datos, suele ser
necesario, para posteriores análisis, comprobar la normalidad de alguna
de las variables
numéricas de las que se dispone. Un diagrama de
cajas o un histograma son gráficos sencillos que permiten comprobar,
de un modo puramente visual, la simetría y el
"apuntamiento" de la distribución de una variable y, por
lo tanto, valorar su desviación de la normalidad. Existen
otros métodos
gráficos específicos para este propósito,
como son los gráficos P-P o Q-Q. En los primeros,
se confrontan las proporciones acumuladas de una variable con las
de una distribución normal. Si la variable seleccionada
coincide con la distribución de prueba, los puntos se
concentran en torno a una
línea recta. Los gráficos Q-Q se obtienen de modo
análogo, esta vez representando los cuantiles de
distribución de la variable respecto a los cuantiles de la
distribución normal. En la
Figura 6 se muestra el
gráfico P-P correspondientes a los datos de la
Tabla I que sugiere, al igual que el correspondiente
histograma y el diagrama de cajas, que la distribución de
la variable se aleja de la normalidad.

Comparación de
dos o más grupos

Cuando se quieren comparar las
observaciones tomadas en dos o más grupos de individuos
una vez más el método
estadístico a utilizar, así como los
gráficos apropiados para visualizar esa relación,
dependen del tipo de variables que estemos manejando.

Cuando se trabaja con dos variables
cualitativas podemos seguir empleando gráficos de
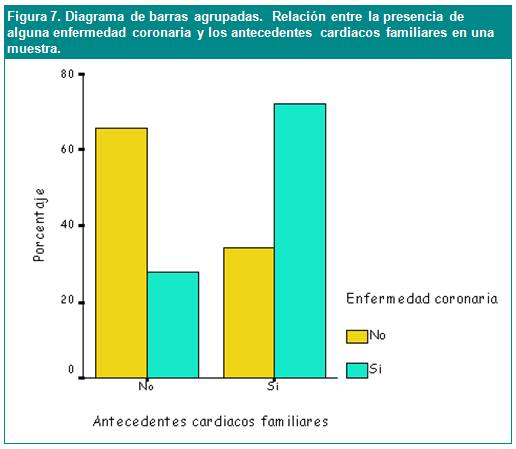
barras o de sectores. Podemos querer determinar, por ejemplo, si
en una muestra dada, la frecuencia de sujetos que padecen una
enfermedad coronaria es más frecuente en aquellos que
tienen algún familiar con antecedentes cardiacos. A partir
de dicha muestra podemos representar, como se hace en la

Figura 7, dos grupos de barras: uno para los sujetos con
antecedentes cardiacos familiares y otro para los que no tienen
este tipo de antecedentes. En cada grupo, se
dibujan dos barras representando el porcentaje de pacientes que
tienen o no alguna enfermedad coronaria. No se debe olvidar que
cuando los tamaños de las dos poblaciones son diferentes,
es conveniente utilizar las frecuencias relativas, ya que en otro
caso el gráfico podría resultar
engañoso.

Por otro lado, la comparación
de variables continuas en dos o más grupos se
realiza habitualmente en términos de su valor medio,
por medio del test t de
Student, análisis de la varianza o métodos no
paramétricos equivalentes, y así se ha de reflejar
en el tipo de gráfico utilizado. En este caso resulta muy
útil un diagrama de barras de error, como en la

Figura 8. En él se compara el índice de
masa corporal en una muestra de hombres y mujeres. Para cada
grupo, se representa su valor medio, junto con su 95% intervalo
de confianza. Conviene recordar que el hecho de que dichos
intervalos no se solapen, no implica necesariamente que la
diferencia entre ambos grupos pueda ser estadísticamente
significativa, pero sí nos puede servir para valorar la
magnitud de la misma. Así mismo, para visualizar este tipo
de asociaciones, pueden utilizarse dos diagramas de cajas, uno
para cada grupo. Estos diagramas son especialmente útiles
aquí: no sólo permiten ver si existe o no
diferencia entre los grupos, sino que además nos permiten
comprobar la normalidad y la variabilidad de cada una de las
distribuciones. No olvidemos que las hipótesis de normalidad y homocedasticidad
son condiciones necesarias para aplicar algunos de los procedimientos de
análisis paramétricos.

Por último, señalar que
también en esta situación pueden utilizarse los ya
conocidos gráficos de barras, representando aquí
como altura de cada barra el valor medio de la variable de
interés. Los gráficos de
líneas pueden resultar también especialmente
interesantes, sobre todo cuando interesa estudiar tendencias a lo
largo del tiempo
(Figura
9). No son más que una serie de puntos conectados
entre sí mediante rectas, donde cada punto puede
representar distintas cosas según lo que nos interese en
cada momento (el valor medio de una variable, porcentaje de casos
en una categoría, el valor máximo en cada grupo,
etc.).

Relación
entre dos variables numéricas

Cuando lo que interesa es estudiar la
relación entre dos variables continuas, el
método de análisis adecuado es el estudio de la
correlación. Los coeficientes de correlación
(Pearson, Spearman, etc.) valoran hasta qué punto el valor
de una de las variables aumenta o disminuye cuando crece el valor
de la otra. Cuando se dispone de todos los datos, un modo
sencillo de comprobar, gráficamente, si existe una
correlación alta, es mediante diagramas de
dispersión, donde se confronta, en el eje horizontal,
el valor de una variable y en el eje vertical el valor de la
otra. Un ejemplo sencillo de variables altamente correlacionados
es la relación entre el peso y la talla de un sujeto.
Partiendo de una muestra arbitraria, podemos construir el
diagrama de dispersión de la
Figura 10. En él puede observarse claramente como
existe una relación directa entre ambas variables, y
valorar hasta qué punto dicha relación puede
modelizarse por la ecuación de una recta. Este tipo de
gráficos son, por lo tanto, especialmente útiles en
la etapa de selección
de variables cuando se ajusta un modelo de
regresión
lineal.

Otros
gráficos

Los tipos de gráficos mostrados
hasta aquí son los más sencillos que podemos
manejar, pero ofrecen grandes posibilidades para la
representación de datos y pueden ser utilizados en
múltiples situaciones, incluso para representar los
resultados obtenidos por métodos de análisis
más complicados. Podemos utilizar, por ejemplo, dos
diagramas de líneas superpuestos para visualizar los
resultados de un análisis de la varianza con dos factores
(Figura
11). Un diagrama de dispersión es el método
adecuado para valorar el resultado de un modelo de
regresión logística (Figura
12). Existen incluso algunos análisis concretos
que están basados completamente en la
representación gráfica. En particular, la
elaboración de curvas ROC (Figura
13) y el cálculo
del área bajo la curva constituyen el método
más apropiado para valorar la exactitud de una prueba
diagnóstica.

Hemos visto, por lo tanto, como la
importancia y utilidad que las
representaciones gráficas pueden alcanzar en el proceso de
análisis de datos. La mayoría de los textos
estadísticos y
epidemiológicos4 hacen hincapié en los
distintos tipos de gráficos que se pueden crear, como una
herramienta imprescindible en la presentación de
resultados y el proceso de análisis estadístico. No
obstante, es difícil precisar cuándo es más
apropiado utilizar un gráfico que una tabla. Más
bien podremos considerarlos dos modos distintos pero
complementarios de visualizar los mismos datos. La creciente
utilización de distintos programas
informáticos hace especialmente sencillo la
obtención de las mismas. La mayoría de los paquetes
estadísticos (SPSS, STATGRAPHICS, S-PLUS, EGRET,…)
ofrecen grandes posibilidades en este sentido. Además de
los gráficos vistos, es posible elaborar otros
gráficos, incluso tridimensionales, permitiendo grandes
cambios en su apariencia y facilidad de exportación a otros programas para
presentar finalmente los resultados del estudio.