Apuntes sobre estimación de recursos y reservas (página 2)

Los principales sistemas de
clasificación que se emplean hoy en el mundo se
fundamentan en la confianza geológica y en la viabilidad
económica. Todos los esquemas de clasificación
hacen uso del grado de confiabilidad o certidumbre como factor
discriminante entre las distintas clases, entre tanto ninguno de
esos sistemas muestran claramente como calcular el error asociado
con cada estimación. Un elemento que complica aun
más el proceso de
categorización es la imposibilidad de cuantificar el error
cometido en la creación del modelo
geológico del yacimiento. Producto de
las dificultades encontradas en cuantificar el error de
estimación, los sistemas de clasificación se apoyan
más en aspectos cualitativos que en medidas reales de la
dispersión de los valores
obtenidos. Dado este elemento de subjetividad es que se introduce
en la mayoría de los sistemas de clasificación el
concepto de
persona
competente (ver código
JORC).

Los principales métodos a
través de los cuales los recursos minerales pueden
ser categorizados se dividen en 2 grupos: (1)
Criterios tradicionales o clásicos, (2) Criterios
geoestadísticos.

1.1 Métodos tradicionales de
categorización

Los métodos tradicionales de
categorización hacen uso de los siguientes
criterios.

Continuidad geológica– La
clasificación de recursos y reservas minerales depende en
primer lugar de la comprensión de la génesis del
yacimiento y de la valoración de la continuidad
geológica del volumen
mineralizado. Aquí es muy importante establecer la
continuidad física o geometría
de la mineralización o de las estructuras
controladoras. La continuidad física o geométrica
no es fácilmente cuantificable. Para establecer este tipo
de continuidad es necesario interpretar los datos disponibles
y establecer el modelo geológico del yacimiento sobre la
base del conocimiento
existente y la experiencia previa obtenida en depósitos
similares.

Densidad de la red de exploración
(grado de estudio) -Para las distintas categorías se
recomienda un determinado espaciamiento de la red de
exploración lo cual está en función
del tipo de yacimiento. Las redes para cada
categoría se argumentan sobre la base de la experiencia
(principio de analogía) en otros yacimientos similares
(tabla #1.1)

Tabla # 1.1 Ejemplo de clasificación en
función de la densidad de la
red de exploración.

Interpolación contra extrapolación
– Los bloques cuyos valores han
sido estimados por interpolación o sea están
localizados dentro de la red de muestreo son
clasificados en categorías más confiables que los
localizados más allá de la última
línea de pozos (extrapolados). La mayoría de los
sistemas de clasificación exige no incluir bloques
extrapolados en la clase de
recursos medidos.

Consideraciones tecnológicas – incluye
determinados aspectos que pueden ser utilizados para discriminar
o rechazar un recurso en una categoría dada. Como ejemplo
se pude citar la presencia de elementos perjudiciales que impiden
la buena recuperación o hacen extremadamente cara la
extracción del componente útil durante el proceso
de beneficio.

Calidad de los datos– La recuperación del
testigo, el volumen de las muestras, la forma en que fueron
tomadas y el método de
perforación influyen directamente sobre la calidad de los
datos. Los sectores donde existen problemas de
representatividad o confiabilidad de los análisis deben ser excluidos de la
categoría de recurso medido.

1.2 Criterios geoestadísticos de
categorización.

Yamamotto, 1991 considera que los esquemas de
clasificación de reservas basados en medidas reales de la
dispersión son más confiables pues reflejan, sobre
todo, la cantidad y la calidad de la información empleada para evaluar las
reservas. Estos esquemas fueron denominados genéricamente
clasificaciones geoestadísticas pues se basan en la
varianza Kriging.

En este sentido, se recomienda la Geoestadística
como procedimiento
válido y confiable en la mayoría de los sistemas de
clasificación, convirtiéndose en un estándar
en la estimación de recursos minerales.

El código propuesto por la ONU, por ejemplo,
propone el uso de la Geoestadística para clasificar los
recursos pues permite de forma rápida y sin
ambigüedad identificar las categorías de recursos y
reservas minerales(UN-ECE,1996). Algunos de los principales
criterios geoestadísticos que han sido empleados o
propuestos para la clasificación de recursos se explican a
continuación.

1.2.1 Alcance del variograma

El variograma permite cuantificar la continuidad o nivel
de correlación entre las muestras que se localizan en una
zona mineralizada dada. El grado de esa correlación ha
sido frecuentemente utilizado para clasificar los recursos y
reservas. Froidevaux (1982) propuso 3 clases de
clasificación:

Bloques en el área muestreada ubicados dentro del
radio de
influencia definido por el alcance del variograma.

Bloques en el área muestreada ubicados más
allá del radio de influencia definido por el alcance del
variograma

Bloques dentro del yacimiento ubicados a una distancia
grande de los pozos (incluyendo los bloques
extrapolados)

Típicamente se han empleado 2 enfoques para
clasificar los recursos usando el variograma

El primero se basa en la subdivisión arbitraria
del alcance observado. Ejemplo, todos los bloques estimados con
un número mínimo de muestras y ubicados dentro de
un determinado radio de influencia podrían ser
clasificados como recursos medidos mientras que todos los bloques
estimados con cierto número mínimo de muestras y
localizados más allá del radio de influencia
serían clasificados como indicados.

En el segundo enfoque las categorías de recursos
están basadas en los valores de la meseta. Por ejemplo,
los bloques comprendidos dentro de un alcance del variograma
correspondiente a 2/3 del valor de la
meseta pueden ser clasificados como medidos, el resto son
indicados.

1.2.2 Varianza Kriging

El kriging permite obtener, además de la
estimación del valor de un bloque, una indicación
de la precisión local a través de la varianza
kriging (Vk). Desde el inicio del desarrollo del
Kriging la Vk ha sido empleada para determinar los intervalos de
confianza de las estimaciones. Para esto es necesario asumir que
esta se ajusta a un modelo normal o lognormal. Sin embargo, en la
práctica es raro que los errores de estimación se
subordinen a estos modelos de
distribución.

Como para el cálculo de
la varianza kriging se emplea solamente la configuración
de las muestras en el espacio y no sus valores locales, esta no
debe ser interpretada como una medida de la variabilidad local.
Por otra parte como Vk es calculado a partir del variograma medio
del yacimiento no es solo un índice de la
disposición espacial de las muestras sino también
caracteriza las varianzas medias globales permitiendo la discriminación entre las clases o
categorías de recursos.

Este enfoque no es reciente y ha sido utilizado a lo
largo de muchas décadas, como se puede constatar en la
tabla # 1.2 que resume las categorías de la
clasificación sugerida por Diehl y David (1982) y Wellmer
(1983), basadas en la cuantificación del error utilizando
la desviación estándar kriging.

Tabla # 1.2 Clasificación de recursos/reservas
basada en la cuantificación del error a partir de la
desviación estándar kriging

El método propuesto por Diehl y David (1982) se
basa en definir niveles de confianza y de precisión
(error): la precisión se expresa en función de la
desviación estándar kriging y el valor estimado
kriging

Precisión =((kx100xZ1-()/ tki

Donde (k es la desviación estándar
kriging

tki Valor del bloque estimado por kriging

Z1-( Valor de la variable estandarizada distribuida
normalmente con un nivel de confianza (1- ()

Si se fija la precisión en 10 % (reservas
probadas) entonces se puede determinar la razón (k/ tki
que divide las reservas probadas de las probables

10==((kx100xZ80)/ tki

(k/ tki=10/(100×1.282)=0.078

Es bueno señalar que no existe consenso
internacional sobre los niveles de confianza y precisión
que deben tener las distintas categorías de
reservas.

El segundo método para categorizar los recursos
se basa en la construcción de la función de
densidad de probabilidades o el histograma de las varianzas
kriging (Annels, 1991). El histograma se examina para detectar
evidencias de
poblaciones complejas que pueden representar 3 poblaciones
superpuestas (probable, posible e inferida). Esta
situación se refleja en la figura. 1.1

Figura 1.1 Histograma de las varianzas kriging (Vk)
segmentado en 3 poblaciones: 1)0-0.0075 –Reservas
probables, 2) 0.0075-0.0135 –Reservas posibles 3)(0.0135
–Reservas inferidas (Annels, 1991)

Método del Error porcentual de la
estimación de la media

Según Valente (1982), el error porcentual de la
estimación de la media, para un conjunto den bloques estimados
para un 95 % de probabilidad
,se puede calcular por la expresión:

Donde tki y (2ki son los valores estimados por kriging y
la varianza kriging de cada uno de los bloques.

La utilización de este error para la
clasificación de recursos y reservas fue recomendado por
la ONU a las instituciones
financieras internacionales (Valente, 1982). La tabla # 1.3
representa las 3 categorías de reservas clasificadas
según el error kriging de la media para un nivel de
probabilidad del 95 %.

Tabla # 1.3 Clasificación de reservas a partir de
la utilización del error kriging de la media.

También existen otros criterios y métodos
que no serán abordados en este material como son la
simulación condicional para construir
modelos de incertidumbre, la medida de eficiencia de los
bloques (Krige,1986) y la desviación estándar de la
interpolación (Yamamoto, 1989) entre otros.

1.3 Desarrollo histórico de un sistema
internacional de clasificación de recursos y
reservas.

Desde el inicio de la década de los 90 se ha
desarrollado un esfuerzo sistemático por crear patrones
internacionales para la estimación, reporte de la
información de exploración y la
clasificación de recursos y reservas.

El código de Australasia para informar sobre
recursos minerales y reservas (código JORC) fue publicado
en Junio de 1988 e incorporado a las normas de la
bolsa de Australia. En 1990 fue publicada una guía para el
código JORC. Después de este hecho la SME (US
Society for Minig, Metallurgy, and Exploration) publicó
una guía para informar sobre datos de exploración,
recursos minerales y reservas. En 1991 en el Reino Unido el IMM
(Institute of Mining and Metallurgy) revisó sus patrones
para informar sobre recursos y reservas basándose
principalmente en el código JORC de 1988.

En septiembre de 1994 en el 15 Congreso del CMMI (Council
of Mining and Metallurgical Institutions) celebrado en
Sudáfrica, se organizó una reunión con el
objetivo
específico de discutir los estándar
internacionales, esto resultó ser el primer encuentro de
lo que posteriormente fue llamado el Grupo CMMI
(International Resource/reserve definitions group).

El Grupo CMMI, compuesto por representantes de Australia
(AusIMM), África del
Sur (SAIMM), Estados Unidos (
SME), Reino Unido (IMM) y Canadá (CIM), tenía como
objetivo desarrollar un conjunto de definiciones internacionales
relacionadas con los recursos minerales y las reservas de
mena.

De la misma forma en 1992 las Naciones Unidas
creó una comisión para desarrollar un sistema
internacional de clasificación de recursos y reservas, el
cual salió a la luz en 1996 bajo
el nombre de Marco Internacional de las Naciones Unidas para la
clasificación de reservas/recursos – Combustibles
sólidos y sustancias minerales ("United Nations
International Framework Classification for reserve /
resource-Solid fuels and mineral Commodity ").

El primer gran avance ocurrió en octubre de 1997
en el encuentro del grupo CMMI en Denver Colorado y la
aprobación del llamado acuerdo de Denver donde se
logró un consenso sobre un conjunto de definiciones de
recursos y reservas. En 1998 en Ginebra, Suiza se llevo a cabo un
encuentro entre el grupo CMMI y la comisión de Naciones
Unidas, donde las definiciones y patrones del CMMI fueron
incorporados, con pequeñas modificaciones, al sistema de
clasificación de las Naciones Unidas, dándole un
carácter verdaderamente internacional a las
definiciones del CMMI.

Después de encuentro Australia, África del
Sur y Estados Unidos iniciaron la actualización de sus
sistemas nacionales de clasificación

En noviembre de 1999 hubo un nuevo encuentro entre el
Grupo CMMI y la comisión de Naciones Unidas para continuar
el proceso de desarrollo de normas y definiciones
internacionales. Con pequeñas e insignificantes
diferencias entre los países los siguientes
términos han sido aceptados (fig. 1.2):

Recursos minerales es una
concentración u ocurrencia de material de interés
económico intrínseco en o sobre la corteza de
la Tierra en
forma y cantidad en que haya probabilidades razonables de una
eventual extracción económica. La
ubicación, cantidad, ley,
características geológicas y continuidad de un
Recurso Mineral son conocidas, estimadas o interpretadas a partir
de evidencias y conocimientos geológicos
específicos. Los Recursos Minerales se subdividen, en
orden ascendente de la confianza geológica, en
categorías de Inferidos, Indicados y
Medidos.

Figura 1.2 Relación general entre Resultados de
Exploración, Recursos y Reservas Minerales

Recurso Mineral Inferido es aquella
parte de un Recurso Mineral por la cual se puede estimar el
tonelaje, ley y contenido de mineral con un bajo nivel de
confianza. Se infiere a partir de evidencia geológica y se
asume pero no se certifica la continuidad geológica ni de
la ley. Se basa en información inferida mediante técnicas
apropiadas de localizaciones como pueden ser afloramientos,
zanjas, rajos, laboreos y sondajes que pueden ser limitados o de
calidad y confiabilidad incierta.

Recurso Mineral Indicado es aquella
parte de un Recurso Mineral para el cual puede estimarse con un
nivel razonable de confianza el tonelaje, densidad, forma,
características físicas, ley y contenido mineral.
Se basa en información sobre exploración, muestreo
y pruebas
reunidas mediante técnicas apropiadas en ubicaciones como
pueden ser: afloramientos, zanjas, rajos, túneles,
laboreos y sondajes. Las ubicaciones están demasiado
espaciadas o su espaciamiento es inapropiado para confirmar la
continuidad geológica y/o de ley, pero está
espaciada con suficiente cercanía para que se pueda
suponer continuidad.

Recurso Mineral Medido es aquella
parte de un Recurso Mineral para el cual puede estimarse con un
alto nivel de confianza el tonelaje, su densidad, forma,
características físicas, ley y contenido de
mineral. Se basa en la exploración detallada
einformación confiable sobre muestreo y pruebas obtenidas
mediante técnicas apropiadas de lugares como pueden ser
afloramientos, zanjas, rajos, túneles, laboreos y
sondajes. Las ubicaciones están espaciadas con suficiente
cercanía para confirmar continuidad geológica y/o
de la ley.

Reserva Minerales es la parte
económicamente explotable de un Recurso Mineral Medido o
Indicado. Incluye dilución de materiales y
tolerancias por pérdidas que se puedan producir cuando se
extraiga el material. Se han realizado las evaluaciones
apropiadas, que pueden incluir estudios de factibilidad e
incluyen la consideración de modificaciones por factores
razonablemente asumidos de extracción,
metalúrgicos, económicos, de mercados,
legales, ambientales, sociales y gubernamentales. Estas
evaluaciones demuestran en la fecha en que se reporta que
podría justificarse razonablemente la extracción.
Las Reservas de Mena se subdividen en orden creciente de
confianza en Reservas Probables Minerales y Reservas Probadas
Minerales

Reserva Probable Minerales es la
parte económicamente explotable de un Recurso Mineral
Indicado y en algunas circunstancias Recurso Mineral Medido.
Incluye los materiales de dilución y tolerancias por
pérdidas que puedan producirse cuando se explota el
material. Se han realizado evaluaciones apropiadas, que pueden
incluir estudios de factibilidad, e incluyen la
consideración de factores modificadores razonablemente
asumidos de minería,
metalúrgicos, económicos, de mercadeo,
legales, medioambientales, sociales y gubernamentales. Estas
evaluaciones demuestran a la fecha en que se presenta el informe, que la
extracción podría justificarse
razonablemente

Reserva Probada Minerales es la
parte económicamente explotable de un Recurso Mineral
Medido. Incluye los materiales de dilución y tolerancias
por pérdidas que se pueden producir cuando se explota el
material. Se han realizado evaluaciones apropiadas que pueden
incluir estudios de factibilidad, e incluyen la
consideración de modificaciones por factores
fehacientemente asumidos de minería, metalúrgicos,
económicos, de mercados, legales, ambientales, sociales y
gubernamentales. Estas evaluaciones demuestran, a la fecha en que
se publica el informe, que la extracción podría
justificarse razonablemente.

Con esos términos y definiciones aceptadas, el
grupo CMMI se dedicó a desarrollar las normas
internacionales. La responsabilidad por las estimaciones de recursos y
reservas debe ser atribuida a una persona responsable/competente,
término este introducido inicialmente en el código
JORC.

Con el establecimiento y adopción
de los patrones internacionales de estimación y
clasificación de recursos y reservas muchos autores
discuten la perspectiva inminente de transformar esos patrones en
normas de certificación del sistema ISO 9001.
Según Vallee, 1999 de todos los sistemas en uso el
código JORC es el más compatible con la
certificación ISO.

Métodos
clásicos de estimación de reservas

Estos métodos sencillos, que se basan en
criterios meramente geométricos, han soportado el paso del
tiempo. Sin
embargo están siendo paulatinamente sustituidos por
métodos más sofisticados de estimación que
se basan en la aplicación de los métodos de
estimación espacial.

2.1 Parámetros básicos de la
estimación de recursos.

Los principales parámetros de estimación
se deducen del la ecuación básica que permite
calcular la cantidad de metal o componente útil
(P).

P = S*m*d*C donde,

S- área de la proyección del cuerpo
mineral en un plano determinado.

m- potencia media
del cuerpo mineral en la dirección perpendicular al plano de
proyección

d- masa volumétrica

C- ley media del componente útil.

De esta ecuación básica se pueden derivar
otras fórmulas como:

V=S*m – volumen total ocupado por el yacimiento
mineral (m3)

Q=V*d – Tonelaje o cantidad de reservas de mineral
útil (t)

La fórmula anterior muestra que los
principales parámetros son:

A) área (m2)

B) espesor medio (m)

C) contenido medio de los componentes útiles (%,
g/t, g/m3, kg/m3)

D) Masa volumétrica o densidad aparente de la
materia prima
mineral (t/m3)

Antes de comenzar el cálculo es necesario
determinar los valores de esos parámetros a partir de los
datos adquiridos en el transcurso de los trabajos de
prospección y exploración. Esta tarea es muy
importante pues de su correcta solución depende la
precisión de los resultados de la
estimación

2.2 Determinación de los parámetros
básicos

2.2.1 Determinación del área del
yacimiento

Después del levantamiento geológico y la
documentación de los trabajos de
exploración se puede representar el yacimiento
proyectándolo en un plano conveniente. Habitualmente los
yacimientos con un buzamiento mayor de 45º se proyectan en
un plano vertical, los de buzamiento menor se proyectan en un
plano horizontal. En ambos casos el área proyectada es
menor que el área real. La relación entre el
área real (S) y el área proyectada (S´) en el
plano vertical es:

S´=S*sen (ÃY)

Para el plano horizontal:

S´=S*cos (ÃY)

Donde ÃY es el ángulo de buzamiento del
yacimiento.

Los yacimientos que tienen un rumbo y buzamiento
constantes pueden ser proyectados en un plano paralelo a los
mismos. Si el depósito está constituido por varios
cuerpos el área de cada uno se proyecta y determina
aparte.

La base para la proyección de los cuerpos y el
cálculo del área son los planos del departamento
del servicio
topográfico. En estos planos el geólogo debe
delimitar el área del cuerpo estudiado, demarcar los tipos
tecnológicos y las categorías según el grado
de estudio etc.

Para calcular el área es necesario inicialmente
determinar los contornos de los cuerpos y del yacimiento mineral.
Comúnmente se trazan dos contornos o límites:
el interno y el externo. El contorno interno es una línea
que une todos los pozos externos positivos. Ahora bien como el
cuerpo mineral continua mas allá del contorno interno y no
es posible conocer la posición exacta del contorno real se
hace necesario determinar un límite (contorno externo) que
sustituye el contorno real.

Pueden existir 2 posibilidades:

Detrás de los pozos extremos positivos se
encuentra un pozo estéril

Detrás de los pozos extremos positivos no existen
pozos de exploración

En el primer caso sabemos que el contorno real se
encuentra en alguna parte entre el contorno interno y los pozos
negativos entonces el contorno externo se determina por
extrapolación limitada. En el segundo caso no existen
datos sobre la posición exacta del contorno real y este se
determina por extrapolación no limitada. Los distintos
métodos que existen para determinar el contorno externo se
representan en la figura 2.1.

Figura 2.1 Principales criterios para trazar el contorno
externo

Una vez contorneado el yacimiento el área puede
ser calculada empleando una de los siguientes
métodos:

Planímetro

Digitalizador

Descomposición en figuras geométricas
sencillas.

Papel milimetrado

Regla de Simpson

2.2.2 Determinación de la masa
volumétrica

La masa volumétrica de la mena (o mineral) no es
más que la masa de un metro cúbico de esta en
estado
natural, es decir incluyendo poros, cavidades etc.

La masa volumétrica (d) de la mena se define
como:

d= Q/(Vm+Vp)

donde: Q es la masa de la muestra de mena

Vm es el volumen de la mena

Vp es el volumen de los poros

La masa volumétrica se puede calcular en el
laboratorio,
en el campo y por métodos geofísicos principalmente
en pozos y excavaciones mineras. En el laboratorio se determina
mediante el pesaje de las muestras y la determinación del
volumen. La medición más exacta y
auténtica se logra en el campo para esto se extrae una
muestra global (alrededor de 10 m3). El volumen del espacio (V)
se mide y la mena extraída se pesa (Q).

d= Q/V (t/m3)

La masa volumétrica de la mena puede cambiar en
función de la composición química y
eventualmente de la textura, esto determina la necesidad de
determinar la masa volumétrica para cada tipo natural de
mena presente en el yacimiento. Habitualmente el peso
volumétrico se determina para cada tipo como un promedio
aritmético de 10 –20 muestras, en caso de
yacimientos complejos de 20- 30 muestras

La selección
de una insuficiente cantidad de muestras y la no
representatividad de las mismas constituyen las fuentes
principales de errores en la determinación de la masa
volumétrica.

Muchas minas en operaciones
aplican una masa volumétrica constante (t/m3), la cual se
obtiene a partir del promedio aritmético de un
número significativo de muestras. Si embargo esto puede
conducir a errores graves en la determinación del tonelaje
y la cantidad de metal, especialmente en aquellos casos donde la
ley, la litología de la roca de caja, el grado de
alteración o la profundidad del intemperismo y la
mineralogía del componente útil varían
constantemente.

Para superar este problema se emplea la regresión
lineal. Este método consiste en la
determinación de la masa volumétrica de un
número significativo de muestras mineralizadas
pertenecientes a un mismo tipo natural de mena.
Simultáneamente las muestras son analizadas para conocer
el contenido del componente útil. Con esta
información se construye el gráfico de
dispersión, se realiza el análisis de
correlación y se ajusta la ecuación de
regresión que permite predecir el valor de la masa
volumétrica de cada muestra en función de la ley
del componente útil. Sobre la base de estos resultados
también se confeccionan los nomogramas que permiten
obtener directamente el valor de la masa volumétrica a
partir de la ley del componente útil de la muestra o
intersección.

2.2.3 Determinación del espesor medio de un
yacimiento

El espesor de un yacimiento se puede verificar por
métodos directos o con ayuda de modos indirectos (por
ejemplo los métodos geofísicos en las
perforaciones)

El espesor o potencia se puede medir en los
afloramientos naturales y artificiales, en las excavaciones
mineras y en los pozos de perforación.

El espesor de los yacimientos hay que medirlo con una
precisión de cm. En casos de yacimientos con contactos
claros con las rocas vecinas el
espesor se mide directamente. Cuando los contornos de la mineral
no son claros el espesor se determina sobre la base de los
resultados de los análisis químicos de las muestras
y la precisión depende de la longitud de las muestras
tomadas. .

En la estimación de recursos se puede emplear la
potencia real o normal, la componente vertical (potencia
vertical) y la componente horizontal (potencia horizontal). Todo
depende del plano en el cual se ha proyectado el cuerpo. La
dependencia entre el espesor real y los espesores horizontales y
verticales es la siguiente.

mn = mh* sen (ÃY)

mn = mv * cos(ÃY)

mh = mv * ctg (ÃY)

Donde ÃY es el ángulo de buzamiento de
cuerpo, mn-potencia real mh – potencia horizontal, mv –
potencia vertical.

La componente vertical se emplea cuando el yacimiento se
proyecta en planos horizontales principalmente para los cuerpos
de buzamiento suave. Como se observa en la figura 2.2 trabajar
con la componente vertical y el área proyectada en el
plano horizontal es equivalente a emplear la potencia real y el
área real de cuerpo mineral.

Figura 2.2 Empleo de la
potencia vertical cuando se proyecta el cuerpo en el plano
horizontal. (Annels, 1991).

La componente horizontal se emplea cuando los cuerpos se
representan en proyecciones verticales longitudinales
principalmente en cuerpos de yacencia abrupta que se explotan con
minería subterránea.

La potencia aparente del cuerpo mineral es de poca
importancia y su valor depende del buzamiento y la
inclinación del pozo. Si se conoce el ángulo de
intersección (?) entre el cuerpo mineral y el eje (traza
del pozo) o puede medirse en el testigo entonces es posible
calcular la potencia real empleando la siguiente
fórmula.

mn = ma* sen (?)

En caso de que el ángulo de intersección
no pueda ser medido, el espesor real se calcula a partir de la
inclinación del pozo (a) en el punto medio del intervalo
mineralizado y el buzamiento del cuerpo (ÃY) determinado a
partir del perfil.

mn = ma* sen (a+ ÃY)

En los casos en que el plano vertical que contiene el
pozo no es perpendicular al rumbo del cuerpo mineral entonces es
necesario introducir un factor de corrección (Rm) en la
fórmula anterior

mn = ma* sen (a+ ÃY)*Rm

Rm= sen (a+ d)*cos(ÃY)/cos(d)

Donde d es el buzamiento aparente del cuerpo mineral en
el plano vertical que contiene el pozo.

También se puede emplear la
fórmula

mn = ma* sen (a+ ÃY)*cos(?)

Siendo ? el ángulo entre el plano vertical que
contiene el pozo y un plano vertical perpendicular al rumbo del
cuerpo mineral.

Para la estimación de reservas es necesario
determinar el espesor medio del yacimiento o de una parte de
este. Si los espesores particulares fueron medidos a distancias
regulares, el espesor medio se calcula según la
fórmula de la media aritmética.

m = (m1+m2+m3+··· +mn)/n

Si las mediciones de los espesores de un yacimiento
fueron realizadas en distancias no regulares entonces el espesor
medio se calcula según la ecuación de la media
ponderada, empleando como factor de ponderación las
distancias entre las distintas mediciones (l) o el área de
influencia de cada una de ellas.

m = (m1ll+m2l2+m3l3+ ··
+mnln)/(l1+l2+l3+····+ ln)

2.2.4 Determinación del contenido medio del
componente útil

Durante la exploración de un yacimiento se
muestrean de forma continua los distintos tipos de mena. Los
análisis de las muestras permiten conocer el contenido o
ley del componente útil en los lugares donde las muestras
fueron tomadas.

El contenido de un componente útil en la mena en
la mayor parte de los casos se expresa en % de peso (Ej. Fe, Mn,
Cu, Pb, Sb, Hg etc), sin embargo los metales preciosos
(Au, Ag, Pt etc.) se indican en gramos por tonelada (g/t).
Finalmente en los yacimientos de placeres la ley de los metales
se expresa en g/m3 o Kg/m3.

Durante la exploración, las concentraciones de
los componentes útiles se determinan a través de
muestras individuales es por esto que la estimación de los
contenidos promedios para cada bloque se realiza en 2
etapas:

• Cálculo del contenido promedio del componente
  útil en cada pozo o intersección de
  exploración a lo largo de toda la potencia del cuerpo
  mineral.

• Extensión de los contenidos determinados en
  las intersecciones a los volúmenes adyacentes del
  subsuelo.

Antes de comenzar la primera etapa es necesario
determinar en cada pozo cual es el intervalo que puede ser
explotado con cierto beneficio económico. Para este fin se
emplean las condiciones industriales: potencia mínima
industrial, contenido mínimo industrial, contenido en los
bordes etc.

Para obtener la ley media de cada pozo siempre se emplea
el método de la media ponderada empleando como factor de
peso las longitudes de cada muestra individual. En caso de que la
longitud de las muestras sea constante entonces se utiliza la
media aritmética.

Ci- Ley de cada muestra individual

li – Longitud de cada muestra

C- Ley media de la intersección
económica

La extensión de los contenidos medios
calculados para cada pozo o intersección a los
volúmenes adyacentes del subsuelo se hace frecuentemente
por vía estadística. Con este fin en los
métodos clásicos de cálculo se emplea tanto
la media aritmética como la media ponderada. En el caso de
los métodos asistido por computadoras
la extensión de los contenidos se realiza empleando
métodos de interpolación espacial como el kriging y
el inverso de la distancia, los cuales serán abordados en
próximos capítulos.

2.3 Consideraciones generales sobre la
estimación de recursos

Matemáticamente la estimación de recursos
no es más que la integración numérica de una
función contenido o ley (expresada en unidades de masa por
unidad de volumen) dentro del yacimiento de volumen V.

La figura 2.3a muestra el procedimiento de
cálculo de reservas a partir de la integración de
la función ley C(v) en el dominio
V.

a) b)

Figura 2.3 Yacimiento mineral hipotético cuya
función contenido C(v) es conocida y por tanto la reserva
de metal se calcula por su integración numérica en
el dominio del yacimiento .b) yacimiento subdividido en bloques
de volúmenes conocidos y las leyes
determinadas por un método de
estimación.

Conocer la función C(v) implica saber en cada
punto del yacimiento cual es la ley del componente útil o
sea la función que la describe matemáticamente. En
la práctica esto es imposible dada la densidad del
muestreo por un lado y por otra parte la incapacidad de encontrar
una función que se ajuste perfectamente a los
datos.

Como no se puede resolver directamente la
ecuación los métodos existentes de
estimación de reservas, tanto los tradicionales como los
asistidos por computadoras, solucionan la ecuación
empleando el caso discreto.

Donde Ci – ley del componente en el bloque i

Vi – volumen del bloque i

V- Volumen total del yacimiento

La ecuación anterior se resuelve
fácilmente subdividiendo el yacimiento en n bloques de
volúmenes conocidos, cuyas leyes pueden ser determinadas
por los métodos de cálculo existentes como se
ilustra en la figura 2.3b.

La estimación de recursos es siempre hecha en
bloques cuya geometría se define por la
localización de los trabajos de exploración en el
caso de los métodos clásicos, o en bloques de
cálculo definidos por la malla o red en el caso de los
métodos computacionales. Es justamente aquí donde
radica la diferencia fundamental entre los métodos
clásicos y los asistidos por computadoras ya que los
primeros determinan las reservas en bloques de cálculos de
grandes dimensiones y los segundos en bloques de pequeñas
dimensiones compatibles con la densidad de
información.

2.4 Métodos clásicos de
estimación de reservas

Los métodos clásicos, desarrollados y
empleados desde los mismos comienzos de la minería, se
basan fundamentalmente en los principios de
interpretación de las variables
entre dos puntos contiguos de muestreo, lo que determina la
construcción de los bloques geométricos a los que
se le asignan las leyes medias para la estimación de
recursos.

Los principios de interpretación de estos
métodos según Popoff (1966) son los
siguientes:

Principio de los cambios graduales (función
lineal) entre dos puntos de muestreo

Principio de los vecinos más cercanos o zonas de
influencia

Principio de generalización (analogía) o
inferencia geológica.

El principio de los cambios graduales presupone que los
valores de una variable (espesor, ley, etc.) varían
gradual y continuamente a lo largo de la línea recta que
une 2 puntos de muestreo contiguos.

El principio de vecinos más cercanos admite que
el valor de la variable de interés en un punto no
muestreado es igual al valor de la variable en el punto
más próximo.

El último de los principios permite la
extrapolación de los valores conocidos en los puntos de
muestreo a puntos o zonas alejadas sobre la base del conocimiento
geológico o por analogía con yacimientos
similares.

Todos estos principios de interpretación son
utilizados para la subdivisión del yacimiento mineral en
bloques o sectores, los cuales son evaluados individualmente y
posteriormente integrados para determinar los recursos totales
del yacimiento.

Los métodos clásicos o tradicionales han
soportado el paso del tiempo pero están siendo superados
progresivamente por los métodos geoestadísticos.
Estos métodos son aun aplicables en muchas situaciones,
donde incluso pueden arrojar resultados superiores. Siempre es
necesario realizar una valoración crítica
del empleo de la geoestadistica antes de desechar completamente
las técnicas tradicionales. El uso de las técnicas
kriging está supeditado a la existencia de una red de
exploración que permita la generación de los
modelos matemáticos que describen la continuidad
espacial de la mineralización del yacimiento que se
evalúa. Cuando no existe suficiente información de
exploración o la variabilidad es extrema se deben emplear
los métodos geométricos o tradicionales.

Según Lepin y Ariosa, 1986 los métodos
clásicos de estimación más conocidos
son:

Método del promedio aritmético o bloques
análogos

Método de los bloques
geológicos

Método de los bloques de
explotación

Método de los polígonos

Método de las isolíneas.

Método de los perfiles

2.4.1 Método de la media
aritmética.

Es el método de cálculo más simple.
En este caso la forma compleja del cuerpo mineral se sustituye
por una placa o lámina de volumen equivalente cuyo espesor
corresponde con la potencia media del cuerpo.

Los contornos se trazan en los planos o proyecciones
verticales. El área delimitada se determina
planimétricamente o por otro método de
cálculo. El espesor medio se estima por la media
aritmética simple o ponderada. El contenido promedio y la
masa volumétrica se determina de la misma forma. La parte
del cuerpo comprendida entre el contorno interno y externo
generalmente se calcula de manera independiente porque los
recursos de esta zona se reportan en una categoría
inferior. A pesar de su sencillez se puede emplear exitosamente
en yacimientos de constitución geológica simple Ej.
Yacimientos de materiales de la construcción.

Secuencia General de trabajo.

-Delimitación del área del cuerpo mineral,
trazando el contorno interno y externo.

-Medición del área

-Cálculo de la potencia media del mineral
útil por promedio aritmético o media
ponderada.

-Cálculo de la masa volumétrica por
promedio aritmético o media ponderada.

-Cálculo de la ley media del mineral útil
por promedio aritmético o media ponderada.

-Cálculo del volumen, tonelaje (reservas de mena)
y reservas del componente útil.

Ventaja

Su principal mérito radica en su simplicidad,
brindando una rápida idea sobre los recursos de un
yacimiento. Se utiliza en los estadios iniciales de los trabajos
geológicos de exploración para realizar
evaluaciones preliminares.

Desventaja

Imposibilidad del cálculo selectivo de acuerdo
con las diferentes clases industriales de mena, condiciones de
yacencia, grado de estudio y condiciones de
explotación.

2.4.2 Método de los bloques
geológicos

El cuerpo mineral se divide en bloques homogéneos
de acuerdo a consideraciones esencialmente geológicas. De
esta forma el cuerpo mineral de morfología
compleja se sustituye por un sistema de prismas
poliédricos de altura que corresponde con la potencia
media dentro de cada bloque (fig2.4). El contorneo se realiza en
cualquier proyección del cuerpo, además es
necesario trazar los límites de los bloques
geológicos independientes.

Figura 2.4 Estimación de reservas por el
método de bloques geológicos

Generalmente se forman bloques tomando en
consideración la variación de los siguientes
parámetros:

Según las diferentes vetas, capas o cuerpos
presentes en el yacimiento

Según la existencia de intercalaciones
estériles

Según la potencia del cuerpo mineral

Según la profundidad o cota de nivel

Según los tipos tecnológicos, calidad o
contenido de componente útil (mena rica y mena
pobre)

Según las condiciones hidrogeológica (por
encima y por debajo del nivel freático)

Según el coeficiente de destape o relación
estéril mineral.

Según la situación
tectónica

Además de estos criterios geológicos se
consideran otros aspectos como:

Diferencias en el grado de conocimiento

Viabilidad económica.

Es importante señalar que si se toman en
consideración muchos parámetros el resultado
será la formación de muchos bloques. En caso
extremo cada pozo representa un bloque separado lo que reduce el
método de bloques geológico al método de los
polígonos.

Este método se reduce al anteriormente descrito
si se delimita un solo bloque que abarque todo el yacimiento. La
metodología de cálculo dentro de
cada bloque es exactamente igual al método de media
aritmética. Las reservas totales del yacimiento se
obtienen de la sumatoria de las reservas de los bloques
individuales.

El método, que se caracteriza por su sencillez en
el contorneo y el cálculo, puede ser aplicado
prácticamente para cuerpos minerales de cualquier
morfología, explorados según una red regular o
irregular y cualquiera que sean las condiciones de
yacencia.

El problema fundamental de esta técnica radica en
que durante el desarrollo y explotación del yacimiento, es
necesario reajustar todos los bloques para que se acomoden al
método de explotación.

2.4.3 Método de los bloques de
explotación

Este método es también una variante del
método de la media aritmética y se
desarrolló esencialmente para los yacimientos filoneanos,
los cuales son divididos en bloques por los laboreos de
preparación para la explotación.

Según este método, específico de la
minería subterránea, las reservas del yacimiento se
calculan por la acumulación de las reservas parciales
obtenidas en bloques de explotación individuales. Los
bloques de cálculo son porciones del depósito
delimitadas por 2, 3 y 4 lados por excavaciones mineras de
exploración y desarrollo (contrapozos, corta vetas,
galerías, trincheras etc.).

La forma real del cuerpo dentro del bloque se reemplaza
con un paralelepipedo cuya altura es igual a la potencia media
del cuerpo mineral en el bloque.

El cálculo se realiza en el plano o en la
proyección vertical longitudinal, sobre los cuales se
proyectan las excavaciones mineras con los resultados de los
análisis y los espesores particulares.

Para el cálculo de la potencia y el contenido
medio dentro de cada bloque, primeramente se determinan los
valores medios en cada excavación y posteriormente se
calcula el valor medio del bloque a través de la media
aritmética si la longitud de la excavaciones son
aproximadamente iguales, en caso contrario se pondera por la
longitud o área de influencia de cada laboreo.

La ventaja del método radica en la sencillez del
contorneo y la posibilidad de usar los resultados directamente en
la proyección y planificación de la extracción del
mineral útil. Su debilidad principal radica en la
división formal del cuerpo en bloques heterogéneos
por la potencia y calidad.

2.4.4 Método de los polígonos o
regiones próximas

El método se emplea para el cálculo de
reservas de capas horizontales o subhorizontales explorados por
pozos irregularmente distribuidos.

Si se calculan las reservas de un depósito
según este método la morfología compleja del
yacimiento se reemplaza por un sistema de prismas
poliédricos, cuyas bases lo constituyen los
polígonos o zonas de influencia y su altura es igual al
espesor del cuerpo revelado por el pozo que se ubica en el centro
del polígono.

El método se reduce a la separación de las
zonas de influencia de cada pozo o laboreo que intercepta el
cuerpo mineral. Para la delimitación de las zonas de
influencia es necesario realizar las siguientes
construcciones:

Se procede a unir mediante líneas rectas los
pozos de perforación contiguos posteriormente se determina
la mediatriz de cada recta y la intersección de las mismas
definen la zona de influencia. Este procedimiento, que se conoce
como división de Dirichlet o poligonos de Voronoi
(Thiesen), genera un sistema único de prismas
poliédricos en el cual los polígonos contiguos
comparten una arista común (Fig. 2.5). El empleo de este
procedimiento permite obtener siempre el mismo mosaico de
polígonos.

Figura 2.5 Estimación de reservas por el
método de los polígonos. a) Parte de un plano de
cálculo indicando la forma en que se construyen los
polígonos a partir de un pozo 1)Pozo positivo 2)Pozo
negativo 3)limite de los polígonos de cálculo
4)Contorno interno 5)contorno externo (Kreiter, 1968)

El volumen del prisma se determina como el producto del
área del polígono por su altura. Otros
parámetros del cálculo se obtienen para cada prisma
directamente del pozo central. El volumen total del yacimiento es
la suma de los volúmenes de cada prismas.

Este método puede ser utilizado para estimaciones
preliminares de recursos, pues los cálculos son tan
simples que pueden ser hechos rápidamente incluso en el
campo, otra ventaja importante del método es su
reproducibilidad pues si se sigue el mismo procedimiento dos
especialistas pueden llegar al mismo resultado.

El método de los polígonos posee muchas
desventajas entre las que podemos mencionar:

Cuando la red de exploración es densificada, hay
que rehacer nuevamente la construcción de los
polígonos.

El sistema de los prismas no refleja correctamente la
forma natural del yacimiento.

Los resultados no son satisfactorios principalmente
cuando los valores observados son valores extremos lo cual
provoca que los errores de extensión del pozo al
polígono sean muy groseros. Este error de
estimación disminuye en la medida que aumenta la densidad
de la red de exploración

Independientemente de las desventajas obvias que posee
el método, las cuales están muy vinculadas con su
sencillez y simplicidad, esta técnica de estimación
ha soportado el paso del tiempo y aparece implementado en la
mayoría de los softwares modernos de modelación
geólogo minera.

2.4.5 Método de las
isolíneas

La estimación de recursos por el método de
las isolíneas presupone que los valores de la variable de
interés varían gradual y continuamente entre las
intersecciones de exploración

Durante la estimación de las reservas de un
yacimiento por este método, la forma de este se sustituye
por un cuerpo de volumen igual al cuerpo natural, pero delimitado
en su base por un plano recto (fig2.6). En este método se
comienza con el trazado de los mapas de
isolíneas de las variables de interés (espesor, ley
y masa volumétrica o reservas lineales). Las
isolíneas entre los laboreos de exploración se
construyen empleando el método de triangulación con
interpolación lineal.

Figura 2.6 Esquema de estimación de recursos
empleando el método de las isolíneas. Plano de
isopacas con malla superpuesta y algunos pozos de
exploración a)Forma transformada del cuerpo mineral en un
perfil geológico b)Forma real del cuerpo; ?S área
elemental de la celda con altura 2.9 m y volumen elemental
V=100*2.9=290 m3,Si–área dentro de la
isolínea, h – equidistancia ente isolíneas, hx
–altura o profundidad de las cúpulas

El volumen del cuerpo representado por las
isolíneas de espesor (isopacas) se puede calcular por el
método de la red milimétrica.

En esta variante es necesario trazar los mapas de
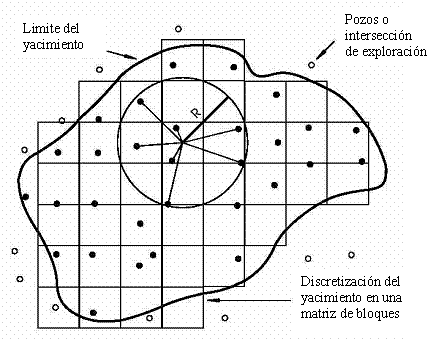
isovalores del espesor, ley de los componentes útiles y
masa volumétrica. Posteriormente se superpone una malla o
matriz de
bloques, cuyo tamaño está en correspondencia con la
escala de los
trabajos y la densidad de la red de exploración. La matriz
divide toda el área del yacimiento en pequeños
bloques cuadrados. Posteriormente a partir del mapa de isopacas
se interpola el valor de la potencia en el centro de cada bloque
lo cual permite determinar el volumen de cada celda elemental.
Por la adición de estos volúmenes elementales (?V)
se determina el volumen total del yacimiento. Si se considera
necesario para mejorar la precisión en los bloques
limítrofes, se puede estimar la proporción del
bloque que se localiza dentro de los contornos del
yacimiento.

?V=?S*mi

Donde ?V –volumen elemental de la celda o
bloque

mi –
espesor del yacimiento en el centro del área parcial, se
determina por interpolación

?s –área de la celda (valor
constante)

El volumen total del cuerpo se calcula:

De esta expresión queda claro que el volumen de
un yacimiento se determina como el producto del área
elemental del bloque con la suma de los espesores parciales que
se determinan por interpolación lineal a partir de las
isolíneas.

El cálculo de las reservas de menas del
yacimiento es exactamente igual si la masa volumétrica es
variable se construye el mapa de isovalores de este
parámetro y a partir de aquí se interpola el valor
"d" en cada celda.

Si d es constante entonces la formula queda de la
siguiente forma

De forma análoga se estima la cantidad de
metal

Esta variante del método de isolíneas es
extremadamente importante pues contienen en esencia la idea
fundamental sobre la que descansan los métodos modernos
asistidos por computadoras. En ellos también se subdivide
o discretiza el yacimiento en pequeños bloques y
posteriormente se estima en cada celda el valor de la variable de
interés, con la única diferencia que en los
métodos actuales la interpolación se basa en
métodos de estimación espacial
(geoestadísticos y geomatemáticos). La
comprensión de esta variante es fundamental para poder entender
los métodos que serán discutidos en los
próximos capítulos.

En resumen se puede decir que una de las ventajas del
método de isolíneas es su claridad pues las curvas
de isovalores brindan una idea clara sobre la constitución
del yacimiento y el comportamiento
de los espesores y contenidos del componente útil. Para
trazar las isopacas no es necesario emplear espesores reales sino
que se puede usar la componente vertical u horizontal de la
potencia, todo depende del plano en el que se proyecte el cuerpo.
El método permite realizar estimaciones locales (bloque a
bloque) lo cual facilita la utilización de los resultados
para fines de planificación minera.

Según la literatura la principal
desventaja del método radica en la complicación de
las construcciones, la cual ha sido superada con la introducción de los ordenadores y el
desarrollo de los métodos geoestadísticos. El
principal problema del método está en la necesidad
de contar con un grado de exploración alto pues la
construcción de las isolíneas sobre la base de una
red de exploración poco densa no es confiable.

2.4.6 Métodos de los perfiles

El método de estimación mediante cortes o
perfiles se puede usar si el yacimiento fue explorado en una red
regular que permite la construcción de cortes
geológicos. Los cortes geológicos de un yacimiento,
según su orientación, pueden ser horizontales,
verticales o perfiles no paralelos. La distancia ente los cortes
particulares no es constante y corresponde a la distancia entre
las líneas de exploración en el caso de perfiles
verticales o la altura entre niveles de una mina en el caso de
cortes horizontales.

Figura 2.7 Cálculo de recursos usando el
método de perfiles paralelos. Para simplificar el esquema
solo se trazó el contorno externo. 1-Pozos positivos y
negativos 2-número de los perfiles geológicos
3-número de los bloques de cálculo
4-intercalación de roca estéril, S – área
del cuerpo en los perfiles L- distancia entre los
perfiles

La sucesión de cálculo en este caso es la
siguiente.

• Contornear el cuerpo mineral (contorno interno y
  externo) en el plano.

• Se dibujan los perfiles a una escala dada,
  incluyendo en los mismos los resultados del contorneo (Fig.
  2.7).

• Se calculan las áreas en los perfiles por su
  semejanza con figuras geométricas sencillas

• Se calculan los volúmenes entre perfiles
  utilizando las siguientes fórmulas:

Cuando la diferencia entre las áreas calculadas
no supera el 40 % se utiliza la fórmula del
trapezoide

Vi-ii = (S1+S2)/2 x L

Si y Sii –áreas de los perfiles
contiguos

L – distancia entre perfiles

Si la diferencia es mayor del 40 % se utiliza la
fórmula del cono truncado

Vi-ii = x
L

El cálculo del volumen en los flancos se realiza
por las fórmulas de la cuña o el cono en
dependencia de la forma aproximada del bloque en los
extremos.

V cuña =1/ 2 S*L

Vcono=1/3Sx L

• Estimación de los valores promedios de los
  parámetros para cada bloque (ley del componente
  útil)

Estimación de la ley media de cada perfil
limítrofe a partir de la media aritmética o media
ponderada por la potencia.

Ci = (C1*m1+C2*m2+ +Cnmn)/ (m1+ m2+ +mn) (perfil
I)

Cii= (C1*m1+C2*m2+ +Cnmn)/ (m1+ m2+ +mn) (perfil
II)

Posteriormente se calcula el valor medio del bloque
ponderando por el área de cada perfil.

Ci-ii = (Ci Si +CiiSii)/(Si+Sii)

Se calcula el valor promedio de la masa
volumétrica para cada bloque usando el mismo
procedimiento

• Cálculo de las reservas de menas y del
  componente útil en cada bloque

Qi-ii = Vi-ii*di-ii

Pi-ii = Qi-ii*Ci-ii

• Cálculo de las reservas totales del
  yacimiento por la sumatoria de las reservas de los bloques
  individuales

Qt = Qi-ii + Q ii-iii +
······ +
Qn-1,n

Pt = Pi-ii + P ii-iii +
··········
+ Pn-1,n

El método de las secciones en todas
sus variantes permite tener en cuenta de manera más
completa las particularidades de la constitución
geológica del yacimiento, la morfología y las
condiciones de yacencia de los cuerpos minerales (Lepin y
Ariosa,1986). El método posee desventajas importantes. En
primer lugar se basa en la interpolación rectilínea
de los datos de exploración entre las secciones contiguas
y por eso es inaplicable si la estructura
tectónica del objeto es compleja. Además si
distancias entre los perfiles son grandes se puede incurrir en
errores groseros en la determinación de los
volúmenes. Por este motivo, no se recomienda este
método durante los estadios iniciales del estudio
geológico del yacimiento, especialmente si se supone una
constitución geológica compleja.

En segundo lugar, al calcular las reservas
de mineral útil mediante este método no se utilizan
los datos de exploración obtenidos en los puntos dentro
del bloque, sino solo los ubicados en las secciones principales
de exploración.

Análisis
exploratorio de datos

3.1 Compositación o
regularización

Generalmente los intervalos de muestreo en los pozos de
exploración no coinciden con los intervalos de trabajo en
la fase de estimación de recursos. Los intervalos de
muestreo son siempre menores pues se busca revelar la
variabilidad espacial de las variables que se estudian. El
cálculo de los compósitos no es más que un
procedimiento mediante el cual las muestras de los
análisis se combinan en intervalos regulares (igual
longitud), que no coinciden con el tamaño inicial de las
muestras. La ley del nuevo intervalo se calcula usando la media
ponderada por la longitud de los testigos que contribuyen a cada
compósito y la masa volumétrica en caso de ser
variable. El objetivo de la regularización según
Barnes, 1980 es obtener muestras representativas de una unidad
litológica o de mineralización particular las
cuales pueden ser usadas, a través de una función
de extensión, para estimar la ley de un volumen mucho
mayor de la misma unidad.

Entre las principales razones y beneficios de la
regularización tenemos:

El análisis geoestadístico exige muestras
de igual longitud (similar soporte).

La compositación reduce la cantidad de datos y
por consiguiente el tiempo de cálculo o
procesamiento.

Se producen datos homogéneos y de más
fácil interpretación.

Se reduce las variaciones erráticas (alto efecto
pepita) producto de muestras con valores extremadamente
altos.

El proceso incorpora la dilución como la
provocada por la explotación de banco con altura
constante en la minería a cielo abierto.

Existen muchos tipos de yacimientos minerales cada uno
de los cuales requiere de un tratamiento específico de los
datos de las muestras de manera que se logren los mejores
intervalos de compositación para la evaluación
del los mismos (Barnes, 1980). Básicamente existen 3 tipos
principales de compósitos y se usan en dependencia de la
naturaleza de
la mineralización y el método de
explotación:

Compósito de Banco(bench composite): Las muestras
se regularizan a intervalos que coinciden con la altura de los
bancos o una
fracción de esta. Se emplea para modelar los recursos de
yacimientos grandes, diseminados de baja ley que se explotan con
minería a cielo abierto (Yacimientos de Cobre
porfídico).

Compósito de Pozo (down hole composite): Las
muestras se combinan a intervalos regulares comenzando desde la
boca del pozo.

Compósito Geológico (geological
composite): Las muestras se combinan a intervalos regulares pero
respetando los contactos geológicos entre las distintas
unidades. Este método se emplea para prevenir la
dilución del compósito en el contacto
estéril mineral y donde se logra mayor control sobre el
proceso de regularización.

El empleo de compósito de banco o de pozo en
estos casos provoca una distorsión de la
distribución de la ley ya que se puede adicionar mineral
de baja ley a la zona mineral o mineral de alta ley al
estéril.

Para escoger la longitud de regularización se
emplean las siguientes reglas empíricas:

• El tamaño del compósito se selecciona
  entre la longitud media de las muestras y el tamaño
  del banco

• Para el caso de los cuerpos en los que su
  análisis se hace de forma bidimensional, es necesario
  computar por pozos una media ponderada de los valores de
  todas las variables de interés que abarque todas las
  muestras positivas del intervalo mineralizado.

• No se debe regularizar muestras grandes en
  intervalos más pequeños pues se introduce una
  falsa idea de continuidad espacial (fig. 3.1).

Figura 3.1 Impacto provocado al regularizar muestras
grandes en intervalos pequeños.

3.2 Análisis exploratorio de
datos.

Antes de proceder con la estimación de reservas
propiamente dicha se debe, siempre que sea posible, realizar un
análisis estadístico de los datos disponibles o los
generados a partir del cálculo de los compósitos
con el objetivo de caracterizar el comportamiento
estadístico de las distintas variables en el
depósito y en las unidades geológicas (dominios)
que lo integran.

La organización de los datos cuantitativos y
su análisis pueden consumir el 50 % de tiempo necesario
para realizar la estimación de reservas. El
análisis exploratorio de datos está dirigido a
resolver las siguientes cuestiones:

• Identificar y eliminar los posibles
  errores

• Caracterización estadísticas de las variables de
  interés

• Documentar y entender las relaciones entre las
  variables

• Revelar y caracterizar la continuidad espacial de
  las variables (potencia y contenido del componente
  útil)

• Identificar y definir los dominios geológicos
  que requieren un tratamiento independiente durante la
  estimación de recursos.

• Identificar y caracterizar las muestras con valores
  extremos (outliers)

El cálculo de la estadística básica
y el estudio de la distribución de frecuencias de los
parámetros constituyen las principales herramientas
que posibilitan el análisis estadístico de los
datos. Los resultados de esta etapa complementan el modelo
geológico y se emplean en la modelación de
recursos.

La estadística básica se calcula para las
muestras originales y compositadas en cada dominio
geológico, los cuales incluyen distintos tipos
litológicos, tipos de alteración hidrotermal,
dominios estructurales y zonas o sectores en las que se reconoce
(o se sospecha) que la distribución estadística de
la variable es diferente.

3.2.1 Estadística descriptiva

El análisis estadístico comienza con el
estudio de la distribución de frecuencia la cual indica
como se distribuyen las muestras en intervalos regulares de los
posibles valores. A partir de aquí se construyen los
histogramas y gráficos de frecuencia cumulativa. El
estudio del histograma permite extraer conclusiones sobre el tipo
de distribución que siguen los datos, la presencia de
valores huracanados y la posible existencia de poblaciones
complejas (bimodalidad).

Al histograma calculado se le ajusta un modelo
teórico de distribución. En la práctica de
la estimación de recursos se emplean mayoritariamente el
modelo de distribución normal o gaussiana y el modelo
lognormal de 2 y tres parámetros.

Si el histograma del parámetro estudiado es
simétrico en forma de campana y la distribución de
frecuencia cumulativa se plotea como una línea recta en el
papel probabilístico normal entonces los datos se ajustan
al modelo de distribución gaussiano. Este tipo de modelo
se observa poco en los yacimientos minerales excepto en aquellos
de origen sedimentario.

La función de densidad de probabilidades que
describe matemáticamente esta distribución esta
dada por la siguiente ecuación

Donde

f(x)- función de densidad de
probabilidad

( – media

s- desviación estándar

El gráfico de la función de densidad de
probabilidad, conocida como curva normal, se muestra en la figura
3.2.

Figura 3.2 –Gráfico de la
distribución normal

Una propiedad muy
útil de la distribución normal es que el
área bajo la curva en un intervalo específico puede
ser fácilmente calculada. Por ejemplo, el 68 % de los
valores de la variable caen en el intervalo µ(s, el 95% en
el intervalo µ(2s y el 99% en el intervalo
µ(3s.

Si el histograma del parámetro estudiado es
asimétrico, formando una cola hacia la derecha y la
frecuencia cumulativa se grafica como una línea recta en
el papel probabilístico lognormal entonces los datos se
ajustan al modelo de distribución lognormal. Cuando los
datos poseen estás características la variable
original se transforma calculando el logaritmo natural de sus
valores. El histograma de la variable transformada se ajusta al
modelo gaussiano.

Este tipo de distribución se encuentra en muchos
problemas de evaluación de reservas, donde existe una gran
cantidad de valores bajos y unos pocos valores altos que definen
el yacimiento.

La función de densidad de probabilidades que
describe matemáticamente la distribución lognormal
esta dada por la siguiente ecuación.

Donde ( – media de los logaritmos de x

( – desviación estándar de los logaritmos
de x

Los gráficos de probabilidad o frecuencia
acumulada (normal o lognormal) son también de mucha
utilidad para
este análisis. En primer lugar permite corroborar el
modelo de distribución al que se ajusta la variable y
también calcular los principales parámetros
estadísticos que describen la distribución. En
muchos casos los gráficos obtenidos al representar la
frecuencia acumulada no constituyen líneas rectas sino
múltiples segmentos y curvas con sus respectivos puntos de
inflexión. Estos puntos de cambios de pendiente se emplean
para separar poblaciones complejas, siempre y cuando las
subpoblaciones posean coherencia espacial y una lógica
explicación geológica..

Una desviación típica de los
gráficos de probabilidad es una curva hacia abajo en el
extremo inferior. Esta curva representa un exceso de muestras con
leyes bajas comparado con lo que se debe esperar si la
distribución fuese lognormal. En los depósitos de
cobre porfídico, por ejemplo, esto se explica por
intrusiones tardías débilmente mineralizadas o
diques estériles posteriores a la mineralización.
Los datos deben ser examinados para determinar la fuente de las
muestras de bajo contenido y valorar si esta población ha sido o puede ser cartografiada
y estimada de forma independiente. Este mismo comportamiento del
gráfico de probabilidad puede originarse al representar
una distribución normal en un papel probabilístico
lognormal.

Otra desviación muy común de la
línea recta en el gráfico de probabilidades es una
curva de mayor pendiente en el extremo superior. Esto representa
un exceso de muestras con alto contenido lo cual puede ser
causado por la superposición de 2 poblaciones. Un ejemplo
de esto puede ser vetas de alta ley que cortan
mineralización diseminada de baja ley. Otras causas de
muestras con valores muy altos pueden ser los pequeños
sectores dentro del cuerpo altamente favorables para hospedar
mineralización producto de su alta permeabilidad,
propiedades químicas favorables, enriquecimiento
secundario o removilización metamórfica. Como la
mineralización de alta ley generalmente posee menor
continuidad que la de baja ley el origen de estas zonas debe ser
identificado y su estimación realizada de forma
independiente.

Una vez obtenidos los histogramas y gráficos de
probabilidades se calculan algunos parámetros de la
estadística
descriptiva que caracterizan numéricamente la
distribución estadística.

Los principales estadígrafos que
deben ser calculados para las distintas variables son:

Números de datos (muestras o
compósitos)

Medidas de tendencia central (media, moda,
mediana)

Medidas de dispersión (varianza,
desviación estándar, rango y coeficiente de
variación)

Medidas de forma (asimetría y
kurtosis)

3.2.1.1 Medidas de tendencia central

La media aritmética es el promedio de los
n valores medidos. Posee el inconveniente de que es muy
sensible a la presencia de valores extremos en los datos. La
media o esperanza matemática
se calcula por la fórmula siguiente

La moda es valor más probable o frecuente de la
variable estudiada

La
mediana es el punto central de los valores observados si se
organizan en orden ascendente. La mitad de los valores caen por
debajo de la mediana y la otra mitad por encima.

Cuando la variable se ajusta al modelo normal la moda,
la mediana y la media coinciden, si la distribución es
lognormal, la moda es mayor que la mediana y esta a su vez es
mayor que la media.

Cuando la distribución es asimétrica los
valores medios de la ley u otro parámetro estimados a
partir de una simple media aritmética están
sesgados y no se confirma posteriormente durante la producción. Si los datos se distribuyen
lognormalmente, la población se puede definir como una
población lognormal de dos parámetros (media y la
varianza de la población logarítmica), entonces el
valor medio de este tipo de distribución se obtiene por la
fórmula siguiente:

( = e[(+ var/2]

Donde:

( = Valor medio estimado de la variable

( = Media de la distribución de los logaritmos de
la variable

var = varianza de la distribución de los
logaritmos de variable.

Los valores ( y var pueden ser calculados por las
fórmulas anteriormente descritas o estimados a partir del
gráfico de probabilidad (fig. 3.5). La media de los
logaritmos coincide con el percentil 50 mientras que la
desviación estándar es SD =0.5(X16-X84).

Puede ocurrir que al representar los datos
logarítmicos en un diagrama de
probabilidad, estos no se ajusten exactamente a una recta,
mostrando una cierta curvatura en el comportamiento, lo que es
indicativo de la presencia de una población lognormal de
tres parámetros (Fig. 3.5). Este tercer parámetro,
denominado constante aditiva ((), se puede calcular
como:

( = [ x50 – ( x75 . x25 ) ] / (x25
+ x75 – 2.x50)

donde x25, x50 y x75 los valores de los percentiles 25,
50 y 75.

Este valor ( se añade a la población
original de datos. A continuación, se realiza la
transformación logarítmica obteniéndose una
nueva población ln(xi + (), la cual si se ajusta a una
distribución lognormal. El valor de ( estimado por este
método es tentativo y puede ser modificado de modo que se
logre el mejor ajuste posible.

Figura 3.5 Gráficos de probabilidad de una
distribución lognormal a)población lognormal de 2
parámetros b) población lognormal de 3
parámetros.

Para calcular, en este caso, la media del
parámetro se aplica el procedimiento descrito para la
población de dos parámetros, sustrayéndose
el valor de la constante aditiva al resultado final.

3.2.1.2 Medidas de dispersión

Varianza: La varianza de los datos,??????se
calcula de acuerdo a:

La varianza es la desviación cuadrática
promedio de los datos respecto a su valor central, esta medida es
sensitiva a valores extremos.

Desviación estándar: La
desviación estándar se calcula como la raíz
cuadrada de la varianza. Esta medida con frecuencia se prefiere
en lugar de la varianza debido a que sus unidades son las mismas
que la variable que se estudia.

Rango: Es la diferencia entre el máximo y
el mínimo.

3.2.1.3 Medidas de forma

Coeficiente de simetría: El descriptor
más utilizado para medir la forma de la
distribución es el coeficiente de asimetría. Debido
a la manera en que se calcula este coeficiente los valores del
mismo pueden estar afectados por la presencia de valores extremos
en los datos. Un sólo valor extremo puede influenciar
notablemente este coeficiente pues la diferencia entre cada valor
y la media es elevado al cubo. La distribución normal
estándar es perfectamente simétrica, Sk = 0. Esta
medida se calcula como:

Sk ( 0 Distribución asimétrica
negativa

Sk = 0 Distribución simétrica

Sk ( 0 Distribución asimétrica
positiva

Coeficiente de variación: Este coeficiente
se usa como una alternativa al coeficiente de asimetría.
Se emplea, principalmente, para distribuciones en las cuales
todos sus valores son positivos y cuya asimetría es
también positiva. Aunque puede ser utilizado para
distribuciones con asimetría negativa en ellas su
importancia como índice de forma decrece
considerablemente. Este coeficiente es una medida de
dispersión adimensional, y no está definido para el
caso en que la media es cero. Se calcula como la
desviación estándar dividida por la media de los
datos.

Un coeficiente de variación mayor que uno indica
la presencia de algunos valores erráticos en la muestra
los cuales pueden tener una gran influencia en la
estimación.

Según Finney (1941) una manera práctica de
saber si los datos se ajustan a una distribución normal o
lognormal es calcular el coeficiente de variación y
verificar si este es mayor o menor que 1.2; si es mayor que este
valor (gran dispersión de los valores) entonces la
distribución es lognormal, en caso contrario el modelo es
normal.

Noble, 2000 propone las siguientes reglas para
interpretar el coeficiente de variación.