Metrología avanzada – Standards and Calibrators (página 2)

Enviado por Ram�n Adrian Delgado Corral

Partes: 1, 2

Setup and stability of the part.

Quality and sharpness of tooling.

Quality and maintenance of machine tools.

Excessive clamping.

Size of the part.

The material the part is made from.

Heat treating.

Plating.

None of these problem are addressed with the use of solid
modeling programs.

The quote Dimensioning and Tolerancing ASME Y14.5M –
1994.

"Caution: if CAD/CAM database models are used and they
do not include tolerantes, these tolerante must be expressed
outside of the database to reflect design requirements."

The most effective way to communicate design intent is through
the probe use of geometric dimensioning and tolerancing.

2.2 ORIENTATION, PROFILE AND POSITION
CONTROLS

2.2.1 Orientation

Orientation is the general term used to describe the angular
relationship between features. Orientation controls include
parallelism, perpendicularity, angularity, and, in some cases,
profile. All orientation controls must have datums. It makes no
sense to specify a pin, for instance, to be perpendicular. The
pin must be perpendicular to some other feature. The other
feature is the datum.

Chapter Objectives

After completing this chapter, you will be able to

■ Specify tolerances that will control flat
surfaces parallel, perpendicular, and at some basic angle to
datum features

■ Specify tolerances that will control axes parallel,
perpendicular, and at some basic angle to datum features

The orientation of a plane surface controlled by two parallel
planes and an axis controlled by a cylindrical tolerance zone
will be discussed in this chapter. When a plane surface is
controlled with a tolerance zone of two parallel planes, the
entire surface must fall between the two planes. Since
parallelism, perpendicularity, angularity, and profile control
the orientation of a plane surface with a tolerance zone of two
parallel planes, they also control flatness if a flatness
tolerance is not specified. When it is desirable to control only
the orientation of individual line elements of a surface, a note,
such as EACH ELEMENT or EACH RADIAL ELEMENT, is placed beneath
the feature control frame.

When an axis is controlled by a cylindrical tolerance zone,
the entire axis must fall inside the tolerance zone. Although
axes and center planes of size features may be oriented using two
parallel planes, in most cases, they will be controlled by other
controls, such as a position control, and will not be discussed
in this chapter. The position control is a composite control,
which controls location

and orientation at the same time. Parallelism,
perpendicularity, and angularity are often used to refine the
orientation of other controls such as the position control.

Parallelism

Definition.- parallelism is the condition of a surface or
center plane, equidistant at all points from a datum plane; also,
parallelism is the condition of an axis, equidistant along its
length from one or more datum planes or a datum axis.

Specifying parallelism of a flat surface

In a view where the surface to be controlled appears as a
line, a feature control frame is attached to the surface with a
leader or extension line, as shown in Fig. 6-1. The feature
control frame contains a parallelism symbol, a numerical
tolerance, and at least one datum. The datum surface is
identified with a datum feature symbol. Parallelism tolerance of
a flat surface is a refinement of the size tolerance, Rule #1,
and must be less than the size tolerance. The size feature may
not exceed the maximum material condition (MMC) boundary, and the
thickness at each actual local size must fall within the limits
of size.

Interpretation.

The surface being controlled in Fig. 6-1 must lie
between two parallel planes separated by the parallelism
tolerance of .005 specified in the feature control frame. The
tolerance zone must also be parallel to the datum plane. In
addition, the surface must fall within the size tolerance, the
two parallel planes .020 apart. The entire part in Fig. 6-1 must
fit between two parallel planes 1.020 apart. The controlled
surface may not exceed the boundary of

Figure 6-1 Specifying a plane surface
parallel to a plane surface.

2.2.2 Profile

Profile is a surface control. It is a powerful and versatile
tolerancing tool. It may be used to control just the size and
shape of a feature or the size, shape, orientation, and location
of an irregular-shaped feature. The profile tolerance controls
the orientation and location of features with unusual shapes,
very much like the position tolerance controls the orientation
and location of holes or pins.

Chapter Objectives

After completing this chapter, you will be able to

■ Specify a profile tolerance

■ Explain applications of a profile tolerance zone

■ Properly apply datums for the profile tolerance

■ Explain the need for a radius control with a
profile

■ Explain the combination of a profile tolerance with
other geometric controls

■ Specify coplanarity

■ Properly apply composite profile tolerancing

Definition

A profile is the outline of an object. Specifically, the
profile of a line is the outline of an object in a plane as the
plane passes through the object. The profile of a surface is the
result of projecting the profile of an object on a plane or
taking cross sections through the object at various
intervals.

Specifying Profile

A profile view or section view of a part is dimensioned with
basic dimensions. A true profile may be dimensioned with basic
size dimensions, basic coordinate dimensions, basic radii, basic
angular dimensions, formulas, or undimensioned drawings. The
feature control frame is always directed to the profile surface
with a leader. Profile is a surface control; the association of a
profile tolerance with an extension or a dimension line is
inappropriate. The profile feature control frame contains the
profile of a line or of a surface symbol and a tolerance. Since
profile controls are surface controls, cylindrical tolerance
zones and material conditions do not apply in the tolerance
section of profile feature control

Figure 12-1 Specifying profile of a surface

2.2.3 Position, General

Position is a composite tolerance that controls both the
location and the orientation of size features at the same time.
It is the most frequently used of the 14 geometric
characteristics. The position tolerance significantly contributes
to part function, part interchangeability, optimization of
tolerance, and communication of design intent.

Chapter Objectives

After completing this chapter, you will be able to

■ Specify position tolerance for the location of
a size feature

■ Interpret tolerance specified at the regardless
of feature size (RFS) condition

■ Calculate bonus and shift tolerances for
features specified at the maximum material condition (MMC)

■ Specify position tolerance and calculate the
minimum wall thickness at the least material condition (LMC)

■ Calculate boundary conditions

■ Calculate tolerances specified with zero
positional tolerance at MMC

Definition

The tolerance of position may be viewed in either of the
following two ways:

■ A theoretical tolerance zone located at true
position of the toleranced feature within which the center point,
axis, or center plane of the feature may vary from true
position

■ A virtual condition boundary of the
toleranced feature, when specified at MMC or LMC and located at
true position, which may not be violated by its surface or
surfaces

Specifying the Position Tolerance

Since the position tolerance controls only size features, such
as pins, holes, tabs, and slots, the feature control frame is
always associated with a size dimension. In Fig. 7-1, the hole is
located and oriented with the position control. In this case, the
feature control frame is placed under the local note describing
the diameter and size tolerance of the hole. The location of true
position of this hole, the theoretically perfect location of the
axis, is specified with basic dimensions from the datums
indicated in the feature control frame. Once the feature control
frame is assigned, an imaginary tolerance zone is defined and
located about true position. The datum surfaces have datum
feature symbols identifying them. Datums A, B, and C identify the
datum reference frame in which the part is to be positioned for
processing.

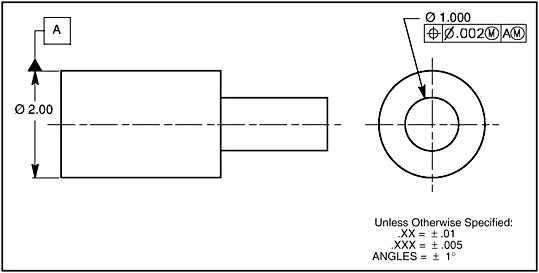
Interpretation The feature control frame is a sentence in the
GD&T language; it must be specified correctly in order to
communicate design intent. The feature control frame in Fig. 7-1
tells the location tolerancing story for the hole in this part:
it has a cylindrical tolerance zone .010 in diameter, the full
length of the feature, specified at RFS, is perfectly
perpendicular to datum plane A, located a basic 2.000 inches up
from datum B, and a basic 3.000 inches over from datum

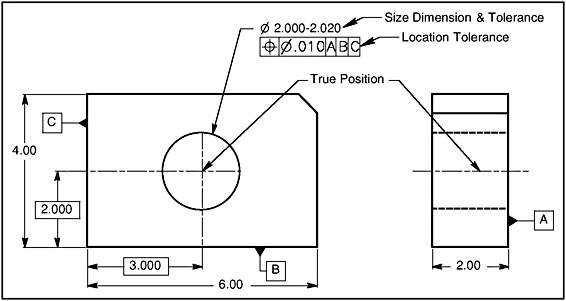
Figure 7-1 Location of a size feature with a
position tolerance at RFS

2.2.4 Position, Location

The most important function of the position control is to
locate features relative to datums and to one another. The
position control is one of the most versatile of the 14 geometric
controls. It controls both the location and the orientation of
size features and allows the application of maximum material
condition (circle M), least material condition (circle L) to
features being controlled and to datum features of size. Most of
the major applications of the position control are discussed in
this chapter. Even though coaxiality is the location of one
feature to another toleranced with the position control, it is a
separate topic and will be discussed in the next chapter.

Chapter Objectives

After completing this chapter, you will be able to

■ Calculate tolerances for floating and fixed
fasteners

■ Specify projected tolerance zones

■ Apply the concept of multiple patterns of
features

■ Demonstrate the proper application of composite
tolerancing

■ Demonstrate the proper application of two
single-segment feature control frames

■ Tolerance nonparallel holes

■ Tolerance counterbores

■ Tolerance noncircular features at MMC

■ Tolerance symmetrical features at MMC

Floating Fasteners

Because of the large number of fasteners used to hold parts
together, tolerancing threaded and clearance holes may be one of
the most frequent tolerancing activities that an engineer
performs. Often, due to ignorance, habit, or both, fasteners are
toleranced too tightly. This section on fasteners attempts to
provide the knowledge that allows engineers to make sound
tolerancing decisions for floating and fixed fasteners.

The floating fastener got its name from the fact that the
fastener is not restrained by any of the members being fastened.
In other words, all parts being fastened together have clearance
holes in which the fastener can float before being tightened. The
floating fastener formula is

Where T is the tolerance at MMC, H is the hole
diameter at MMC, and F is the fastener diameter at MMC,
the nominal size of the fastener. The tolerance derived from this
formula applies to each hole in each part.

The floating fastener formula is simple to remember. The hole
has to be larger than the fastener. The difference between the
sizes of the hole and the fastener is the location tolerance, as
shown graphically in Fig. 8-1.

Figure 8-1 Floating fastener

Once the fastener and the tolerance have been selected, it is
a simple matter to calculate the MMC hole diameter. All too
often, many designers simply use a reference chart for
tolerancing fasteners and have little understanding of how these
numbers are derived. If there is doubt about which tolerance to
use, specify zero at MMC. Zero positional tolerance will provide
all of the tolerance

2.2.5 Position, Coaxiality

One of the most common drawing errors is the failure to
specify coaxiality tolerance. Many practitioners think coaxiality
tolerance is unnecessary or are not even aware that coaxiality
must be toleranced. The position tolerance used to control
coaxiality will be discussed in this chapter.

Chapter Objectives

After completing this chapter, you will be able to

■ Explain the difference between position,
runout, and concentricity

■ Specify position tolerance for coaxiality.

■ Specify coaxiality on a material condition
basis

■ Specify composite positional control of coaxial
features

■ Tolerance a plug and socket

Definition

Coaxiality is that condition where the axes of two or more
surfaces of revolution are coincident.

Many engineers produce drawings similar to the one in Fig.
9-1, showing two or more cylinders on the same axis. This is an
incomplete drawing because there is no coaxiality tolerance. It
is a misconception that centerlines or the tolerance block
control the coaxiality between two cylinders. The centerlines
indicate that the cylinders are dimensioned to the same axis. In
Fig. 9-1, the distance between the axes of the Ø
1.000-inch and Ø 2.000-inch cylinders is zero. Of course,
zero dimensions are implied and never placed on drawings. Even
though the dimension is implied, the tolerance is not; there is
no tolerance

Figure 9-1 Definition"two surfaces of
revolution on the same axis.

indicating how far out of coaxiality the axes of an acceptable
part may be. Many practitioners erroneously think title block
tolerances control coaxiality. They do not. See Rule #1 in
Chapter 4, "the relationship between individual features," for a
more complete discussion of the tolerance between individual
features.

There are other methods of controlling coaxiality such as a
note or a dimension and tolerance between diameters, but a
geometric tolerance, such as the one in Fig. 9-2, is preferable.
The position control is the appropriate tolerance for coaxial
surfaces of revolution that are cylindrical and require the
maximum material condition (MMC) or the least material condition
(LMC). The position control provides the most tolerancing
flexibility.

Figure 9-2 Two surfaces of revolution
toleranced for coaxiality.

2.3 THE RULE OF 10%

The rule of 10% said that if tolerance is an element of t,
then the instrument used to demonstrate compliance with the
specification must have an uncertainty equal to or better than
t/10. In practice it is sometimes difficult to obtain even t / 5
but, whatever the tolerance and uncertainty, it is always
necessary to take a decision.
The relevant standard in this area is the UNE-EN ISO
14253-1:1999 – geometrical product specification (GPS). Inspection
by measurement Parts and measuring equipment. Part 1: decision to
test the
compliance or noncompliance with specifications. (ISO
14253-1:1998).

2.4 CALIBRATOR PASS – NOT PASS

This is one of the fastest methods for measuring external
threads and consists of a pair of rings threaded pass – not pass
(B and C as shown in Figure 3.2.23).

These sizes are fixed to the limits of tolerance of the part.
Its implementation is simply screw on the side. To enter without
passes must force over the length of the thread and not going to
be introduced no more than two threads before they are stuck.

These gauges indicate only if the inspected part is not within
tolerance (attributes). They did not specify what the actual size
of the screw, it becomes necessary to use any of the method
described above.
There are also caliber threaded pass – not pass for the
inspection of internal threads (A, D, E and G in figure 3.2.23).
They work under the same principle of pass – not pass, in this
case, the caliber of not enter a spin when it passes over, but
not another. This is perhaps the most practical method for
measuring internal threads, as though there are instruments that
provide data variables,
they are not available to smaller diameters