Aplicación de la proyección estereográfica en minería (página 2)

Enviado por Rosas Quispe, Edison Jes�s

Partes: 1, 2

PROYECCIÓN DE UN
PLANO

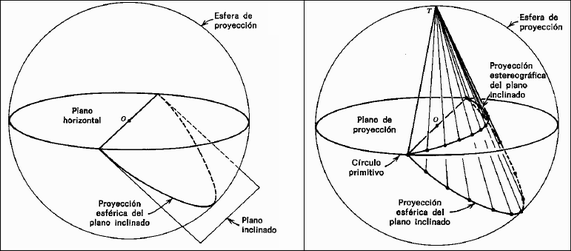
Se construye una esfera centrada en algún punto
"O" de la traza de afloramiento de un plano geológico
inclinado. El plano y su prolongación cortarán la
esfera según un círculo máximo o
círculo mayor.

Representación de un plano inclinado
(según Phillips 1971):

Representación de un plano inclinado con su
polo:

Esta proyección esférica hay que
representar en 2D. Como los mapas
mundi.

Para esto se proyectan todos los puntos de
la parte inferior (hemisferio Sur) del círculo
máximo al plano horizontal (ecuatorial o círculo
primitivo) mediante su unión con el punto cenital P. El
resultado es una ciclográfica.

Proyección estereográfica de un plano
inclinado (Phillips 1971):

Ejemplo gráfico de la proyección
estereográfica:

Cuantificación del ángulo de
inclinación de un plano:

Tipos de representaciones
estereográficas:

Existen diversas formas de
representación de los elementos planos y lineales en la
proyección estereográfica. Todos ellos se llevan a
cabo mediante el empleo de la
falsilla de Wulff que se obtiene a partir de la proyección
de los meridianos y paralelos de la esfera.

Diagrama de círculos máximos o
diagrama
beta:

Únicamente se utiliza para la
representación de elementos planos. Se obtiene por
proyección sobre el plano ecuatorial, del círculo
máximo de la superficie plana considerada. Este
círculo máximo representa la intersección
del plano con la esfera. En la figura 5.a. se muestra el
diagrama de círculos máximos correspondiente al
estudio de un macizo rocoso.

Figura

(Ver de izquierda a derecha)

Diagrama de círculos máximos
(beta).
Diagrama de polos (pi).

Diagrama de polos o diagrama pi

Cuando las medidas a representar en el diagrama son muy
numerosas, la representación mediante círculos
máximos puede dificultar la lectura de
los resultados en la falsilla, por lo que se suele recurrir a los
diagramas de
polos o diagramas pi.

En este tipo de diagramas se representan
únicamente los polos de los planos o rectas, es decir la
intersección de la recta con la esfera en el caso de
elementos lineales o la intersección de la normal al plano
con la esfera si se trata de elementos planos.

En la figura b. se muestra la representación pi
de los datos
correspondientes al mismo macizo rocoso de la figura a. La
concentración de polos superior izquierda (S0) corresponde
con la estratificación de orientación aproximada
N30E 35 SE. Las otras dos concentraciones observadas (J1 y J2) de
orientaciones N60E 49NW y N160E 20SW corresponden a sendos
juegos de
diaclasas.

Diagrama de densidad de
polos

La proyección estereográfica de un
determinado elemento de la naturaleza,
nunca es tan exacta como la de líneas y planos
teóricos, ya que presentan irregularidades puntuales,
falta de ajuste con la geometría ideal, en muchos casos, y
posibles errores de precisión. Esto hace que se produzcan
dispersiones que, dependiendo de su magnitud, pueden o no
facilitar la interpretación de un polo o un
círculo máximo. De ser así y producirse una
gran dispersión de datos, será preciso recurrir a
un análisis estadístico de una muestra
grande de datos con el fin de determinar la dirección y buzamiento predominantes
(figura).

Este análisis estadístico no se puede
realizar mediante la proyección estereográfica ya
que se producirá una gran concentración de puntos
en la parte central del diagrama (figura b). Para realizar este
análisis se recurre a la proyección equireal,
empleando la falsilla de Schmidt, que nos permite el recuento
directo de los polos, calcular su valor
estadístico por unidad de superficie y determinar las
direcciones y buzamiento predominantes (figura a).

Figura: Diagrama de densidad de polos: (ver de izquierda
a derecha)

En proyección equiareal.
En proyección estereográfica
(equiangular).

Falsillas estereográficas

Son como un transportador de ángulos
en 2D que sirven para representar las orientaciones de los planos
y líneas de las respectivas proyecciones
ciclográficas.

Hay diferentes tipos de falsillas:

Falsillas equiareal (Schmidt):
geología estructural. Conserva las áreas
pero no los ángulos.
Falsillas equiangular (Wulf):
cristalografía. Conserva los ángulos
pero no las áreas.

Proyección de un plano con su
polo

Ejemplo: 120 / 40

Proyección de una línea

Ejemplo: 138 – 30

DEBILITAMIENTO
ESTRUCTURALMENTE CONTROLADO

Para que un bloque de roca pueda caerse del techo o de
una excavación, se necesita que quede separado del macizo
circundante cuando menos en tres discontinuidades estructurales
que se intersecten.

El debilitamiento estructuralmente controlado se puede
analizar mediante la técnica de la proyección
estereográfica que se describió anteriormente, Un
ejemplo sencillo de la aplicación de este método se
ilustra en el dibujo del
margen inferior que muestra una cuña de roca que cae del
techo de una excavación en roca fisurada. Una línea
vertical que atraviesa el vértice de la cuña tiene
que caer dentro de la base de la misma para que el debilitamiento
pueda producirse sin fricción cuando menos sobre uno de
los planos de fisuras.

Condiciones necesarias para que se
pueda producir una caída del techo.

En la representación estereográfica, la
línea vertical que pasa por el vértice de la
cuña se representa por el punto central de la red y las condiciones que se
estipulan en el párrafo
anterior quedarán cubiertas si los grandes círculos
que representan los planos de las juntas forman un dibujo cerrado
que rodee el centro de la red.

Esta verificación cinemática sencilla es muy útil para
prever las caídas potenciales del techo durante los
estudios preliminares de los informes de la
geología
estructural que se recabaron para proyectar la excavación
subterránea. Este método estereográfico
también se puede emplear para una apreciación mucho
más detallada de la forma y del volumen de
cuñas potencialmente inestables. Como lo muestra la figura
01.

En esta figura 01 se representan tres planos por sus
grandes círculos, marcados A, B y C.
Las líneas de los rumbos de estos planos están
marcados con a, b y c, y los trazos de los
planos verticales por el centro de la red y las intersecciones de
los grandes círculos están marcados ab,
ac y bc. Supongamos que un túnel cuadrado
con un claro s vaya en una dirección de 290º a
110° como se muestra en la parte inferior de la figura 01.
Las direcciones del rumbo de las líneas corresponden a las
trazas de los planos A, B y C sobre el techo
horizontal del túnel. Esas líneas del rumbo se
pueden combinar para que la figura triangular de tamaño
máximo se acomode en el techo del túnel, como lo
muestra la figura 01.

Figura 01. Construcción complementaria en
combinación con una proyección
estereográfica para determinar la forma y el volumen de
una cuña que se presenta estructuralmente en el techo de
un túnel.

En la vista de planta, el vértice de la
cuña se determina al localizarse el punto de
intersección de las líneas ab, ac y
bc proyectadas desde las esquinas de la base de la
cuña triangular como se muestra. La altura h del
vértice de la cuña sobre el techo horizontal del
túnel se localiza al hacerse una sección que pase
por el vértice y normal con respecto al eje del
túnel. Esta sección, marcado XX en la figura 01,
intersecta las trazas a y c en los puntos indicados
y estos puntos delimitan la base del triángulo como se
señala en el perfil XX. Los echados aparentes de los
planos C y A están indicados por los
ángulos α y
β, los que se miden sobre la
proyección estereográfica a lo largo de la
línea XX pasando por el centro de la red.

El volumen de la cuña se obtiene por
1/3·h X el área de la base de la
cuña, lo cual se determina en la planta de la figura
01.

Si tres fisuras se intersectan para formar una
cuña en el techo de una excavación
subterránea pero la línea vertical que pasa por el
vértice de la misma no cae dentro de la base de la
cuña, el debilitamiento sólo puede ocurrir con
fricción sobre uno de los planos de fisura o sobre una de
las líneas de intersección. Esta condición
se representa estereográficamente si la figura de
intersecciones formada por los tres grandes circulas cae a un
lado del centro de la red como se ilustra en el dibujo del margen
inferior.

Condiciones necesarias para un
debilitamiento con fricción de las cuñas del
techo

Una condición adicional que tendrá que ser
tomada en cuenta para que la cuña se pueda deslizar, es
que el plano o línea de intersección sobre la cual
se deslice tenga una inclinación mayor que al del
ángulo de fricción
Φ. Esta condición se
cumplirá si cuando menos una parte de la figura de
intersección cae dentro de un circulo que se logra al
descontar de la circunferencia exterior de la red la cantidad de
divisiones de grado que corresponden al ángulo de
fricción.

Condiciones estables de la
cuña

La construcción de la verdadera vista en planta
de la cuña obedece a los mismos principios que se
siguieron en la figura 01 y la construcción para el caso
que nos ocupa se ilustra en la figura 02. En este ejemplo, el
largo del rumbo de la traza c del plano C, se
define por la dimensión L.

Al determinarse la altura h de la cuña, el
perfil XX tiene que tomarse en ángulos rectos con respecto
a la línea ab que pasa por el centro de la red y la
intersección de los grandes círculos que
representan los planos A y B. El
ángulo α es el
echado verdadero de la línea de intersección de
esos dos planos.

Cuando la figura de intersección cae
completamente fuera del círculo de fricción, como
se muestra en el dibujo del margen, el peso gravitacional de la
cuña no es suficiente para vencer la resistencia de la
fricción del plano o de los planos sobre los cuales
debería deslizarse. En esas condiciones la cuña se
resistirá a deslizar.

Figura 02. Construcción de una verdadera
vista en planta y determinación de la altura de una
cuña donde se produce un debilitamiento como resultado de
un deslizamiento a lo largo de la línea de
intersección de los planos A y B.

En las paredes de una excavación en roca
fisurada, el debilitamiento de las cuñas puede presentarse
en una forma muy parecida a la del techo, excepto que las
caídas libres no son posibles y que todos los
debilitamientos en las paredes implican deslizamientos sobre un
plano o sobre la línea de intersección de dos
planos. A continuación presentamos dos métodos
para analizar el debilitamiento en las paredes.

El análisis del debilitamiento en las paredes:
método 1

Consideremos un túnel cuadrado que va en una
dirección de 250° a 70° a través de un
macizo en que se presentan tres series de fisuras. Estas fisuras
se representan, en la proyección estereográfica que
se muestra en el dibujo por los grandes círculos marcados
A, B y C.

Los trazos de los grandes círculos en este dibujo
se obtuvieron por la proyección sobre un plano
horizontal pasando por el centro de la esfera de
referencia. Para saber cuál es la forma de la cuña
en la pared del túnel, será necesario determinar la
forma de la figura de intersección proyectada sobre un
plano vertical.

Esta figura de intersección se obtiene por la
rotación de las intersecciones ab, bc
y ac de los grandes círculos en 90° alrededor
del eje del túnel. Se logra estereográficamente
esta rotación de la manera siguiente:

Se trazan los puntos ab, bc y ac
sobre una hoja limpia de papel de dibujo. Sobre el croquis se
indican el centro, el norte y el eje del
túnel.
Se coloca el croquis sobre la red meridiana por medio
de una aguja central de manera que el eje del
túnel coincida con el eje norte-sur de la
red.
Se gira cada una de las tres intersecciones sobre un
plano vertical al descontar 90º sobre los
círculos pequeños pasando por los puntos
ab, bc y ac.

Hay que señalar que la rotación de todos
los puntos tiene que hacerse en la misma dirección y
también que el circulo pequeño que pasa por
ac se sale de la circunferencia de la red en x y
vuelve a entrar en un punto diametralmente opuesto, x'.
Este procedimiento
permite a todos los puntos de intersección encontrarse en
el mismo hemisferio y que la proyección sobre el plano
vertical tenga sentido.

Márquense las intersecciones giradas
ab’, bc’ y ac’ y
encuéntrense los grandes círculos que pasan por
pares de puntos de intersección. Las líneas del
rumbo de esos grandes círculos representan las trazas de
los planos de fisuras sobre las paredes verticales del
túnel.

Se muestra la construcción completa en la parte
superior de la figura 03, lo que da la proyección
estereográfica de los planos y sus intersecciones de un
plano vertical paralelo a las paredes del
túnel.

La construcción de la vista verdadera de la
cuña en la pared sigue el mismo procedimiento que el que
se usó para el techo (figuras 01 y 02). Las trazas
a’, b’ y c’ de las fisuras
en la pared son paralelas a las líneas de los rumbos de
los grandes círculos en la proyección
estereográfica vertical. Las líneas de
intersección ab’, bc’ y
ac’ que se ven en la pared vertical son
también paralelas a las líneas que parten del
centro de la proyección vertical a los puntos
ab’ bc’ y ac’.

Es importante señalar que las vistas en las
partes inferiores de las figuras 03 y 04 representan las trazas
de las fisuras que se ven en la pared norte vista desde el
interior del túnel o en la pared sur vista desde el
exterior del túnel, mirando hacia 340º. Esto
es comprobable si se comparan los rumbos
α,
β y
ξ de las trazas de los planos
A, B y C en la pared vertical, que se logran
con las proyecciones estereográficas, con las trazas
correspondientes en las vistas de la pared del túnel. Una
imagen de espejo de la vista dada en las partes inferiores
de las figuras 03 y 04 representa las trazas de las fisuras en la
pared sur vistas desde el interior o en la pared
norte vistas desde el exterior del túnel,
mirando hacia la dirección de 160º.

Es muy importante que se comprendan bien esas vistas, ya
que un error podría dar como resultado una
apreciación incorrecta de estabilidad así como la
aplicación de medidas correctivas indebidas.

Vista de los trazas de las fisuras en la pared
norte, mirándolo desde el interior del túnel a en
la pared sur mirándola desde el exterior del túnel
en una dirección de 340º.

Figura 03. Construcción de la vista
verdadera de una cuña en la pared de un túnel
mediante el Método 1.

La altura h de la cuña que se muestra en
la figura 03 se determina con un seccionamiento XX que pasa por
la punta de la cuña, y localizando los echados aparentes
k y θ de los
planos A’ y B’ que se ven en la
proyección vertical. Esta construcción es
idéntica a la que se empleó en la figura 01para
determinar la altura de la cuña en el techo del
túnel.

El análisis del debilitamiento de las paredes:
método 2

En este método, las trazas a, b y
c de las fisuras en la pared del túnel se localizan
con los echados aparentes
α β
y ξ de los planos
A, B y C en un plano vertical paralelo al
eje del túnel. En la figura 04 se ilustra cómo se
localizan estos echados aparentes.

Los trazos ab, bc y ac en la pared
se establecen al encontrarse los echados
Ψabt,
Ψbct
y
Ψact de las
proyecciones de estas líneas de intersección sobre
la pared vertical. El ángulo
Ψabt lo
da:

Donde
θab es el
ángulo entre el eje del túnel y laproyecci6n de la
línea de intersección ab sobre el plano
horizontal y
Ψab es el
echado verdadero de la línea de intersección
ab.

Los ángulos
Ψbct y
Ψabt se
localizan de la misma manera.

La altura h de la cuña se determina al
valorizar los ángulos
Ψbct
y
Ψact que
representan los echados de las líneas de
intersección que se ven en un plano vertical en
ángulos rectos con el eje del túnel. El
ángulo
Ψbct se
obtiene por: