Tarjetas de estudio de Teoría Cinético Molecular y Termodinámica (página 2)

A manera de ilustración presentamos el mapa Conceptual
para representar el concepto de Mapa
Conceptual dado al inicio de esta cuartilla.

Mapa conceptual del concepto dado de
mapa conceptual

Tarjetas de estudio de Teoría
Cinético Molecular y Termodinámica

Temas: Teoría Cinético
Molecular y Termodinámica

Autor:

Profesor Auxiliar

Departamento de Física

Universidad de
Matanzas "Camilo Cienfuegos"

Matanzas, Cuba.

Tarjeta de
estudio No. 1. Tema: Teoría Cinético
Molecular.

Tema: Teoría Cinético
Molecular (TCM). Líquidos y gases.

Temática: Fundamentos
de la TCM. Compresibilidad de los gases. Elasticidad de
los sólidos. Movimiento
Browniano. Calor y
temperatura.
Estructura de
los líquidos. Difusión. Viscosidad.
Ley de Stokes.
Presión
interna en los líquidos. Tensión superficial y
energía libre de la superficie de un líquido.
Fórmula de Laplace.
Fenómenos capilares: Fórmula de Jurín.
Descripción mecánica, estadística y termodinámica de un sistema de
partículas. Coordenadas termodinámicas. Postulados
de la teoría cinético – molecular. Modelo del
gas ideal.
Ecuación fundamental de la teoría cinético
molecular del gas ideal. Correcciones a la TCM. Energía
cinética media de traslación de una
molécula. Constante de Boltzmann. Teorema de Boltzmann
sobre la equipartición de la energía.
Energía interna. Calor específico molar de un
gas.

Objetivos.

1. Interpretar físicamente las leyes que
   abordan el tema y aplicarlas en el análisis de diferentes fenómenos,
   así como en la solución de problemas
   numéricos.
2. Interpretar diferentes fenómenos vinculados a
   la especialidad a partir de los postulados de la
   TCM.
3. Aplicar la ecuación fundamental de la
   teoría cinética del gas ideal y la
   ecuación de estado en la
   solución de problemas.
4. Describir los puntos de vistas macroscópicos y
   microscópicos para el análisis de los
   fenómenos en sistemas con
   muchas partículas.
5. Interpretar la temperatura del gas ideal en función
   de la energía cinética promedio de las
   moléculas respecto al centro de masa

Información teórica
básica.

• En este tema considerará un enfoque de
  promedios llamado teoría cinética molecular (TCM)
  en el que seguimos el movimiento de las partículas
  representativas de un gas y luego promediamos este comportamiento para todas las
  partículas.
• Los postulados de la TCM plantean que todas las
  sustancias están compuestas por moléculas las
  cuales se encuentran animadas de un movimiento continuo y
  desordenado llamado movimiento térmico o Browniano,
  entre las moléculas existen espacios intermoleculares y
  fuerzas de atracción y repulsión que son de
  naturaleza
  eléctrica y su influencia es de varios diámetros
  moleculares.
• Podemos afirmar que la temperatura es una medida
  cuantitativa del estado térmico de los cuerpos, por
  estar íntimamente vinculada a la energía interna
  y por tanto con la intensidad de su movimiento
  molecular.
• La cantidad de calor trasmitida de un cuerpo a otro
  depende de la naturaleza de la sustancia, de la masa del cuerpo
  y de la variación de su temperatura, por lo que Q = m c
  D t, donde C es el calor
  específico (cantidad de calor necesaria para variar la
  temperatura de un kilogramo masa de sustancia en un grado
  Celsius).
• Existen diferentes escalas termométricas pero
  trabajaremos fundamentalmente con la Fahrenheit, la Kelvin y la
  Celsius, siendo las expresiones que las relacionan:

y C
= k – 273

• La difusión es el proceso de
  penetración de las moléculas de una sustancia en
  los espacios intermoleculares de otra y se explica por la ley
  de Fick, la que plantea que: D m = –
  D D r
  /D x D
  SD t, donde D m es la masa del fluido difundido o
  transportada en el intervalo de tiempo
  D t, D s
  es el área de contacto entre las superficies de fluido,
  la cual es perpendicular a la dirección en que se transporta el fluido,
  D r
  /D x es el gradiente de densidad
  (densidad de masa por unidad de longitud) donde r = siendo evidente que a densidad es menor en la zona
  más avanzada de la difusión, pues la
  concentración de moléculas es menor en la medida
  en que estas avanzan, D es el coeficiente de difusión es
  decir la masa de fluido transportado a través de una
  superficie de 1m2 en un segundo, siendo El signo negativo
  indica que el transporte
  de masa se produce en el sentido en que disminuye la
  densidad.
• La viscosidad es el rozamiento interno entre capas de
  fluido y es debido a la cohesión entre moléculas,
  la ley de Newton
  plantea que f= -h D V/D t D S, siendo
  h el coeficiente de viscosidad del
  fluido, D V/D x el gradiente de velocidad y
  D S el área de contacto entre
  capas de fluido, significando el signo menos que la fuerza
  viscosa es de sentido contrario al movimiento.
• El volumen de
  líquido que fluye por un tubo es proporcional a la
  cuarta potencia del
  radio del tubo,
  al tiempo y al gradiente de presión e inversamente
  proporcional al coeficiente de viscosidad, por lo que V=
  -p r4/8h D P/D x D t,
  significando el signo menos que el incremento de volumen es
  menor en la medida en que aumenta el gradiente de
  presión.
• La ley de Poiseuille plantea que la velocidad media
  del flujo laminar (V) de un líquido por un tubo es
  proporcional al gradiente de presión del líquido
  y al cuadrado del radio del tubo e inversamente proporcional al
  coeficiente de viscosidad del líquido, por lo que
  V=-D P/D
  x r2/8h , significando el
  signo negativo que la velocidad de la corriente es de sentido
  contrario al gradiente de presión.
• Debido a la viscosidad un cuerpo que se mueve en el
  seno de un fluido arrastra consigo las capas de fluido con las
  que está en contacto, por lo que experimenta cierta
  resistencia en
  su movimiento, por parte del fluido. La fuerza de resistencia
  dependerá de la de la velocidad con que se mueva el
  cuerpo, de sus dimensiones y forma.
• La ley de Stokes para cuerpos de forma
  esférica, que se mueven con velocidades no muy grandes
  plantea que la fuerza de resistencia del fluido será
  directamente proporcional a la velocidad del cuerpo
  esférico, a su radio y al coeficiente de viscosidad del
  fluido, por lo que su expresión es f = 6p h rv.
• Tensión superficial se denomina al estado de
  tensión a que está sometida la capa superficial
  de un líquido, la que tiene su origen por la
  cohesión de las moléculas de la capa, siendo la
  fuerza de tensión superficial proporcional a la longitud
  de la capa superficial (al número de moléculas)
  por lo que F = a l, siendo
  a el coeficiente de tensión
  superficial a [ N/m] .
• El coeficiente de tensión superficial
  (a ) se puede disminuir con el
  aumento de la temperatura, ya que al aumentar esta, aumenta la
  distancia media entre las moléculas y con la
  adición de las sustancias detergentes, pues estas
  provocan que se reduzca el valor de la
  fuerza de tensión superficial.
• La energía libre de la superficie de un
  líquido es proporcional al área de la superficie,
  por lo que
• E = a S.
• La expresión de Laplace nos plantea que
  D P =± 2a (1/R1+1/R2) es decir
  que la presión adicional dependerá del valor del
  coeficiente de tensión superficial y del grado de
  curvatura de la capa superficial. Tomará valor positivo
  (+) si la superficie es convexa y negativa (-) si es
  cóncava. Si la superficie tiene una curvatura
  esférica R1= R2, por lo que
  D P =± 2a /R y si es plana D
  P = 0, ya que R1= R2 = a y 1/a =
  0.
• Si la fuerzas de cohesión entre las
  moléculas del líquido es mayor que la que existe
  entre las moléculas del líquido con las del
  sólido en que está contenido, el líquido
  tiende a disminuir el área de contacto con el
  sólido, separándose de el lo más posible,
  siendo el ángulo interfacial q >, planteándose que el líquido no moja
  al sólido, por lo que se denomina líquido no
  humectante, en caso contrario si q
  < el
  líquido moja al sólido y se denomina
  líquido humectante. Si q =
  00 el líquido se extiende por toda la
  superficie y se plantea que hay un mojado total y si
  q =p se
  plantea un no mojado total.
• El concepto de mojar o no es relativo pues hay
  líquidos que mojan a un sólido y no mojan a
  otros, por ejemplo el agua moja
  al vidrio y no
  moja a la parafina y el mercurio no moja al vidrio y sí
  moja al cobre.

• Para tubos capilares (de muy pequeño
  diámetro) la curvatura superficial o menisco es
  esférico, planteándose por Borelli y Jurín
  que h =, es
  decir que la altura a que se eleva la columna líquida
  por el tubo capilar es proporcional en razón inversa con
  el radio del tubo (r), siendo el término denominado constante
  capilar y q el ángulo
  interfacial. Si denominamos por R al radio de curvatura del
  menisco, tendremos que cos q =
  

, por lo que h =2a
/r gR.

• La ley de Avogadro nos plantea que el volumen ocupado
  por un gas a determinadas presiones y temperaturas es
  independiente del tipo de gas o del tamaño o masa de sus
  moléculas, este depende únicamente del
  número de moléculas (V a N). La ley de Boyle nos dice que la
  presión es inversamente proporcional al volumen (P
  a ) y la ley de Charles o de Gay-Lussac nos dice
  que el volumen es directamente proporcional a la temperatura (V
  a T). Todas estas leyes son
  válidas para gases cuyo comportamiento es ideal y nos
  llevan al planteamiento de la expresión k = , siendo k = 1,38066.
  10-23 J/K (Constante de Boltzmann). Si queremos
  expresarla en función del número de moles (n)
  hallamos la relación entre el número de
  moléculas (N) y la constante de Avogadro (NA
  = 6,023. 1023 moléculas/mol), lo que nos
  queda como:
  =k NA = R, siendo R la constante universal de los
  gases ideales. (R = 8,31 J/molK). Esta última
  expresión se puede formular como PV = nRT y se denomina
  ecuación de estado para los gases cuyo comportamiento es
  ideal.
• Los postulados de la TCM del gas cuyo comportamiento
  es ideal plantean que todas las sustancias están
  compuestas por moléculas las cuales se encuentran
  animadas de un movimiento continuo y desordenado llamado
  movimiento térmico o Browniano, que entre las
  moléculas existen espacios intermoleculares, que el
  volumen de las moléculas es una fracción
  despreciablemente pequeña comparada con el volumen
  ocupado por el gas y que entre las moléculas no existen
  fuerzas de interacción excepto durante los
  "choques", los que se plantean como perfectamente
  elásticos.
• La raíz cuadrada de V2 se llama
  velocidad media cuadrática (rms, root-mean-square) y es
  una clase de
  velocidad molecular promedio. Vrms= V2 =
  siendo P la
  presión y ρ la densidad. Dicha magnitud
  también se relaciona con la temperatura a través
  de la expresión: Vrms= 3kT/m
• Podemos afirmar que la temperatura es una medida
  cuantitativa del estado térmico de los cuerpos, por
  estar íntimamente vinculada a la energía interna
  y por tanto con la intensidad de su movimiento molecular,
  siendo K =
  kT.
• La cantidad de calor trasmitida de un cuerpo a otro
  depende de la naturaleza de la sustancia, de la masa del cuerpo
  expresada en moles y de la variación de su temperatura,
  por lo que Q = n C D T, donde C es
  el calor específico molar (cantidad de calor necesaria
  para variar la temperatura de un mol de sustancia en un
  Kelvin).

Ejercicios Resueltos:

1.- Sobre la superficie del agua se
deposita una aguja de acero grasienta
(que el agua no moja en lo absoluto) ¿ Qué
diámetro máximo podrá tener esta aguja para
mantenerse a flote?

Para que la aguja pueda mantenerse flotando sobre la
superficie del agua es necesario que la presión que ejerce
su peso sobre el área de apoyo no sea mayor que la
presión producida por la curvatura de la superficie del
líquido (D P) en el hueco que
se forma debajo de la aguja, la cual estará dirigida hacia
arriba.

Como la superficie de apoyo de la aguja en el
líquido es cilíndrica planteamos
R1=a y R2 = r,
siendo r el radio de la aguja, por lo que D P = a /r Þ D P
=2a /d.

Como es necesario que D P
³ P para que la aguja flote,
debemos plantear que:

2.-

En un recipiente que contiene Hg se introduce un tubo
capilar abierto cuyo diámetro (d) es de 3mm. La diferencia
entre los niveles de Hg entre el recipiente y en el tubo capilar
es de 3,7mm. ¿Qué radio de curvatura tendrá
el menisco del Hg que hay en el tubo capilar ?

Según la expresión de Laplace D P= ± 2a /R y como
q >
el
líquido es no humectante siendo el menisco convexo por lo
que , pero
según Borelli – Jurín r = por lo que cos r ghr//2a y
sustituyendo por los valores
cos l3,6.
103kg/m3 9,8 m/s23,7.
10-3m 1,5. 10-3m/2 0,5 N/m, por lo que cos
0,74 pero como
> q > , entonces el coseno es negativo, por lo que cos y como r = -R
cos ó R
= 2mm.

Evidentemente como el líquido es no humectante la
superficie de la columna líquida en el capilar
estará por debajo de la superficie del Hg contenida en la
vasija.

3.- Un recipiente que tiene una capacidad de 50 l
contiene oxígeno
a la presión manométrica de 6 atm a una temperatura de
47C.
Posteriormente se observa que a causa de una fuga la
presión manométrica descendió a 5 atm y la
temperatura bajó a 27C. Calcula:

1. La masa de oxígeno que había
   inicialmente en el recipiente.
2. La masa de oxígeno que se
   escapó.

Como el valor de presión que tenemos es
manométrico debemos expresarlo en presión absoluta,
donde: PABS== PMAN +1 atm y PABS = 6
atm.

También debemos expresar la temperatura en la
escala absoluta,
es decir en Kelvin, donde K = C+273 Þ T0= 320K y T = 300K

El valor de la constante universal de los gases cuyo
comportamiento es ideal será

R = 0,082 atm-l/mol K, atendiendo a las unidades en que
se expresan la presión y el volumen. Para poder calcular
la masa de oxígeno que había inicialmente debemos
hallar el número de moles, por lo que:
N=P0V0/RT0 donde

Conocemos que m = m N, donde
m es la masa molar y m la masa de
oxígeno expresada en kilogramo (kg). También
conocemos que la masa atómica del oxígeno es de 16g
y que una molécula de oxígeno tiene dos
átomos por tanto m = 32 g / mol
Þ m =
0,032 Kg/mol, por lo que m = 0,032 kg/ mol . 13,34 mol m= 0,043
kg.

Para calcular la masa de oxígeno que
escapó (D m) debemos primero
hallar el número de moles (n) de Oxígeno que
quedó en el recipiente, por lo que: n =PV/RT donde n= 12,2
mol.

m=m n donde m= 0,39 kg y para
calcular la masa de oxígeno que escapó planteamos
que:

D m=0,04 kg.

4.- La energía cinética media de una
molécula de N2 es de 3,1 10-21 J. a)
¿Qué presión ejercerán 2 moles que en
estas condiciones ocupan un volumen de 2,4 10-3
m3?

b) ¿ Cuál será la energía
cinética media de una molécula de H2 a
la misma temperatura?

a) Para calcular la presión utilizamos la
ecuación de estado para los gases cuyo comportamiento es
ideal, es decir PV = nRT, donde P=nRT/V, pero antes debemos
hallar la temperatura, por lo que debemos utilizar la
expresión EC=3/2KT, donde T= 2Ec/3K,
es decir T=2. 3,1. 10-21 J/3. 1,38. 10-23
J/K , donde T= 150 K.

b) Conocemos que la EC=3/2 KT por lo que la
energía cinética sólo depende de la
temperatura, por lo que la energía cinética de una
molécula de H2 a la misma temperatura que una
molécula de N2 será la misma, es decir
3,1. 10-21 J.

Ejercicios propuestos

1.- En un recipiente con agua se introduce un tubo
capilar abierto cuyo diámetro interior es de 1mm. La
diferencia entre los niveles de agua en el recipiente y del
líquido en el tubo capilar es de 2,8 mm. A) ¿
Cuál será el valor del radio de curvatura del
menisco en el tubo? B) ¿ Cuál será la
diferencia entre los niveles de agua en el recipiente y el tubo
capilar si este líquido moja perfectamente.

Represente gráficamente y explique si la
superficie del líquido en el tubo capilar está a un
nivel mayor o menor que la del líquido en el
recipiente.

2.- En un suelo
monolítico a costa de su porosidad (capilaridad) el agua
ha subido una altura de 40 cm. Teniendo en cuenta que los poros
tienen forma cilíndrica y el agua moja perfectamente al
suelo, determina el diámetro de los capilares.

3.- Entre dos láminas verticales y paralelas que
se encuentran entre sí a una distancia de 0,25mm hay un
líquido. Hallar la densidad del mismo sí sabemos
que se eleva entre las láminas 3,1cm, mojando al
sólido perfectamente si

4.- ¿ A qué equivale el coeficiente de
tensión superficial de la gasolina si la altura a que se
eleva en un tubo vertical, cuyo diámetro interior es de
0,4 mm es de 3cm. El mojado es total y r gasolina = 700 kg/m3.

5.- Hasta que altura se elevará el Benzol en un
tubo capilar cuyo diámetro interior es de 1mm, si
consideramos que el benzol moja perfectamente.

.
r benzol = 880 kg/m3

6.- Qué diámetro máximo pueden
tener los poros de la mecha de una hornilla de petróleo para que este último suba
desde el fondo del depósito hasta la mecha de la hornilla
(h=10cm). Considere que los poros son tubos cilíndricos y
que el
petróleo moja perfectamente.

a petróleo =
0,03 N/m.
petróleo = 780 kg/m3

7.- Calcule la energía cinética media de
las moléculas de un gas cualquiera a 50C de temperatura.
¿ Se puede decir de un gas cualquiera? ¿Por
qué? ¿ Cuál es la energía
cinética total de 2 moles de gas a esa misma
temperatura?.

8.- En un recipiente de 10 l de capacidad hay 10 g de
oxígeno a la presión de 680 mm de Hg. Halle la
cantidad de moléculas que hay en el recipiente.

9.- ¿ Qué temperatura tienen 2
.10-3 kg de N2 que ocupan un volumen de 320
. 10-3 m3 a la presión

de 2. 105 Pa.

10- Un recipiente contiene 40 l de gas ideal a la
presión de 1,52. 105 Pa y a la temperatura de
50C. ¿
Cuál será la presión si el volumen aumenta
hasta 400 l y la temperatura se eleva a 225 C ?.

11- En la teoría cinética molecular
suponemos que hay un gran número de moléculas en un
gas. Los gases reales a bajas temperaturas se comportan como un
gas ideal. ¿Son contradictorios estos enunciados? Si no lo
son ¿Qué conclusión puede sacar de
ellos?

12- Explique con palabras por qué el calor
específico a presión constante es mayor que el
calor específico a volumen constante.

13- Analicemos el siguiente mapa conceptual.

A partir del mismo explique: 1) ¿Por qué i
= 3 para una molécula monoatómica?

2) Cuándo i = 5 y cuándo i = 7 para una
molécula de dos ó más
átomos?

Tarjeta de
estudio No. 2. Tema: Teoría Cinético
Molecular

Actividad: Seminario del
Tema: Teoría Cinético Molecular (TCM).
Líquidos y gases.

Objetivo: Aplicar los postulados de la TCM y las
leyes estudiadas en la solución de diferentes
problemas.

Actividades a ejecutar.

1. 

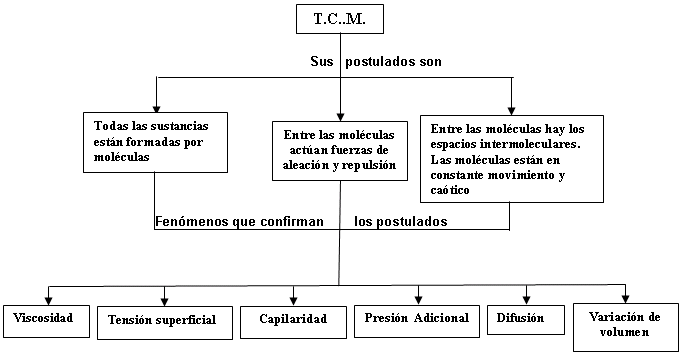
2. Analicemos el siguiente mapa conceptual sobre la
   teoría cinética – molecular y completa el
   mismo planteando las leyes que explican cada fenómeno y
   relaciónelo con el postulado al cual le dan
   cumplimiento.
3. En la teoría cinética molecular
   suponemos que hay un gran número de moléculas en
   un gas. Los gases reales a bajas temperaturas se comportan como
   un gas ideal. ¿Son contradictorios estos enunciados? Si
   no lo son ¿ Qué conclusión puede sacar de
   ellos?.
4. Explique a partir de los postulados de la
   teoría cinética – molecular él por
   qué se roturan los terrenos antes de ser
   sembrados.
5. Explique con palabras por qué el calor
   específico a presión constante es mayor que el
   calor específico a volumen constante.
6. En un tubo de vidrio de paredes limpias vemos que al
   verter agua el menisco que se forma es cóncavo, mientras
   que si las paredes del tubo están cubiertas de parafina
   el menisco será convexo. Explica a que se debe
   esto.

Tarjeta
de estudio No. 3. Tema: Termodinámica

Tema:
Termodinámica

Temática: Objetivos de la
termodinámica. Sistema termodinámico. Equilibrio
termodinámico. Coordenadas termodinámicas
(Presión, Volumen y Temperatura). Procesos
reversibles e irreversibles. Primer principio de la
termodinámica. Trabajo
realizado al cambiar de volumen un gas. Proceso
adiabático. Calor intercambiado en algunos procesos
termodinámicos. Variación de energía
interna. Segundo principio de la Termodinámica. Eficiencia.
Enunciado según Clausius y según Kelvin.
Desigualdad de Clausius. Ciclo de Carnot. Motor y
refrigerador de Carnot. Entropía. Cálculo de
la variación de la entropía. Principio de aumento
de la entropía.

Objetivos

1. Realizar cálculos de Q, W y intercambiados en
   procesos termodinámicos (isocóricos,
   isobáricos, isotérmicos y adiabáticos)
   aplicando al primer principio de la termodinámica y las
   expresiones correspondientes a cada magnitud.
2. Interpretar y aplicar el primero y el segundo
   principio de la Termodinámica en el análisis de
   ciclos y de procesos termodinámicos, así como
   establecer relaciones entre ellos.
3. Calcular Qneto , Wneto y
   eficiencia en ciclos termodinámicos, estableciendo
   diferencias entre los ciclos motor y refrigerador, así
   como la variación de entropía para diferentes
   procesos, reversibles e irreversibles.

Información teórica
básica

• Un proceso termodinámico tiene lugar cuando
  por variación de las coordenadas termodinámicas
  macroscópicas (P, V y T) el sistema pasa de un estado de
  equilibrio termodinámico a otro en un intervalo de
  tiempo dado. Un sistema se encuentra en estado de equilibrio
  termodinámico cuando el valor de las coordenadas
  termodinámicas (P, V y T) son las mismas para toda la
  masa del sistema.
• Cuando un sistema termodinámico va de un
  estado de equilibrio termodinámico inicial a otro final,
  de forma lenta, pasando por estados intermedios consecutivos de
  equilibrio termodinámico, lo cual puede ser representado
  en un plano termodinámico como una línea continua
  y puede regresar a su estado de equilibrio termodinámico
  inicial, siguiendo el mismo trayecto que recorrió
  inicialmente, es decir pasando por los mismos estados
  intermedios de equilibrio termodinámico, de forma tal
  que al llegar al estado inicial, las condiciones del sistema y
  de los alrededores sean las mismas que existían antes de
  ocurrir el proceso se dice que el proceso es reversible.
  Si alguna de estas condiciones no se cumplen, entonces el
  proceso será irreversible.
• Grados de libertad (i)
  son las posibilidades de movimiento independiente que tiene una
  partícula en el espacio a las cuales se halla asociado
  una determinada forma de energía. El valor promedio que
  le corresponde a cada uno de esos términos
  independientes es igual a ½kT, es decir depende
  únicamente de la temperatura y está distribuida
  en partes iguales y se conoce como Principio de
  Equipartición de la Energía. En el caso de un gas
  ideal monoatómico a las moléculas sólo
  está asociada energía cinética
  traslacional, ya que las dimensiones de estas son despreciables
  (KROT = 0) y no existen fuerzas de
  interacción entre ellas (U = 0); por lo tanto K = 3/2 k
  T lo que implica que la U = 3/2 kT. Esto se corresponde con el
  hecho de que i = 3.
• Conocemos que CP = CV
  + R y que la ΔEINT
  = n CV ΔT o tambiιn
  ΔU =i/2nRΔT, por lo que,
• CV = i/2 R y CP = i+2/2
  R.
• Recordemos las expresiones correspondientes a cada
  proceso, para el cálculo de el calor intercambiado (Q),
  la variación de energía interna (

) y el trabajo
realizado (W).

NOTA: Los valores de Q y
W son absolutos en todas las expresiones..

Primera ley de la termodinámica Q = + W

g =
CP/CV CP = CV +
R

• La cantidad de calor intercambiada entre el sistema y
  los alrededores se considerará positiva si el sistema
  absorbe calor y negativa si cede, la variación de
  energía interna será positiva si aumenta la
  temperatura del sistema al pasar de un estado de equilibrio
  termodinámico a otro y negativa si disminuye la
  temperatura (recuerde que la energía interna es una
  función de estado únicamente dependiente de la
  temperatura) y el trabajo se considerará como positivo
  si es el sistema quien lo realiza sobre los alrededores, lo que
  implica un aumento de volumen y negativo en caso
  contrario.
• Un ciclo termodinámico está integrado
  por una serie de procesos consecutivos, de forma tal que
  el estado de
  equilibrio termodinámico final del sistema coincide con
  el inicial, por lo cual

= 0 (la temperatura final y la inicial es la misma) y
para el ciclo el Qneto = Wneto.

• La eficiencia para un motor térmico
  (h ) siempre será menor que
  la unidad y se calcula como:

h =

• La eficiencia para un refrigerador (K) se calcula
  como: K=
• El ciclo motor es recorrido en el mismo sentido en
  que se mueven las agujas del reloj, siendo el WNETO
  > 0, mientras que el ciclo
  refrigerador es recorrido en sentido contrario al que se mueven
  las agujas del reloj y el WNETO < 0. Tenga en cuenta que el WNETO
  es numéricamente igual al área dentro del
  ciclo.
• El ciclo de Carnot consta de dos procesos
  adiabáticos y dos isotérmicos, todos reversibles,
  por lo que sólo hay intercambio de calor entre el
  sistema y los alrededores en los procesos isotérmicos, y
  el sistema opera entre dos temperaturas solamente. La
  eficiencia de este ciclo se puede calcular mediante la
  siguiente expresión.

Para un motor de Carnot h =
= 1
–TCED/ TABS

Para un refrigerador de Carnot K =

• El teorema de Carnot plantea que la eficiencia de
  cualquier máquina térmica que opere entre dos
  temperaturas específicas, nunca podrá superar la
  eficiencia de una máquina térmica de Carnot que
  funcione entre las mismas dos temperaturas.

• Para cualquier ciclo reversible § dQ/T = 0, lo
  que quiere decir que se evalúa el ciclo para una
  trayectoria cerrada, terminando en el mismo punto en que se
  inició la observación. La expresión anterior
  nos indica que la variable dQ/T es una función de
  estado, ya que no depende de la trayectoria, sino de valor de
  las coordenadas para los puntos de inicio y fin de la
  observación. Esta variable la denominamos
  entropía (S) siendo ∆S = , la que se expresa en el SI en J/K y
  en el sistema inglés en atm-l/K.
• El cálculo de ∆S para los diferentes
  procesos reversibles estudiados es:

Proceso isobárico ∆S = Sf
– Si = = = n CPln Tf /
Ti

Proceso Isocórico ∆S = n CV
lnTf /Ti

Proceso isotérmico ∆S = nRln
Vf /Vi

Proceso adiabático ∆S = 0

Proceso irreversible. Se calcula a través de
procesos reversibles.

• La desigualdad de Clausius se expresa como §
  dQ/T ³ 0 siendo igual a cero
  para procesos reversibles y mayor que cero para los
  irreversibles. En un proceso reversible cualquiera en todo
  momento la temperatura del sistema es igual a la de los
  alrededores, con el que intercambia calor y el dQ absorbido por
  el sistema es igual al cedido por los alrededores, de
  ahí que se cumpla que: ∆SSIST = –
  ∆SAlRED es decir que la ∆S del sistema
  cuando realiza un proceso reversible puede tener cualquier
  valor y cualquier signo pero la de los alrededores
  tendrá el mismo valor y signo contrario.
• Cuando el proceso que se realiza es irreversible,
  ∆SSIST + ∆SAlRED › 0,
  es decir

que ∆SSIST puede ser positivo, negativo
e incluso valer cero pero el ∆SAlRED

tendrá un valor tal que la suma será mayor
que cero.

Ejercicios Resueltos

El gráfico de P vs. V representa tres
procesos

experimentados por un gas cuyo comportamiento es ideal.
La temperatura en el punto A es de 600 K, la

presión de 16 atm y el volumen de 1 litro y en el
punto b el volumen es de 4 l. Uno de los procesos ab o

ca es isotérmico y el otro adiabático y la
relación entre los calores específicos a
presión y volumen es de 1.5.

Determine:

a)¿Cuál de los procesos es el
isotérmico y cual es el adiabático?
Explique.

b) La presión y la temperatura en los puntos b y
c.

c) El volumen en c.

d) El calor intercambiado en cada proceso.

e) El trabajo realizado en cada proceso.

f) La variación de energía en cada
proceso.

R = 0,082 atm l/mol K

g =1,5

1. El proceso CA es isotérmico y el AB es
   adiabático pues este último tiene mayor pendiente
   que el isotérmico, por lo que la temperatura en C
   será la misma que en A.
2. Como el proceso ab es adiabático podemos
   plantear que

PaVag
=PbVbg Þ 16 (1)1,5=
Pb(4)1,5Þ 16 = (4/1)1,5 Þ 16 = Pb(8) Þ Pb = 2
atm.

Para calcular la temperatura en b planteamos lo cual es
válido entre dos estados de equilibrio
termodinámico cualquiera.

c) Para hallar Vc, como el proceso bc es
isobárico, la Pb = Pc, por lo que:
o como el
proceso es isotérmico Ta = Tc, por lo que:
PaVa = Pc Vc y
sustituyendo valores obtenemos por una u otra expresión
que

Vc =8 l

d) Cálculo del calor intercambiado en cada
proceso.

– Proceso ab (adiabático) Qab =
0

– Proceso bc (isobárico) Qbc = n
CPD T, debemos entonces
hallar el valor de n y de CP.

El valor de n (# de moles) se calcula aplicando la
ecuación de estado para cualquiera de los puntos (a, b
ó c).

Para calcular CP simultaneamos las
expresiones Cp=Cv+R y g = donde g
=CP/CP -R

1,5 = CP/CP –0,08 por lo que
1,5 (CP –0,08) = CP donde
CP = 0,24 atm l/mol K

Y sustituyendo en cualquiera de las dos expresiones
obtenemos que Cv=0,16 atm l/mol
K.

Qbc = n CPD T =1/3 mol 0,24 atm l/mol K(600K- 300K)
donde QBC= 24 atm l

Proceso CA (isotérmico) Q = W = nRT
lnVa/Vc donde Qca =1/3 mol 0,08
atm l/mol K 600 K ln(1/8)

Qca =16 atm l (ln 1–ln 8) donde
Qca= – 33,28 atm l

El signo menos indica que el sistema cede calor a los
alrededores.

e) El trabajo realizado en cada proceso

– Proceso ab (adiabático) W=nCVD t ó W=PbVb
–PaVa/g –
1 donde Wab= – 16 atm

• Proceso bc (isobárico) W=PD V =nRD t donde
  Wbc= – 8 atm l

• Proceso ca (isotérmico) Wca=
  – Qca= 33,28 atm l

f) La variación de energía interna en cada
uno de los procesos.

• Proceso ab (adiabático)

= W = -16 atm l

• Proceso bc (isobárico)

= nCvD T o
aplicando la primera ley de la termodinámica

bc = Qbc – Wbc
Þ bc = 24 atm l – 8 atm
l donde BC =16 atm l

• Proceso ca (isotérmico)

= 0 (ya que la temperatura es
constante).

2-

Halle el trabajo neto en el ciclo abcda mostrado en la
figura, conociendo que la eficiencia de un

refrigerador que funciona siguiendo este ciclo es K =
1,5. El proceso CD es
adiabático y el

área bajo el proceso BC es igual a 3739,5
J.

Otros datos:

V (m3) TA = 300K g = 1,5

TB = 200K n = 1 mol

Nos piden calcular el trabajo neto, el cual podemos
hallar mediante la expresión K = por lo que debemos señalar en que
procesos se absorbe calor.

• Proceso ab (Isocórico) disminuye la
  energía interna ya que TB < TA, siendo < 0 y como W=0, se cede calor por el sistema
  (Q=)
• Proceso BC (Isobárico) aumenta la
  energía interna, ya que Tc> Tb, siendo > 0 y el trabajo es realizado por el
  sistema, siendo W ‹ 0, por lo que el sistema absorbe
  calor (Q = + W)
• Proceso CD (adiabático) Q = 0 (no intercambia
  calor el sistema con los alrededores)
• Proceso DA (isobárico) disminuye la
  energía interna, ya que Ta < Td y se realiza trabajo sobre
  el sistema (W › 0), por lo que el sistema cede
  calor.
• De acuerdo con el análisis realizado
  sólo se absorbe calor en el proceso BC, siendo
  Qbc= nCp (Tc –
  Tb) y como no conocemos Tc y
  Cp debemos primero calcularlos.

Para calcular CP simultaneamos las
expresiones:

Ahora estamos en posibilidades de calcular el
Qabs, donde

3- Un motor que trabaja entre dos fuentes a 600
K y 300 K y que recibe 600 J de la fuente a 600 K, entregando 300
J a la fuente a 300 K. El trabajo obtenido de este motor se le
entrega a un refrigerador que trabaja entre dos fuentes a 900 K y
400 K y absorbe 480 J de energía.

1. ¿Qué calor entregará este
   refrigerador?
2. ¿Cuál es la eficiencia del
   motor?
3. ¿Cuál es la eficiencia del
   refrigerador?

Conocemos que Qneto=Wneto, pues
para un ciclo =0 y como

Qneto=Qab + Qcedpor lo que:
Wneto = 600 J – 300 J Þ

Observe que el calor cedido es negativo.

Es decir que el refrigerador recibe un trabajo
equivalente a 300 J para funcionar y como para éste
también se cumple que el Wneto =Qabs
+ Qced Þ
-Qced = Qabs, – Wneto pero como
en este caso el trabajo es realizado sobre el sistema tendremos
que:

-Qced = 480 J + 300 J Þ (El signo menos indica que el sistema
cede calor a los alrededores)

Calculemos ahora la eficiencia del motor h = ó

Y la eficiencia del refrigerador será K = –

P (Pa)

4-

Un mol de gas ideal experimenta el ciclo representado,
siendo el área bajo el proceso 2-3 igual a 2098,5 J,
g = 1,4 y T3 = 300
K.

Halle: a) La eficiencia del ciclo

b) La variación de entropía en cada
proceso.

Nota: El proceso 2-3 es adiabático
y el 3-1 es isotérmico.

Atendiendo al ciclo representado reconocemos que
corresponde con un motor, ya que es recorrido en el sentido en
que se mueven las manecillas del reloj, por lo que:

W
neto = Qneto = Qabs –
Qced, por lo que . Debemos definir en qué procesos se absorbe y
en cuales se cede calor teniendo en cuenta que en el proceso 2-3
no hay intercambio de calor entre el sistema y los alrededores
pues es adiabático (Q2–3 = 0).

En el proceso 1-2 se absorbe calor pues aumenta la
temperatura lo que implica que aumente la energía interna
y además el sistema realiza trabajo sobre los alrededores
y como Q =`+ W, si W es negativo y es positiva, Q será positiva;
mientras que en el proceso 3-1 se cede calor, pues la
energía interna disminuye ( es negativa) ya que disminuye la
temperatura y el trabajo es realizado sobre el sistema pues
disminuye el volumen (W es positivo).

Q1-2 = n cp (T2 –
T1) y Q3–1= nRT ln De estas expresiones se
deduce que es necesario conocer los valores de Cp,
Cv, T2 y T1.

Para calcular Cp, y Cv, planteamos
que
Cp = CV+R simultaneando ambas expresiones
tendremos que:
sustituyendo valores 1,4 Cv – Cv
=

8,31 J/molKÞ
Cp= Cv + R Þ

Para calcular T2 y T1

T1= T3 = 300 K, por ser el proceso
3-1 isotérmico, también tenemos que el área
bajo el proceso 2-3 es de 2098,5 J, lo que será
numéricamente igual al trabajo.

W2-3 = -n Cv (T3
– T2) Þ
T2 = T3 +

Calculemos ahora la eficiencia h = Q12 +
Q31/Q12 siendo

h = n
CP(T2- T1) – nRT
lnV1/V3 ∕
nCP(T2-T1) y sustituyendo
valores obtenemos que: o

El signo negativo para Q3-1 nos indica que
este calor es cedido.

1. calculemos ahora la variación de
   entropía (D S) para cada
   proceso

D S1-2 = n
cp lnT2/T1Þ D
S1-2 = l mol 29 J/mol K ln 400,9K/300K Þ

ya que D S = y d Q2-3 = 0
por ser el proceso adiabático

D S3-1 = nR ln

1. ¿Qué variación de
   entropía sufre el universo
   cuando se le añade un cubito de hielo a un vaso de agua
   a temperatura ambiente?
   Considere que el vaso de agua no intercambia calor con el
   exterior. El vaso contiene 300g de agua y el cubito de hielo
   tiene aproximadamente 80g. Considere además que el calor
   específico del vidrio es despreciable y la temperatura
   ambiente es de 30

C

Datos

CH2O = 1 cal / gC

LH2O= 80 cal/g D
SUNIV = D SSIST
+ D SALRED

m H2O= 300g

m H2O= 80 g D
Salred. = 0 (por estar al sistema
térmicamente

Tamb =30C =303K aislado)

D SUNIV =?
D SUNIV = D SSIST = D
SH2O + D
SHIELO

Pero D S = y como el sistema
está térmicamente aislado

QABS – QCED = 0 Þ QABS =
QCED

El hielo por encontrarse a una menor temperatura
será el que absorbe el calor y el agua cede, siendo la
temperatura final la de equilibrio térmico, la que
será mayor de 0° C, por lo
que el hielo se fundirá y después los 80g de agua
elevarán su temperatura hasta lograr el equilibrio
térmico. MHIEKO L + m c D t = – mH »O cD t

MHIELO L + m c (t – 0° C) = – mH »O C (t –
30° C)

80g. 80 cal/g + 80g 1 cal/g° C (t – 0° C)
= – [ 300g. 1 cal /g° C (t- 30°
C)]

6400 cal + 80 t cal/g = – 300 t cal/g + 9000
cal.

380t = 2600 Þ
o

D SH2O =
Toò TdQ/T
Þ D
SH2O = Toò TmCdt/T Þ D
SH2O = mClnT/TAMB Þ D
SH2O = mc (lnT – lnTAMB)

D SH2O = 300 g 1
cal/gK (ln 279,84 – ln 303) Þ D
SH2O =300cal/k (5,63 –5,71) donde

Preguntas y problemas propuestos.

1-

Dos moles de un gas cuyo comportamiento es Ideal para el
cual Cv = 12, 46J/molK efectúan los procesos
descritos en el plano P-V.

El proceso bc es una compresión
isotérmica. Calcule para cada proceso Q, y W.

2- Un mol de gas perfecto se introduce en una vasija
cerrada mediante un émbolo que mantiene la presión
atmosférica sobre el gas. Este se calienta hasta que su
temperatura se eleva a 127C, duplicando su volumen.

1. Trace un diagrama PV
   para este proceso.
2. Calcule Q, y W.
3. Especifique si es el sistema o los alrededores quien
   hace trabajo.
4. ¿Qué trabajo se habrá realizado
   si la presión externa es de 0,5 atm en lugar de la
   atmosférica normal?

3-

P Un mol de gas ideal efectúa el ciclo mostrado
en la figura. Si el área bajo el proceso 3 – 1 es
igual

Isoterma a 1662 J, g =
y la eficiencia
0,5. Halle:

1 3 a) El sentido en que se recorre el ciclo.

b) Cp y CV.

c) D t entre 1 y 3

0 V d) Q 1-2

e) W 2-3

f) Q 2-3

4- P(Pa) Dos moles de un gas ideal para el cual
CV=12,97 J/mol K

b efectúan los procesos señalados en la
gráfica. El proceso bc

es una expansión isotérmica.
Calcule:

a) Q, y W para cada proceso.

b) Eficiencia del ciclo.

103250 a c

0 8 16 V (10-3) m3

5.- Complete el siguiente mapa conceptual.

6.- Un motor que funciona entre dos focos a 800 K y 300
K absorbe 4800 J del foco caliente, con una eficiencia del 62,5
%. Si el trabajo que entrega este motor se le suministra a
refrigeradores reversibles que entregan 900 J a un foco a 600
K.

1. ¿Cuántos refrigeradores de K = 2
   podrán funcionar?
2. Construya el gráfico ilustrativo de este
   problema.

7.- Una máquina de Carnot tiene una eficiencia
del 22 % y opera entre dos depósitos de calor cuya
temperatura difiere en 75 0C. Halle las temperaturas
de los depósitos.

8.- P (atm) Medio mol de gas cuyo comportamiento es
ideal realiza el ciclo irreversible mostrado,

siendo Cv = 2 R. Dicho ciclo tiene una
eficiencia del 10 %. Si en el proceso irreversible cede calor
solamente:

1. Calcule las temperaturas en 1, 2 y 3.
2. Halle el calor absorbido en el ciclo.
3. Halle el calor neto y el trabajo neto.
4. Halle el calor cedido en el proceso
   irreversible.

e) Calcule la variación de entropía del
sistema en el proceso 3-1 y en el proceso 1-3 . Compare en cada
caso como debe ser D S en los
alrededores y analizar el principio de aumento de la
entropía.

9.- Complete el siguiente mapa
conceptual.

10 – Un kilogramo de agua a una temperatura de 7
0C es mezclado con 2 kg de agua a 37C de temperatura
en un recipiente térmicamente aislado. Encuentre la
variación de entropía del Universo. C= l
kcal/mol K

11-Se tiene un mol de un gas ocupando 6 l a la
presión de 2 atm. Si se realiza una transformación
isocora adquiriendo una presión de 3,5 atm. Determine la
variación de entropía si CV= 0,128 atm
l/mol K

12-

P (Pa) En el ciclo de la figura halle la
variación de 1 2 entropía de 3 a 4 y la eficiencia,
suponiendo 520,12 que el gas que realiza el ciclo es ideal y que
el proceso 3 4 es isotérmico.

R = 8,31 J/mol K

405,39 3

0 1 3 V(m3)

13.-

El grafico PV dado representa un proceso 1 reversible de
un motor térmico. El cambio de
entropía del sistema al pasar del estado

a al b a lo largo de la trayectoria 1 es de 2 0,60 J/K .
¿ Cuál es el cambio de entropía al pasar
:

a) del estado a al b según la trayectoria 2
?

b) del estado b al a según la trayectoria 2
?

14-Construya un mapa conceptual atendiendo al siguiente
listado de proposiciones conceptuales, frases y/o palabras
enlace.

15- Explique por qué disminuye la temperatura de
un gas en una expansión adiabática.

16- Si el aire caliente se
eleva ¿Por qué esta mas frío el aire en la
cumbre de una montaña que cerca del nivel del
mar?

17- Dos muestras de un gas que inicialmente están
a la misma temperatura y presión se comprimen desde un
volumen V hasta V/2, una isotérmicamente y la otra
adiabáticamente. ¿En qué muestra es mayor
la presión final? ¿Cambia la entropía del
gas en alguno de los procesos? Explique ambas
respuestas.

18- Explique a partir de la primera ley de la
termodinámica qué pasa con el calor intercambiado
en un proceso isotérmico entre el sistema y los
alrededores.

19- ¿Qué requisitos debe cumplir un
sistema para que esté en equilibrio
termodinámico?

20- ¿Puede ser la eficiencia de un motor mayor
que la unidad? Explique.

21- ¿Cómo puede explicar que al realizarse
un proceso irreversible, un sistema estando aislado, aumente la
entropía?

22- ¿Cuál será el valor de la
para un
proceso isotérmico reversible? ¿Cuál para un
proceso irreversible donde la temperatura inicial sea igual que
la final?

Bibliografía

1. Ausubel, David P. Psicología Educativa. Un punto de vista
   cognoscitivo. Editorial Trillas Méjico Décima
   edición Mayo de 1997.
2. Galperin, P. Ya. Desarrollo
   de la investigación de la formación de
   las acciones
   mentales. En la colección Ciencias
   Pedagógicas de la URSS. Academia de Ciencias
   Pedagógicas de la RSFSR.1959.
3. García Martínez, Andrés.
   "Física
   General Aplicada. Novedosa Concepción para la enseñanza dela Física en Ciencias
   Técnicas" Tesis en
   opción al grado científico de Dr en
   CienciasPedagógicas Ciudad de la Habana
   1997.
4. Halliday D., Resnick R. y Kenneth S. K.
   Física. Volumen I tomos I y II. Cuarta edición.
   Editorial Felix Varela. Ciudad de la Habana. Cuba.
   2003
5. Leontiev, A. N. Actividad, conciencia y
   personalidad. Editorial Pueblo y Educación. La Habana. 1981.
6. Moreira, Marco Antonio. Mapas
   Conceptuales. Instituto de Física Universidad
   Federal de Río Grande del Sur Puerto Alegre.
   1990.
7. Novak, Joseph y Gowin D. Bob. Aprendiendo a aprender.
   Ediciones Martínez Roca SA. España.
   1988.
8. Novak, Joseph D. Concept Maps and Vee Diagrams two
   metacognitive tools to facilitate meaningful learning.
   Instructional Science. Kluwer Academic Publishers. Dordrecht
   Printed in the Netherlands. Pag. 29-52 1990
9. Ontoria Peña, Antonio. Mapas
   Conceptuales. Una técnica para aprender. Ediciones
   Narcea SA. Madrid.
   l992.
10. Pérez de Prado Santa Maria, Antonio. Nueva
    propuesta de perfeccionamiento de la Física I para
    estudiantes de Ingeniería Agronómica. Tesis de
    Maestría. Matanzas. 1999
11. Pérez de Prado Santa Maria, Antonio. Tarjetas de
    Estudio de Física I para estudiantes de
    Ingeniería Agronómica. Universidad de Matanzas
    "Camilo Cienfuegos". Cuba.1995.
12. Pérez de Prado Santa Maria, Antonio. Tarjetas
    de Estudio de Fí
    Partes: 1, 2