Partes: 1, 2

Solución

Aplicando la segunda ley de Kirchhoff a las mallas KLMNK y JKNPJ

Estas dos ecuaciones son el modelos matemáticos, ahora vamos a encontrar las corrientes.

Aplicando la transformada de Laplace del sistema y utilizando las condiciones iniciales I1(0)=I2(0)=0

-5i1 - {si1 - I1(0)}+ 2{si2-I2(0)} + 10i2= 0

{si1 - I1(0)} + 20i1 + 15i2 = 55/s

(s + 5)i1 - (2s + 10)i2 = 0.............Ecuación (1)

(s + 20)i1 + 15 i2 = 55/s............ Ecuación (2)

Si factorizamos la ecuación 1

(s + 5)i1- 2( s + 5)i2=0

(s + 5)(i1-2i2) = 0

I1- 2i2 = 0 entonces i1=2i2 y sustituyendo en la ecuación 2 nos queda

Si aplicamos la transformada inversa de Laplace

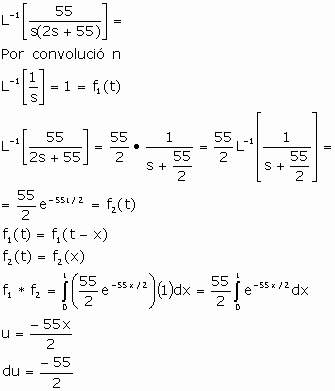
Entonces

Ejemplo 2

Obtener función de transferencia del siguiente diagrama

Solución

El diagrama es como la siguiente figura y a la vez se transforma como muestra en la figura b

De la malla I

E i (s) = Z 1I + Z2I 2 .......(1)

De la malla 2

-Z2I1+Z3 I2 + Z4I2=0 .. ....(2)

De la malla 3

E o (s)= Z4 I2.................(3)

Por división de corriente sabemos que

Ahora sustituimos la ecuación (5) en la ecuación (1) y nos queda

La ecuación (6) la sustituimos en la ecuación (3) y nos queda

Para hallar la función de transferencia dividimos Eo (s)/ Ei (s)

Aquí sustituimos Z2=1/C1s, Z4=1/C2s, Z1=R1 y Z3 = R2, la función de transferencia y nos queda

BIBLIOGRAFÍA

Ogata, Katsuhiko. Ingeniería de control moderna. Cuarta edición, Madrid, Pearson

Prentice-Hall, 2003, 965 pp.

Spiegel, Murray R. Transformadas de Laplace. Primera edición, México, McGraw- Hill, 1991, 261 pp.

 

BIBLIOGRAFIA DEL AUTOR

Alejandro López Ham,

Nació en Tula de Allende Hidalgo es Ing. en electrónica y de comunicaciones, estudio en la Universidad Tecnológica de México

México, 13 de septiembre de 2007