Muestreo de aceptación (página 2)

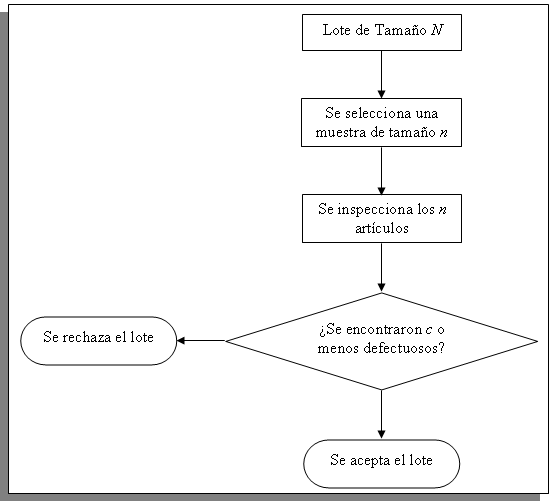
Figura 1. Esquema de un plan de muestreo de
aceptación por atributos (N, n, c).

2. Cero inspección (aceptar o mandar el lote
   sin inspección). Esta alternativa es adecuada cuando
   el proceso
   que fabricó el lote ha demostrado cumplir holgadamente
   los niveles de calidad
   acordados entre el cliente y
   el proveedor (que seria el caso de procesos
   estables y con un buen Cpk, o procesos en los que
   se han hecho inspección previa). También se
   aplica cero inspección cuando la pérdida global
   causada por las unidades defectuosas es pequeña con el
   costo del
   muestreo.

   Se pensaría que la inspección al 100%
   aunque costosa es una buena estrategia
   para garantizar calidad, pero esto no es correcto, debido a
   que en la inspección al 100% se puede caer en la
   monotonía, en mayores errores de inspección y
   en ocasiones el producto
   de daña. Incluso hay casos en los que debido a los
   primeros dos problemas
   de la inspección al 100% se tiene como política que las unidades se
   inspeccionen doble vez (inspección 200%)

3. Inspección al 100%. Consiste en revisar
   todos los artículos del lote y quitar los que no cumplen
   con las características da calidad establecidas. Los que
   no cumplen podrían ser devueltos al proveedor,
   reprocesarlos o desecharlos. La inspección al 100% se
   utiliza en aquellos casos en que los productos
   son de alto riesgo y si
   pasan defectuosos puede causar gran perdida económica.
   También es útil cuando la capacidad del proceso
   fabricante del lote es inadecuada para cumplir las
   especificaciones.
4. Muestreo de aceptación
   (inspección por muestras). Esta opción es
   útil cuando se tiene una o varias muestra de las
   siguientes situaciones:

• Cuando la inspección se hace con pruebas
  destructivas (como pruebas de tensión y resistencia), es indispensable la
  inspección por muestras, de lo contrario todos los
  productos serían destruidos con las
  pruebas.
• Cuando el costo de la inspección al 100% es
  demasiado alto comparado con el costo de pasar unidades
  defectuosas.
• En los casos en los que la inspección al
  100% no es técnicamente posible o se requiere mucho
  tiempo
  para llevarlo a cabo.
• Cuando el lote lo forman gran cantidad de
  artículos que habría que inspeccionar y la
  probabilidad
  de error en la inspección es suficientemente alta, de
  manera que la inspección al 100% podría dejar
  pasar más unidades defectuosas que un plan de
  muestreo.
• En situaciones donde históricamente el
  vendedor ha tenido excelentes niveles de calidad y se desea
  una reducción en la cantidad de inspección,
  pero la capacidad del proceso no es suficientemente buena
  como para no inspeccionar.
• Cuando es necesario asegurar la confiabilidad del
  producto, aunque la capacidad del proceso fabricante del lote
  sea satisfactoria.

VENTAJAS Y DESVENTAJAS DEL MUESTREO DE
ACEPTACIÓN

El muestreo de aceptación respecto a la
inspección al 100% tiene las siguientes
ventajas:

1. Tiene menor costo porque se inspecciona menos, a
   pesar de algunos costos
   adicionales generados por la planificación y administración de los planes de
   muestreo.
2. Requiere de menos personal en las
   actividades de inspección, simplificando con ello
   el trabajo
   de coordinación y reduciendo los
   costos.
3. El producto sufre menos daño
   al haber menos manipulación.
4. Es aplicable en pruebas destructivas.
5. A menudo reduce el error de inspección y la
   monotonía.
6. El rechazo de lotes completos por la existencia de
   artículos defectuosos proporciona una motivación al fabricante del lote para
   que mejore su calidad.

El muestreo de aceptación presenta algunas
desventajas, como las siguientes:

1. Hay cierto riesgo de aceptar lotes malos y rechazar
   buenos, aunque en un plan de muestreo de aceptación
   están previstos y cuantificados estos riesgos.
2. Proporciona menos información acerca del nivel de calidad
   del producto o de su proceso de fabricación. Aunque bien
   utilizada, la información obtenida puede ser
   suficiente.
3. Se requiere más tiempo y conocimiento
   para planificar y documentar el muestreo, mientras la
   inspección al 100% no. Esto tal vez no sea una
   desventaja, ya que la planificación genera otros efectos
   positivos, como mayor conciencia
   de los niveles de calidad exigidos por el cliente.

Las ventajas que tiene el muestreo de aceptación
sobre la inspección al 100%, lo hacen una herramienta
importante ahí donde haya condiciones para aplicarlo. En
este sentido, muchas empresas, sobre
todo pequeñas y medianas, aplican inspección al
100% más por tradición y desconocimiento que por
una razón fundamentada. Por lo que un paso importante
sería lograr que se aplicara muestreo de aceptación
en aquellos casos que así lo ameriten.

Por otro lado, no es raro escuchar de algunos expertos
en calidad que el muestreo de aceptación ya no debe
usarse, que es obsoleto, ya que no es un concepto valido.
Al respecto nuestra posición es que: se debe hacer
énfasis en mejorar la calidad y corregir de fondo las
causas de la mala calidad y la baja competitividad
aplicando herramientas
estadísticas, diseño
de experimentos,
proyectos
Seis Sigma,
etcétera; pero mientras tanto no se tengan niveles
óptimos de calidad, seguirá siendo necesario
aplicar estrategias de
contención como lo es el muestreo de aceptación. De
aquí que en muchas empresas donde los niveles de calidad
no son satisfactorios, el muestreo de aceptación debe
verse como una herramienta temporal y útil.

TIPOS
DE PLANES DE MUESTREO

Los planes de muestreo de aceptación son de dos
tipos: por atributos y por variables.

En los planes por variables se toma una muestra
aleatoria del lote y a cada unidad de la muestra de la mide una
características de calidad de tipo continuo (longitud,
peso, etc.).

Con las mediciones se calcula un estadístico, que
generalmente está en función de
la media, la desviación estándar muestral y las
especificaciones, y dependiendo del valor de este
estadístico al compararlo con un valor permisible, se
aceptará o rechazará todo el lote. En la
sección "Muestreo de aceptación por variables" de
este trabajo se
verá estos tipos de planes.

En los planes por atributos se extrae
aleatoriamente una muestra de un lote y cada pieza de la muestra
es clasificada de acuerdo a ciertos atributos como aceptable o
defectuosa. Si el número de piezas que se encuentran
defectuosas es menor o igual que un cierto número
predefinido, entonces el lote es aceptado; en caso de que sea
mayor, entonces el lote es rechazado. Algunos de los planes por
atributos son: simple, doble y múltiple.

En general los planes más usuales son los de
atributos, a pesar de que con los planes por variables se
requieren menor tamaño de muestra para lograr los mismos
niveles de seguridad. Esta
aparente contradicción se debe a la tradición o a
razones más validas, por ejemplo a que en los planes por
atributos se pueden combinar varias características de
calidad en un solo plan, mientras que en los planes por variables
hay que diseñar un plan para cada característica de
calidad. Además en ocasiones las mediciones en los planes
por variables son más costosas. De esta manera se debe
procurar que la decisión de que tipo de plan utilizar se
fundamente en un análisis detallada de los costos que
implica cada plan, así como la facilidad de llevarlos a
cabo y no fundamentar la decisión en la inercia y la
tradición ("aquí las cosa siempre se han hecho
así").

Muestreo por atributos: simple, doble y
múltiple

El plan de muestreo simple consiste en un
tamaño de muestra n, y en un número de
aceptación c, ambos fijados de antemano. Si en la
muestra se encuentra c o menos unidades defectuosas
entonces el lote es aceptado. Por el contrario, si hay más
de c artículos defectuosos el lote es rechazado.
Mas adelante veremos cómo diseñar este tipo de
planes.

Por su parte, la idea del plan de muestreo doble es
tomar una primera muestra de tamaño más
pequeño que el plan simple para detectar los lotes muy
buenos o los muy malos, y si en la primera muestra no se puede
decidir si aceptar o rechazar porque la cantidad de unidades
defectuosas ni es muy pequeña ni muy grande, entonces se
toma una segunda muestra para decidir si aceptar o rechazar
tomando en cuenta las unidades defectuosas encontradas en las dos
muestras. De esta manera, un plan de muestreo doble está
definido por

N = tamaño de lote

n1 = tamaño de la primera
muestra

c1 = número de aceptación para
la primera muestra

n2 = tamaño de la segunda
muestra

c2 = número de aceptación para
las dos muestra

Por ejemplo, con el plan N = 3000,
n1 = 80, c1 = 1,
n2 = 80, c2 = 4; del lote de
3000 piezas se toma una muestra inicial de 80 y con base a la
información aportada por esta primera muestra se toma una
de las tres decisiones siguientes:

1. Aceptar el lote, cuando la cantidad de unidades
   defectuosas sea menor o igual que 1
   (c1).
2. Rechazar el lote, cuando el número de piezas
   defectuosas sea mayor que 4 (c2).
3. Tomar una segunda muestra de 80 unidades, cuando el
   número de piezas defectuosas detectadas en la primera
   muestra sea mayor que 1 (c1) pero no exceda
   de 4 (c2). Si al sumar la cantidad de
   unidades defectuosas en las dos muestras, esta no es mayor que
   4 (c2), el lote es aceptado, pero si es mayor
   que 4 (c2), entonces el lote es
   rechazado

El plan de muestreo múltiple es una
extensión del concepto del muestreo doble, aquí se
toma una muestra inicial aún más pequeña que
el plan simple, y si ya se tiene evidencia de muy buena o muy
mala calidad se toma la decisión en consecuencia, si no,
se toma una segunda muestra y se trata de decidir; si
todavía no es posible se continúa con el proceso
hasta tomar la decisión de aceptar o rechazar.

Con los planes de muestreo doble y múltiple por
lo general se requieren menos inspección que con el
simple, pero tienen mayor dificultad para administrarlos. En
cuanto a seguridad pueden ser diseñados de forma que
produzcan resultados equivalentes.

Esto es, los procedimientos
pueden ser diseñados de manera que un lote con cierta
calidad específica tenga exactamente la misma probabilidad
de aceptación bajo los tres tipos de planes de muestreo.
Por consiguiente, para la selección
de un tipo de muestreo, se pueden considerar factores como la
eficacia de
la
administración, el tipo de información obtenida
por el plan, la cantidad promedio de información y el
impacto que un plan de muestreo dado pueda tener sobre el flujo
del proceso.

FORMACIÓN DEL LOTE Y SELECCIÓN DE LA
MUESTRA

La formación de un lote puede influir en la
eficacia del plan de muestreo de aceptación. A
continuación se enuncia tres recomendaciones para formar
los lotes, aunque una de ellas se debe ver como
reserva.

2. Los lotes deben ser homogéneos. Es
   decir, las unidades que forman un lote en particular deben
   haber sido fabricadas bajo condiciones similares en cuanto a
   máquinas, operadores, materia
   prima, tiempo (fechas), etcétera. Cuando el lote se
   forma mezclando unidades de diferentes fuentes, el
   muestreo de aceptación no es tan efectivo como se debe.
   Además la existencia de lotes no homogéneos hace
   más difícil tomar acciones
   correctivas que eliminan la causa de los productos defectuosos.
   De esa manera, cuando se forme un pedido o embarque es mejor
   inspeccionar cada lote individual y evitar aplicar la
   inspección a todo el pedido después de que se han
   mezclado lotes.
3. Los lotes deben ser formados de manera que no
   compliquen el manejo de materiales
   del proveedor y del cliente. Todos los artículos de
   los lotes deben ser empaquetados y embarcados con un
   mínimo de riesgo y de forma que la selección de
   unidades de la muestra sea relativamente
   fácil.
4. Con las reservas del caso, otra recomendación
   tradicional es: los lotes deben ser tan grandes como sea
   posible. Esto debido al menor costo y mayor eficiencia de
   la inspección, ya que en los lotes grandes es necesario
   inspeccionar menos proporcionalmente que con los lotes
   pequeños, y además los planes resultantes a
   partir de tamaños de lote grande tienen mayor poder de
   detectar los lotes de mala calidad.

Creemos que en empresas con sistema de
mejora de calidad esta recomendación se debe ver con
mucha reserva, ya que esto que es deseable para el muestreo de
aceptación no es recomendable para los inventarios en
procesos y en producto terminado. Con lotes muy grandes se
aumenta el costo de inventarios, el tiempo de ciclo y disminuye
la capacidad de detectar con oportunidad las anomalías
en calidad. De aquí que tal recomendación se debe
aplicar en la medida que no se afecte sensiblemente los
aspectos comentados.

Selección de la muestra

Todos los planes de muestreo de aceptación basan
su funcionamiento en que las unidades seleccionadas para la
inspección son representativas de todo el lote. De
aquí que la selección de las unidades que forman la
muestra debe hacerse aplicando un método de
muestreo aleatorio. La técnica de muestreo es muy
importante y la que a menudo se sugiere es el muestreo
aleatorio simple, en la que se asigna un número a cada
artículo del lote. Entonces, entre 1 y el número
máximo de unidades en el lote se seleccionan
aleatoriamente n números. Esta sucesión de
números aleatorios determina cuáles
artículos del lote constituyen la muestra.

Si los productos están seriados o tienen un
código
de números, éstos pueden ser utilizados para
desarrollar el muestreo aleatorio. Otra opción es usar un
número aleatorio de tres dígitos. Por ejemplo el
número 482 puede ser la representación de la unidad
localizada sobre un cuarto nivel, octava fila y segunda
columna.

En circunstancias donde no se puede asignar un
número a cada unidad, es posible emplear alguno de los
otros métodos de
muestreo que aseguren que el muestreo es aleatorio o
representativo. Por ejemplo el inspector podría
estratificar el lote, dividiéndolo en estratos o capas y
cada estrato en cubos, como se muestra en la figura 2. Las
unidades son tomadas dentro de cada cubo. Entre más formal
sea esta división o estratificación, mayor
representatividad tendrá la muestra.

Si por alguna razón esta división no es
posible, entonces dentro de los males, el menor es que la
estratificación se realice de manera imaginaria por el
inspector, con lo que no necesariamente se obtendrá
muestras aleatorias, pero al menos se tiene la seguridad de que
las unidades son tomadas desde diferentes zonas del
lote.

Si se utilizan métodos arbitrarios para
seleccionar una muestra, las bases teóricas del muestreo
de aceptación no se cumplen y por tanto las decisiones
sobre el lote no tendrán un respaldo
estadístico.

Figura 2. División de un
lote por muestreo

ASPECTOS ESTADÍSTICOS: VARIABILIDAD Y CURVA
CARACTERÍSTICA DE OPERACIÓN

Suponga que se tiene gran cantidad de productos y se
sabe que el índice de producto defectuoso es el 6%. Si
tomamos una muestra de tamaño de 100 con muy buena
representatividad, entonces por lógica
se esperaría que en cada muestro encontremos 6 productos
defectivos. Sin embargo, la misma experiencia ha demostrado que
se puede encontrar más o menos 6 defectivos, la
razón es que los artículos extraídos en cada
muestra depende del azar, por lo que la cantidad de
artículos defectuoso es variable y es "difícil" que
en las muestras vengan exactamente 6 defectuosos.

Siempre que el azar está de por medio, los
resultados son variables y el objetivo de la
probabilidad y la estadística es modelar (predecir) tal
variabilidad, para que así el "azar" no sea capricho.
Así en el caso particular que hemos planteado,
quizá sea razonable pensar que la mayoría de las
veces que repitamos el proceso de extraer una muestra de 100
artículos, la cantidad de piezas defectivas encontradas
varíe alrededor de 6. Pero la pregunta es
¿qué tan cercano a 6? La respuesta la da la
distribución de probabilidad binomial, que
es la distribución que modela las más de las veces
este tipo de situaciones que hemos planteado antes. Se puede
encontrar la probabilidad de obtener cierta cantidad, x,
de productos defectuosos en cada muestra de tamaño de 100,
sabiendo que la población o lote de donde se extrae la
muestra de manera aleatoria tiene cierto porcentaje de productos
defectuosos aleatoriamente mezclados en el lote. A
continuación se muestran estas probabilidades.

Aplicación de la
distribución binomial (100, 0.06)

Existen muchos sistemas
computacionales para calcular lo anterior. Por ejemplo, en
Excel las
probabilidades de la tabla anterior se calculan con la
función DISTR.BINOM (x, n, p, 0). Donde x es
la cantidad de defectuosos, n es el tamaño de
muestra (n = 100, en el ejemplo), p es la
proporción artículos defectuosos en el lote o
población (p = 0.06 en el ejemplo), y 0 es un valor
lógico.

De esta manera, a partir de la tabla se observa que si
en la situación descrita se siguen extrayendo muestras de
tamaño de 100 y en la producción se mantiene 6% de
artículos defectuosos, entonces se espera que solo en
16.6% de las muestras se observen exactamente 6 artículos
defectuosos. Lo anterior debe tomarse en cuenta siempre que se
haga inspección por muestras: lo que se observa de una
muestra no es idéntico lo que hay en la población o
lote, ya que lo que se observa de una muestra a otra tiene cierta
variabilidad. Por tanto, para tomar cualquier decisión
sobre la población, lo primero que se debe hacer es
conocer tal variabilidad. Así, forzosamente se tiene que
aplicar algún modelo
probabilístico. En muestreo de aceptación tal
modelo probabilístico es la curva característica de
operación.

Curva característica de operación
(CO)

Suponga que en una fábrica se aplica a lotes de
tamaño grande (es usual considerar que un lote es grande
respecto al tamaño de la muestra, cuando la muestra es
menos del 10% del lote, es decir, cuando 10n <
N) el plan de muestreo simple por atributos definido
por

n = 60, c =1

a los lotes de ciertos artículos antes de
embarcarlos y enviarlos al cliente. De esta manera, de un lote de
más de 600 piezas, se extrae una muestra aleatoria de
n = 60, y si al inspeccionar estas unidades se encuentran
cero o a lo más una defectuosa, entonces el lote es
aceptado (embarcado y enviado al cliente). Pero si se encuentran
dos artículos o más que son defectuosos, entonces
el lote es rechazado (retenido para una inspección al
100%).

Bajo estas condiciones surgen algunas interrogantes: que
tipo de calidad garantiza este plan y cuál es el nivel de
calidad que no tolera; o de una manera más técnica:
si un lote tiene cierta proporción de artículos
defectuosos, ¿cuál es la probabilidad de que el
lote sea aceptado? Las respuestas a estas preguntas se obtiene a
partir de la curva característica de operación
(curva CO) para el citado plan.

La curva CO de un plan proporciona una
caracterización del potencial desempeño del mismo, ya que con ésta
se puede saber la probabilidad de aceptar o rechazar un lote que
tiene determinada calidad. Por ejemplo, con la curva CO del plan
n = 60, c =1 y tamaño de lote grande, se
puede saber cual es la probabilidad de aceptar un lote que tenga
2% de sus artículos defectuosos. Además, como de un
lote que se somete a inspección por muestreo se desconoce
su proporción, p, de artículos defectuosos,
entonces la curva CO tiene que proporcionar la probabilidad de
aceptar lotes con cualquier valor de p. En la figura 3 se
muestra la curva CO para el plan n = 60, c
=1.

Figura 3 Curva CO para el plan
de muestreo n = 60, c = 1 y tamaño de lote
grande

Obtener los puntos sobre la curva CO es relativamente
fácil. Supóngase que el lote proviene de un flujo
continuo de productos que puede ser considerado infinito o que el
lote tiene un tamaño N que es grande respecto al
tamaño de muestra. Bajo esta condición, la
distribución del número de artículos
defectuosos, x, en la muestra aleatoria de tamaño
n, es binomial con parámetros n y p;
donde p es la proporción de artículos
defectuosos en el lote. La probabilidad de observar exactamente
x defectuosos en la muestra esta dada por la
ecuación:

símbolo factorial (5! = 5 x 4 x 3 x 2 x 1 = 120,
por ejemplo). A p se le desconoce la mayoría de las
veces.

De esta manera la probabilidad de aceptación es
justamente la probabilidad que x sea menor o igual que
c. Por ejemplo, la probabilidad de aceptar un lote que
tenga 2% de artículos defectuosos (p = 0.02) con el
plan n = 60, c = 1, es igual a la probabilidad de
que x sea menor o igual a 1; es decir, es igual a la
probabilidad de obtener cero artículos defectuosos
más la probabilidad de obtener uno.

P(0) + P(1).

Al calcular estas probabilidades con la
distribución binomial con n = 60 y p = 0, se
obtiene.

P(0) = 0.2976

P(1) = 0.3633

Por lo que la probabilidad de aceptar un lote que tenga
2% de artículos defectuosos con este plan es igual a
0.6619. Probabilidad que se podría haber apreciado
más o menos directamente de la curva CO de la figura 3, ya
que esta curva se obtiene calculando P(0) + P(1) con la formula
de distribución

binomial, con n = 60, para diferentes valores de
p. En la tabla 1 se aprecia la probabilidad de
aceptación de lotes con diferentes valores de p; y
con base en la tabla 1 se puede bosquejar la curva CO de la
figura 3

Tabla 1 Probabilidad de aceptación del
plan n = 60, c =1, para

Diferentes valores de p y suponiendo
tamaño de lote grande.

Así, la curva CO de la figura 3 muestra el poder
de discriminación del plan de muestreo
n = 60, c =1. Por ejemplo, si los lotes tienen 5%
de artículos defectuosos (p = 0.05), entonces la
probabilidad de aceptarlos es aproximadamente 0.19. Esto
significa que si 100 lotes con 5% de defectuosos, son sometidos a
este plan de muestreo, entonces se esperaría aceptar a 19
y rechazar a 81.

En general, para obtener una curva CO para un plan con
tamaño de muestra n y número de
aceptación c, se calcula la probabilidad de
aceptación, Pa, para diferentes valores de la
proporción de defectuosos, p; es decir, se
calcula.

Pa = P(0) + P(1)+ ….. +P(c); para
diferentes valores de p.

Curva CO ideal

Si se quieren rechazar los lotes que tengan una
proporción de artículos defectuosos mayor que 1%
por ejemplo, y aceptar los que tengan 1% de defectuosos o menos.
La curva CO ideal para esta situación se muestra en
la figura 4, en la que si el nivel de calidad es 1% de defectivo
o menos, se está satisfecho con tal cantidad y por tanto
se acepta con probabilidad 1. Mientras que si la
proporción de defectivos es mayor que 1% no se está
satisfecho con esa calidad por lo que se desea aceptarla con
probabilidad cero (es decir, rechazarla con probabilidad 1). Sin
embargo, no existe ningún plan de muestreo que tenga esta
curva ideal y que por tanto sea capaz de hacer una discriminación perfecta entre los lotes
"buenos" y "malos". En teoría
la curva CO ideal se puede alcanzar con inspección al
100%, siempre y cuando esta inspección estuviera libre de
errores, lo que difícilmente ocurre.

Figura 4 Curva CO ideal para la
calidad p = 0.01 (1%).

De acuerdo con lo anterior, lo más que se puede
hacer en la práctica es diseñar planes de muestreo
de aceptación que tengan alta probabilidad de aceptar
lotes buenos, y una baja probabilidad de aceptar lotes malos. Por
ejemplo, con el plan n = 60, c =1 (véase
tabla 1 figura 3), se tiene una probabilidad de 0.879 de aceptar
lotes con proporción de defectuosos de 1% y para
porcentajes menores a este 1% se tiene mayor probabilidad de
aceptación; pero lotes con 4% de defectivo todavía
tienen probabilidad de aceptarse de 0.30. Por lo que si se quiere
un plan más estricto que no permita pasar tan
fácilmente lotes de ese tipo, entonces será
necesario diseñar un plan con un tamaño de mayor
muestra, como lo veremos enseguida.

Propiedades de las curvas CO

2. No existe un plan de muestreo que tenga una curva CO
   ideal, que pueda distinguir perfectamente los lotes
   buenos de los malos. De esta manera, todo plan de muestreo
   tiene riesgos de rechazar la buena calidad y aceptar la mala.
   Lo que sí existe son planes que tienen mayor
   probabilidad de aceptar la buena calidad y menos probabilidad
   de aceptar la mala.

   Plan n = 60, c = 1;
   probabilidad de aceptarlo 0.302

   Plan n =120, c = 2;
   probabilidad de aceptarlo 0.137

   Plan n =240, c = 4;
   probabilidad de aceptarlo 0.035

   De esta manera, el último plan sólo
   dejará pasar 3.5% de lotes con 4% de
   defectivo.

3. Al aumentar el tamaño de la muestra con el
   número de aceptación, se obtiene planes
   cuya curva CO se acerca más a la ideal, es decir, que
   tienen mayor potencia
   en distinguir la buena calidad de la mala. Esta propiedad
   queda en evidencia en la figura 5, en la que se muestran las
   curvas CO de tres planes de muestreo, nótese que entre
   mayor es n más rápido cae la curva, no
   obstante que el número de aceptación c
   se mantiene proporcional al tamaño de muestra. Entre
   más rápido caiga la curva, menos probabilidad
   se tiene de aceptar lotes de mala calidad. Por ejemplo,
   suponga que un lote con 4% de defectivo se considera como de
   mala calidad, entonces con las tres curvas de la figura 5 se
   tiene que:

   N = 300 n = 30 c
   = 0

   N = 500 n = 50 c
   = 0

   N = 800 n = 80 c
   = 0

   En la figura 6 se muestran las curvas CO para estos
   tres planes. De donde se puede ver que estos tres planes,
   obtenido con el mismo criterio (no estadísticos),
   proporcionan distintos niveles de protección para un
   mismo nivel de calidad en los lotes. Por ejemplo, si los
   lotes tienen una proporción de defectivo de 0.05 (5%),
   entonces la probabilidad de aceptarlo, Pa, en cada
   caso es el siguiente:

   N = 300, Pa = 0.214;
   N = 500, Pa = 0.0769; N = 800, Pa
   = 0.0165;

   Así, en el primer caso se aceptará
   21.4% de los lotes, en el segundo 7.69% y en el último
   1.65%. Por lo anterior, obtener el tamaño de muestra
   con tal criterio de porcentaje es inadecuado.

   

   Figura 5 Cuando n crece
   y c lo hace de manera proporcional, aumenta el poder
   de discriminación de un plan.

   

   Figura 6 Curvas CO para
   tamaño de muestra igual al 10% del lote y c =
   0.

4. El criterio de tamaño de muestra
   igual a un porcentaje del tamaño de lote es un mal
   criterio. Es frecuente encontrar casos en los que el
   tamaño de la muestra se tome igual a cierto porcentaje
   del tamaño del lote y el número de
   aceptación c = 0. Si este porcentaje es 10%, por
   ejemplo, y se tiene lotes de tamaño N, igual a
   300, 500 y 800, entonces al aplicar este criterio se obtiene
   que los planes de muestreo de aceptación para estos
   lotes son:
5. Al disminuir el número de aceptación
   la curva CO cae más rápido y con ello los
   planes se vuelven más estrictos. Esto se puede
   apreciar en las curvas CO para los planes n = 80
   c = 0, n = 80 c = 1, n = 80
   c = 2, que se muestra en la figura 7.

   

   Figura 7 El efecto de
   disminuir c en los planes de muestreo por
   atributos.

6. Los planes con c = 0 no siempre son lo más
   apropiados. En la figura 6 también se pueden
   apreciar curvas CO para varios planes con número de
   aceptación c = 0, y si la comparamos con las
   curvas CO de la figura 5, vemos que las de c = 0 son
   cóncavas hacia arriba; lo que causa que la probabilidad
   de aceptar disminuya más rápido aun para valores
   pequeños de la proporción de defectivo en el
   lote. Esto hace que sean planes extremadamente exigentes para
   el proveedor y en algunas circunstancias costosos para el
   cliente. Por ejemplo, si el nivel aceptable de calidad es 1%
   quiere decir que se aceptan con gusto los lotes que tengan una
   proporción de defectivo de 1% o menos; bajo estas
   condiciones si optamos por aplicar el plan n = 120
   c = 2 (figura 5), entonces la probabilidad de aceptar
   lotes con 1% de defectivo es 0.88. Pero si se aplica el plan
   n = 30 c = 0, la probabilidad de aceptarlos es
   menor (Pa = 0.74); lo que llevaría a rechazar 26%
   de los lotes que tengan un nivel de calidad aceptable. De esta
   manera, diseñar planes con c = 0, que
   intuitivamente se pensaría que funcionan mejor, no
   siempre es recomendable.
7. La influencia del tamaño de lote es
   diseñar planes adecuados de muestreo, es menor de lo que
   continuamente se cree. Curvas CO tipo A y tipo B. Para
   obtener todas las curvas CO que hemos visto hasta aquí,
   se ha supuesto que las muestra se extraen de un lote grande o
   que el lote proviene de un flujo continuo de productos. A este
   tipo de curvas se les conocen como curvas CO tipo B, y
   la distribución apropiada para calcular las
   probabilidades de aceptación es binomial.

La curva CO de tipo A se utiliza en el cálculo
de las probabilidades de aceptación par un lote aislado
y de tamaño finito. En este caso, si el tamaño
del lote es N, el de la muestra es n y el
número de aceptación es c, entonces la
distribución exacta del número de
artículos defectuosos en la muestra es la
distribución hipergeométrica.

En la figura 8 se muestran las curvas CO exactas tipo
A para los planes de muestreo simple: tamaño de lote
N = 200, n = 80 c = 1; N = 800,
n = 80 c = 1; y la curva tipo B para
tamaño de lote muy grande (infinito), N = Inf.,
n = 80 c = 1. De ahí se puede ver que la
discrepancia entre las tres curvas es relativamente poca, por
ejemplo para p = 0.04, se tienen las siguientes
probabilidades de aceptación Pa = 0.1016, 0.1508
y 0.1653, respectivamente.

Figura 8 Curvas CO para el plan
n = 80 y c = 1, pero con tamaño de lote
diferente.

En particular, si el tamaño de lote es 10 veces
mayor que el tamaño de muestra, la diferencia entre las
curvas tipo A y tipo B es considerablemente pequeña. De
aquí que en estos casos el tamaño de lote influye
poco en la probabilidad de aceptar el lote.

Cuando el tamaño de lote no es 10 veces mayor que
el tamaño de la muestra como en el caso del plan N
= 200, n = 80, c = 1, entonces la probabilidad de
aceptar el lote se ve más afectada por el tamaño
del lote, pero generalmente es menor de lo que la
intuición de las personas supone, como se puede ver en la
figura 12.8.

ÍNDICES DE CALIDAD PARA LOS PLANES DE
MUESTREO DE ACEPTACIÓN

En una relación cliente-proveedor en la que hay
un plan de muestreo de aceptación de por medio, hay dos
intereses: por un lado, el proveedor quiere que todos los lotes
que cumplen con un nivel de calidad aceptable sean aceptados, y
por el otro, el cliente desea que todos los lotes que no tienen
un nivel de calidad aceptable sean rechazados.

Desafortunadamente ambos intereses no pueden ser
satisfechos de manera simultanea por un plan de muestreo de
aceptación y explicamos la razón de ello cuando
vimos la curva CO ideal. Ante esta situación lo que se
hace para atender parcialmente ambos intereses es diseñar
planes de muestreo de aceptación que tenga alta
probabilidad de aceptar lotes buenos, y una baja probabilidad de
aceptar lotes malos. El punto de partida para diseñar
planes de muestreo que logren lo anterior es definir
índices de calidad para los planes de muestreo que
establezcan en una relación cliente-proveedor
específica, lo que se considerará como calidad
aceptable, intermedia y no aceptable con sus correspondientes
probabilidades de aceptación.

En este sentido, los principales índices de
calidad con los que se diseñan y caracterizan los planes
de muestreo, son los siguientes.

Nivel de calidad aceptable, NCA o AQL
(aceptancing quality level). El NCA se define como
el porcentaje máximo de unidades que no cumplen con la
calidad especificada, que para propósitos de
inspección por muestreo se puede considerar como
satisfactorio o aceptable como un promedio para el proceso. El
NCA también se lo conoce como nivel de calidad del
productor y se expresa en porcentajes de unidades que no
cumplen con la calidad especificada. Al ser el NCA el nivel de
calidad que se considera satisfactorio, entonces la probabilidad
de aceptar un lote que tenga esa calidad debe ser alta (0.95)
(ver figura 9). A la probabilidad de aceptar lotes
que tengan un nivel da calidad aceptable (NCA), se lo designa con
1 – α, donde α es por lo general un
nϊmero pequeño (0.05, 0.10).
Nótese que la probabilidad de aceptar lotes de calidad
aceptable no es igual a 1 y por tanto hay un riesgo
de no aceptar este tipo de lotes. A este riesgo que tiene
probabilidad igual a α se le conoce como
riesgo del productor.

Debido a este riesgo, el NCA debe ser un nivel de
calidad de referencia para el proceso de producción del
productor y de ninguna manera un valor objetivo.

Más aún, el productor debe trabajar para
que su procese opere con un nivel mejor que el NCA.

Nivel de calidad límite, NCL o LQL
(limiting quality level). Es el nivel de calidad que se
considera como no satisfactorio y que los lotes que tengan este
tipo de calidad deben ser rechazados casi siempre. El NCL, en
algunos planes específicos (por ejemplo los "Planes de
muestreo Dodge-Roming") se conoce como porcentaje defectivo
tolerado del lote, PDTL o LTPD (lot tolerance percent
defective). Al ser el NCL un nivel de calidad no
satisfactorio, entonces la probabilidad de aceptarlo debe ser muy
baja (generalmente de 0.05, 0.10); es usual que esta probabilidad
se le designe con la letra β (vιase figura
9). Nótese que la probabilidad de aceptar
lotes de calidad no satisfactorio (NCL) no es cero y por tanto
hay un riesgo de no rechazar este tipo de lotes. A este riesgo
que tiene probabilidad igual a β se lo conoce como
riesgo del consumidor.

EJEMPLO 1

Suponga que un cliente plantea la necesidad de que su
proveedor le envié sólo aquellos lotes que tengan
un buen nivel da calidad. Para ello se decide establecer un plan
simple de muestreo de aceptación. El tamaño de lote
es grande y se establece con el porcentaje de unidades
defectuosas que se considera aceptable o satisfactorio es del
0.4%, NCA = 0.4%, y se acuerda que este tipo de calidad adecuada
tendrá probabilidad de aceptarse del 0.95, y por tanto un
riesgo de no aceptarse de 0.05. El riesgo del
productor es α = 0.05, ya que los lotes del productor que
tengan 0.4% de defectuosos, a pesar de tener una calidad
aceptable, tienen probabilidad de no aceptarse de
0.05.

También se acuerda que el nivel de calidad que se
considerará como no aceptable o insatisfactorio es de
2.55%, NCL = 2.55%. Por ello los lotes que tengan este porcentaje
de unidades defectuosas tendrán baja probabilidad de
aceptarse (0.10); de esta manera el cliente (consumidor)
está asumiendo un riesgo de β = 0.10 de aceptar lotes
de calidad pobre (2.55% de defectuosos).

Bajo las condiciones anteriores, un plan de muestreo que
cumple moderadamente bien los acuerdos del cliente y el proveedor
es n = 205 c = 2, cuya curva CO se muestra en la
figura 9. Es importante entender bien el funcionamiento de este
plan: garantiza que los lotes que tengan un porcentaje de
unidades defectuosas menor o igual a 0.4% se aceptarán con
facilidad. A medida que este porcentaje vaya siendo mayor, cada
vez será más difícil (menos probable) que
los lotes correspondientes sean aceptados. En particular si un
lote tiene un porcentaje del 2.55%, entonces tendrá
probabilidad de ser aceptado de 0.10.

En consecuencia, este plan no garantiza que los lotes
con un porcentaje de defectuosos mayor a 0.4% sean rechazados
siempre.

Figura 9 Curva CO
con NCA = 0.4%, α = 0.05, NCL =
2.55% y β = 0.10

Calidad promedio de salida, CPS o
AOQ (average outgoing quality). Es la calidad promedio que
se alcanza después de aplicar el proceso de
inspección. Este concepto es otra forma de medir el efecto
de un plan de muestreo sobre la calidad que se tendrá
después de aplicar el plan.

Cuando un programa de
muestreo de aceptación aplica muestreo 100% a los lotes
rechazados, entonces la calidad de salida de esos lotes es
perfecta (si no hay error de inspección), ya que todas las
unidades defectuosas de esos lotes son sustituidas por
artículos buenos. Mientras que en los lotes que son
aceptados, su calidad de salida después de la
inspección puede ser que mejore un poco, porque las
unidades defectuosas encontradas n las muestras son reemplazadas
por unidades buenas.

De esta manera, independientemente si el lote sea
aceptado o rechazado, la calidad que llega al cliente tiende a
ser mejor que la que tenían los lotes antes de ser
inspeccionado.

Por lo anterior, una forma de caracterizar la bondad de
un plan de muestreo de aceptación es calcular la calidad
promedio de salida que genera. Este cálculo se hace de
forma similar a como se obtiene la curva característica de
operación, ya que para cada proporción de
defectuosos que contiene el lote en la entrada se espera una
proporción promedio de defectuosos de salida (CPS). Al
graficar la proporción de entrada, p, contra la
proporción promedio de defectuoso después de la
inspección, CPS, se obtiene una curva para la calidad
promedio de salida (curva CPS). En la figura 10 se muestra
tal curva para el plan n = 60, c = 1.

Figura 10 Curva para la
capacidad promedio de salida, CPS, del plan n = 60, c
= 1.

La obtención de la curva CPS, cuando se tiene
tamaño de lote grande, se hace calculando la
proporción promedio de defectuosos de salida, CPS, con la
siguiente fórmula:

CPS = p * Pa

Donde p es la proporción de defectuosos a
la entrada del lote, y Pa la probabilidad de
aceptación de tal lote que proporciona el plan de
muestreo. De esta manera, si ya se tienen los cálculos
para la curva CO, como en la tabla 1, entonces al multiplicar la
columna p por la Pa se obtiene CPS para cada valor
de p, como se aprecia en la tabla 2. A partir de esta
tabla se puede ver que si los lotes entran con una
proporción de defectuosos, de 0.04 (4%) por ejemplo, y se
someten a inspección muchos lotes con esta calidad
inicial, una parte será aceptada (aproximadamente 30.2%) y
la otra rechazada (y por tanto inspeccionada al 100%); entonces
después de aplicar el plan de muestreo una parte de esos
lotes tendrán la proporción de defectuosos de cero
y la otra parte su proporción será poco menor o
igual a 0.04, y al promediar estas proporciones obtendremos un
promedio de 0.01208 (1.2%).

Limite de la calidad promedio de salida, LCPS o
AOQL (average outgoing quality limit). Es el valor
máximo de la curva CPS que vimos antes, y representa el
peor promedio de calidad que puede obtenerse del programa de
inspección. Por ejemplo, para el plan n = 60,
c = 1, y examinando la figura 10 y la tabla 2, se puede
ver que el LCPS es aproximadamente 0.014; esto es, no importa que
tan mala sea la proporción de defectuosos en los lotes que
entran, la calidad promedio de salida nunca será peor que
1.4% de defectuosos en promedio. Desde luego que esto no
significa que el plan no acepte lotes con calidad peor a 1.4%,
más bien se está hablando de un límite
promedio que es valido después de aplicar el plan de
referencia a muchos lotes de un flujo continuo de
producción.

Algunos planes de muestreo obtienen el tamaño de
muestra a partir del LCPS deseado. Por ejemplo los de
Dodge-Roming.

Inspección total promedio, ITP o ATI
(average total inspection). Otro aspecto importante para
evaluar un plan de muestreo de inspección es la cantidad
total de inspección que requiere. Una vez aceptados los
lotes, la cantidad de inspección es una muestra de
tamaño n. Por el contrario, los lotes que son
rechazados son sometidos al 100% de inspección y la
cantidad de inspección por lote será de
tamaño N. De esta manera, la cantidad promedio de
inspección por lote varia entre el tamaño de
muestra n y el tamaño de lote N. Si el lote
es de calidad p y la probabilidad de aceptación del
lote es Pa, entonces la inspección total promedio
por lote es:

ITP = n + (1 – Pa)(N –
n)

Por ejemplo, si se tiene un tamaño de lote de
N = 5000, y se aplica el plan n = 60, c = 1,
entonces para los lotes con una proporción de defectuosos
de 0.04, se tiene que la Pa = 0.3022(tabla 2), y por
tanto

ITP = 60 + (1 – 0.3022)(5000
– 60) = 3507.13

Tabla 2. Calidad promedio de
salida, CPS, plan n = 60, c = 1.

Que es un número promedio de unidades
inspeccionadas sobre muchos lotes que tienen una
proporción de defectuosos de p = 0.04. Para cada
proporción de defectuosos p, en el lote de entrada
se puede calcular ITP, y de esa forma al aplicar la
fórmula anterior se puede trazar una curva para la ITP,
bastaría para ello saber el tamaño de lote y
agregar la columna ITP en la tabla 2.

Tabla 3. Inspección total
promedio, ITP, plan N = 5000, n = 60, c =
1.

Figura 11 Curva para la
inspección total promedio, ITP, del plan N = 5000, n
= 60, c = 1.

Xavier Armando Pillco Suárez

Estudiante de Ingenieria Industrial de Quinto
Nivel

Guayaquil – Ecuador