Medidas de dispersión (página 2)

El rango de la distribución de frecuencias se calcula
así:

R= (lim. Sup. de la clase n
– lim. Inf. De la clase 1)

= (93.910 – 7.420) =
86.49

• Propiedades del Rango o
  Recorrido:

• El recorrido es la medida de dispersión
  más sencilla de calcular e interpretar puesto que
  simplemente es la distancia entre los valores
  extremos (máximo y mínimo) en una
  distribución
• Puesto que el recorrido se basa en los
  valores extremos éste tiende s ser
  errático. No es extraño que en una
  distribución de datos
  económicos o comerciales incluya a unos pocos valores
  en extremo pequeños o grandes. Cuando tal cosa sucede,
  entonces el recorrido solamente mide la dispersión con
  respecto a esos valores anormales, ignorando a los
  demás valores de la variable.
• La principal desventaja del recorrido es que
  sólo esta influenciado por los valores extremos,,
  puesto que no cuenta con los demás valores de la
  variable. Por tal razón, siempre existe el peligro de
  que el recorrido ofrezca una descripción distorsionada de la
  dispersión.
• En el control de
  la calidad se
  hace un uso extenso del recorrido cuando la
  distribución a utilizarse no la distorsionan y cuando
  el ahorro del
  tiempo al
  hacer los cálculos es un factor de
  importancia.

1.2.-
LA VARIANZA (S2 ó δ2
):

La varianza es una medida de dispersión relativa
a algún punto de referencia. Ese punto de referencia es la
media aritmética de la distribución. Más
específicamente, la varianza es una medida de que tan
cerca, o que tan lejos están los diferentes valores de su
propia media aritmética. Cuando más lejos
están las Xi de su propia media
aritmética, mayor es la varianza; cuando más cerca
estén las Xi a su media menos es la varianza. Y
se define y expresa matemáticamente de la siguiente
manera:

La varianza para datos no
agrupados

Dado un conjunto de observaciones, tales como
X1, X2, … , Xn, la
varianza denotada usualmente por la letra minúscula
griega δ (sigma) elevada al cuadrado
(δ2)y
en otros casos S2 según otros
analistas, se define como: el cuadrado
medio de las desviaciones con respecto a su media
aritmética"

Matemáticamente, se expresa como:

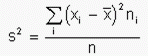
Ejemplo:

Se tienen las edades de cinco estudiantes
universitarios de Ier año, a saber: 18,23, 25, 27, y
34. Al calcular la media aritmética (promedio de las
edades, se obtuvo 25.4 años, encontrar la varianza de
las edades de estos estudiantes:

Para calcular se utiliza una tabla estadística de trabajo de
la siguiente manera:

Respuesta: la varianza de las edades es de 27.4
años

La varianza para datos
agrupados

Si en una tabla de distribución de frecuencias.
Los puntos medios de
las clases son X1, X2, … ,
Xn; y las frecuencias de las clases f1,
f2, … , fn; la varianza se calcula
así:

Σ(Xi-)2f1

δ2
= —————-

Σfi

Sin embargo la formula anterior tiene
algún inconveniente para su uso en la practica, sobre
todo cuando se trabaja con números decimales o cuando la
media aritmética es un número entero. Asimismo
cuando se trabaja con máquinas
calculadoras, La tarea de computar la varianza se simplifica
utilizando la formula de computación que se da a
continuación:

ΣXi2fi
–
[(ΣXifi)2/N]

δ2 =
—————————-

N donde
N=Σfi

Ejemplo:

Se tienen los datos de una muestra de 30
cuentas por
cobrar de la tienda Cabrera’s y
Asociados dispuestos en una tabla de
distribución de frecuencias, a partir de los cuales se
deberá calcular la varianza, para lo cual se construye
la siguiente tabla estadística de trabajo, si se
calculó anteriormente la media aritmética y se
fijó en 43.458 (ver ejemplo del calculo en "media
aritmética para datos agrupados) de la siguiente
manera

= 21,649.344 / 30 = 721.645

Respuesta: la varianza de las cuentas por
cobrar es igual B/.721.645

• Propiedades de la varianza :

• s siempre un valor no
  negativo, que puede ser igual o distinta de 0. Será 0
  solamente cuando Xi=
• La varianza es la medida de dispersión
  cuadrática optima por ser la menor de
  todas.
• Si a todos los valores de la variable se le suma
  una constante la varianza no se modifica.
  Veámoslo:

Si a xi le sumamos una constante xi’ = xi + k
tendremos (sabiendo que )

• Si todos los valores de la variable se multiplican
  por una constante la varianza queda multiplicada por el
  cuadrado de dicha constante. Veámoslo:

Si a xi’ = xi · k tendremos (sabiendo que
)

• Si en una distribución obtenemos una serie
  de subconjuntos disjuntos, la varianza de la
  distribución inicial se relaciona con la varianza de
  cada uno de los subconjuntos mediante la
  expresión

Siendo

Ni è el nº
de elementos del subconjunto (i)

S2i è la
varianza del subconjunto (i)

1.3.- LA DESVIACIÓN ESTÁNDAR (S
ó δ)

Es una medida de la cantidad típica en la
que los valores del conjunto de datos difieren de la
media. Es la medida de dispersión más
utilizada, se le llama también desviación
típica. La desviación estándar siempre se
calcula con respecto a la media y es un mínimo cuando se
estima con respecto a este valor.

Se calcula de forma sencilla, si se conoce la varianza,
por cuanto que es la raíz cuadrada positiva de esta. A la
desviación se le representa por la letra minúscula
griega "sigma" ( δ ) ó por
la letra S mayúscula, según otros
analistas.

Cálculo de la
Desviación Estándar

δ =
√δ2 ó S =
√S2

Ejemplo:

Del calculo de la varianza de las
edades de cinco estudiantes universitarios de primer año
se obtuvo δ2=27.44, como la desviación
estándar es la raíz cuadrada positiva, entonces
δ = √27.44 = 5.29 años.

Igual procedimiento
se aplica para encontrar le desviación estándar
de las cuentas por cobrar de la Tienda Cabrera’s y
Asociados, recordemos que la varianza obtenida fue de 721.645,
luego entonces la desviación estándar es igual a
δ =√721.645 = 26.86 balboas.

• Propiedades de la Desviación
  Estándar

A su vez la desviación estándar,
también tiene una serie de propiedades que se deducen
fácilmente de las de la varianza (ya que la
desviación típica es la raíz cuadrada
positiva de la varianza):

• La desviación estándar es siempre un
  valor no negativo S será siempre ³ 0 por definición. Cuando S = 0
  è X = xi (para todo
  i).
• Es la medida de dispersión óptima por
  ser la más pequeña.
• La desviación estándar toma en cuenta
  las desviaciones de todos los valores de la
  variable
• Si a todos los valores de la variable se le suma
  una misma constante la desviación estándar no
  varía.
• Si a todos los valores de la variable se
  multiplican por una misma constante, la desviación
  estándar queda multiplicada por el valor absoluto de
  dicha constante.

1.4.- El Coeficiente de Variación de Pearson
(C.V.)

Las medidas de tendencia central tienen como objetivo el
sintetizar los datos en un valor representativo, las medidas de
dispersión nos dicen hasta que punto estas medidas de
tendencia central son representativas como síntesis
de la información. Las medidas de
dispersión cuantifican la separación, la
dispersión, la variabilidad de los valores de la
distribución respecto al valor central. Distinguimos entre
medidas de dispersión absolutas, que no son comparables
entre diferentes muestras y las relativas que nos
permitirán comparar varias muestras.

El problema de las medidas de dispersión
absolutas es que normalmente son un indicador que nos da problemas a la
hora de comparar. Comparar muestras de variables que
entre sí no tienen cantidades en las mismas unidades, de
ahí que en ocasiones se recurra a medidas de
dispersión relativas.

Un problema que se plantea, tanto la varianza como la
desviación estándar, especialmente a efectos de
comparaciones entre distribuciones, es el de la dependencia
respecto a las unidades de medida de la variable. Cuando se
quiere comparar el grado de dispersión de dos
distribuciones que no vienen dadas en las mismas unidades o que
las medias no son iguales se utiliza el llamado
"Coeficiente de Variación de Pearson", del
que se demuestra que nos da un número independiente de las
unidades de medidas empleadas, por lo que entre dos
distribuciones dadas diremos que posee menor dispersión
aquella cuyo coeficiente de variación sea menor., y que
se define como la relación por cociente entre la
desviación estándar y la media aritmética; o
en otras palabras es la desviación estándar
expresada como porcentaje de la media
aritmética.

Definición del Coeficiente
de Variación

Donde: C.V. representa el
número de veces que la desviación típica
contiene a la media aritmética y por lo tanto cuanto
mayor es CV mayor es la dispersión y menor la
representatividad de la media.

• Propiedades del Coeficiente de Variación
  :

• Si a todos los valores de la variable se le suma
  una misma constante el coeficiente de variación queda
  alterado .

Ejemplo:

Suponga que Usted trabaja en una
compañía de ventas, que
ofrece como premio de incentivo al mejor vendedor del trimestre
anterior las entradas al palco empresarial en la serie final de
béisbol de las grandes ligas en los Estados Unidos
(E,E,U,A,).

De los registros de
ventas se tienen los siguientes datos de ventas, expresados en
porcentajes de cumplimiento de las metas fijadas
mensualmente:

Vendedor A 95 105 100

Vendedor B 100 90 110

El promedio trimestral de cumplimiento de las metas de
ventas de ambos vendedores es igual y equivale al 100%, pero
Ud. Sólo le puede dar el premio de incentivo a uno de
ellos. ¿Cuál usted escogería?. ¿En
base a que criterio’. Explique.

Este problema se resuelve utilizando el coeficiente de
variación, para estos efectos es necesario encontrar la
desviación estándar trimestral de las ventas de
cada uno de la siguiente manera:

Vendedor A

La desviación estándar es
δ=√(50/3) = √16.667 = 4.08, luego entonces el
coeficiente de variación es igual a:

δ 4.08

C.VA= ——— =
———– = 0.0408

 100

Vendedor B

La desviación estándar es
δ=√(200/3) = √66.667 = 8.16, luego entonces
el coeficiente de variación es igual a:

Respuesta: Dado que el vendedor A tiene menor
coeficiente de variación, A él le corresponde
recibir el premio de incentivo.

LABORATORIO

(Resolver y entregar en grupos de tres
estudiantes, equivalen a nota de un parcial)

Problema #1:Datos no agrupados

Calcule el rango, la varianza y la desviación
estándar de las observaciones que se presentan a
continuación.

63 45 39 55 69 21 50 25 33 25

Problema #2:

Un profesor hace
un examen a tres estudiantes y las puntuaciones resultantes
(Xi) son: 73, 75 y 77.

1. Hallar la media, la varianza y la desviación
   estándar de esta población de valores
2. En la clase hacia un calor
   terrible, y hubo alarma por la amenaza de incendio durante el
   examen. El profesor quisiera aumentar las puntuaciones para
   tener en cuenta estas condiciones desafortunadas de
   ambientación. Un primer aumento suma 10 puntos a cada
   puntuación. Sea Yi = Xi+10.
   Halle ,
   δ2 y
   δ.
3. Un segundo aumento incrementa cada puntuación
   en un 10%. Sea Pi =1.1(Xi). Halle
   ,
   δ2 y
   δ.
4. El último aumento es una combinación de
   los dos primeros. Est es, cada puntuación se incrementa
   en un 10% y luego se suman 10 puntos más. Sea
   Zi = 1.1(Xi)+10. Halle .
   δ2 y
   δ..

Problema #3:Datos Agrupados

La distribución de frecuencias que se presenta a
continuación muestra el tiempo que se necesita para
envolver 130 paquetes que fueron enviados por correo en
Macondo.

Calcule el rango, la varianza y la desviación
estándar de la siguiente distribución de
frecuencias de los datos:

Problema #4:Coeficiente de
Variación

Los datos a continuación describen las
distribuciones de puntuaciones en determinados grupos
ocupacionales sometidos a la prueba general de clasificaciones
del ejercito durante el último año.

Compare los resultados obtenidos para cada grupo
ocupacional utilizando el coeficiente de variación y el
rango o recorrido. Comente los resultados.

Problema #5: Coeficiente de
Variación

La tabla a continuación indica los salarios
básicos por hora (en unidades monetarias) en abril 200X
para ciertas categorías ocupacionales de obreros
sindicalizados en cierto sector de la construcción. Determine cuál es la
ocupación en la que existe la mayor variación en
los salarios básicos y cuál es la que muestra la
menor variación. Para hacer estas comparaciones
deberá utilizar el coeficiente de
variación.

Salarios básicos por hora,
según tipo de trabajo y lugares
encuestados

Francisco Antonio Cabrera
González

f_cabrera51[arroba]hotmail.com

Graduado en mayo de 1980 de Economista-Organizador de la
Producción Agrícola y Master en
Ciencias
Económicas en la Academia Agrícola K. A. Timiriazev
de Moscú –Rusia.

Profesor de la Universidad de
Panamá
desde 1981. Ha ejercido la docencia
universitaria en los Centros Regionales de Azuero
(Chitré), Los Santos, Veraguas, Coclé y San
Miguelito. Catedratico (Profesor Regular) desde 1991 del
Departamento de Estadística Económica y Social de
la Facultad de Economía.

En su vida universitaria, como docente, ha sido
representante de los profesores del CRU-Azuero (Chitré)
ante el Consejo General Universitario -CGU (1990-1992),
Vicepresidente de la Asociación de Profesores de la
Universidad de Panamá –APUDEP (1991-1993),
Presidente de la APUDEP (1993-1995), Director del Centro Regional
Universitario de San Miguelito –CRUSAM (1995-2000) y en la
actualidad es docente investigador de la Universidad de
Panamá.

UNIVERSIDAD DE PANAMÁ

CENTRO REGIONAL UNIVERSITARIO DE SAN
MIGUELITO

FACULTAD DE ECONOMÍA

DEPARTAMENTO DE ESTADÍSTICA ECONÓMICO Y
SOCIAL

Curso: Est.115 : "Estadística Económica
I".