Método prehistórico para obtener la raíz cuadrada de un número (página 2)
Por lo que se dividiría el 34 entre el
4
Y vienen las enseñanzas de la
división:
34 entre 4 a 8 4×8= 32 pero por las que se lleven: a
7
Y este se colocaría junto al 2

aquí viene otro secreto ese mismo número
se pone en la segunda línea y si surge otra pregunta de
¿porqué? Será la misma respuesta.

nos olvidamos del 2 y procedemos a multiplicar el 7 por
el 47 de la segunda línea
7 x 7 = 49 se pone el nueve bajo el 6 y llevamos
4

después; 7 x 4 = 28 más los 4 que llevamos
son 32

y realizamos la resta correspondiente.

YA ESTUVO
RAIZ CUADRADA DE 746 ES 27 CON RECIDUO 17
Para comprobarla se multiplicaría 27 por si
mismo
Porque recordemos que la raíz cuadrada es la
operación inversa de elevar al cuadrado un
número.
27 x 27 = 729
y se le agrega el residuo quedando
729 + 17 = 746
EJEMPLO 2: número de 4 cifras.
Obtener la raíz cuadrada de 6938
le ponemos ya nuestro conocido dibujito.

a continuación se separa el número en
cifras pares comenzando de derecha a izquierda
quedando:

y se busca un número que multiplicado por si
mismo de cercano a 69
siendo 8

8 x 8 = 64

se realiza la resta correspondiente

Se duplica el 8 en la segunda línea
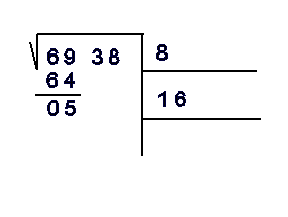
se baja el siguiente periodo

Al encontrar el siguiente número serán
tres en la segunda línea, por lo que se buscará un
número que el uno del dieciséis divida al
5
Por lo que será el 3

Segundo secreto se pone también en la segunda
línea

En el número 83 nos olvidamos del 8 y
multiplicamos el 3 por el número de abajo

Realizamos la resta correspondiente

YA ESTUVO
Raíz cuadrada de 6938 es igual a 83 con residuo
49
Para comprobarla se multiplica 83 por 83 o sea que se
eleva al cuadrado
Dando 6889
Se le agrega el residuo 6889 + 49 igual a
6938
Espero haber sido claro, claro que si hay alguna duda
estamos a sus órdenes.
Profesor Luis Benjamín Flores
Isaac
Escuela Urbana Nº 164 Col San
Andrés
Guadalajara, Jalisco, México
Profesor Jubilado en Educación Primaria
por 34 años, Habiendo atendido principalmente los grados
de quinto y sexto de Educación Primaria.
Actualmente Estudiante de la Maestría en
Tecnologías para el Aprendizaje en
la U. de G.
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |