Ángulos ? Geometría (página 2)

Enviado por gatsby_morgado

Partes: 1, 2

Convexo, es el que vale más que un
llano.

Ángulos suplementarios, son los que
sumados valen 180º, es decir, un ángulo
llano.

Cada ángulo se llama suplemento del otro.
Así el ángulo es el suplemento del ángulo y viceversa.

Ángulos complementarios, son los que
sumados valen 90º, es decir, un ángulo
recto.

Ángulos consecutivos, son los que tienen
un mismo vértice y un lado común.

Los ángulos y
tienen un mismo vértice común, O, y un lado
común, .

Ángulos adyacentes, son ángulos
consecutivos cuyos lados no comunes están en línea
recta.

Los ángulos adyacentes son suplementarios, porque
juntos equivalen a un ángulo llano
(180º).

Los ángulos y
son adyacentes.

Ángulos opuestos por el vértice,
son los ángulos en que los lados del uno son
prolongaciones opuestas de los lados del otro.

También se dice que son aquellos cuyos lados son
semirrectas opuestas.

El instrumento para medir un
ángulo en grados sexagesimales se denomina
transportador

y es un medio círculo graduado con doble escala, una de
0º a 180º y la otra de 180º a
0º.

Para medir un ángulo, se coloca el punto central
del transportador sobre el vértice del ángulo y uno
de los lados debe coincidir con la línea del
cero.

Ángulo inscrito: Es aquel cuyo
vértice está sobre la circunferencia y cuyos lados
son secantes. La amplitud de un ángulo inscrito equivale a
la mitad de la amplitud del arco que abarca.

Características de los ángulos
inscritos:

Dos ángulos inscritos en cada uno de los arcos
que una cuerda determina son suplementarios.

Todos los ángulos inscritos que abarcan un
mismo arco son iguales.

En una misma circunferencia, los arcos cortados por
paralelas son iguales.

Todo ángulo inscrito en una semicircunferencia
es recto.

Angulo semiinscrito: Es aquel cuyo vértice
está sobre la circunferencia, uno de sus lados es tangente
y el otro, secante. Al igual que en el inscrito, su amplitud
equivale a la mitad de la amplitud del arco que
abarca.

Ángulo interior: es aquel cuyo
vértice está en el interior de la circunferencia.
La amplitud de un ángulo interior equivale a la semisuma
de los arcos que abarca éste, y su opuesto por el
vértice.

Angulo exterior es aquel cuyo vértice es
exterior a la circunferencia y sus lados, secantes. La amplitud
de un ángulo exterior equivale a la semidiferencia de la
amplitudes de los arcos abarcados por él.

Angulo central es aquel que su vértice
está en el centro de la circunferencia. Por
definición, su amplitud coincide con el arco que
abarca.

Triángulo:

Es la porción del plano limitada por tres
rectas que se cortan dos a dos.

Características:

Todo triángulo consta de 3 vértices que
son las intersecciones de las rectas.
Los segmentos que unen los vértices se llaman
lados del triángulo.
Los lados del triángulo forman tres
ángulos que se llaman ángulos internos del
triángulo.
En todo triángulo los ángulos internos
suman 180º.
En todo triángulo, un lado es menor que la
suma de los otros dos lados y mayor que su
diferencia.

Altura de un Triángulo: La altura de un
triángulo es el segmento perpendicular que va
desde un vértice al lado opuesto o a la
prolongación de éste.

Se llama base del triángulo al lado sobre
el que se apoya.

Clasificación de los
triángulos

En relación a los lados:

Equilátero, el que tiene los tres lados
iguales

Isósceles, el que tiene dos lados
iguales y el otro desigual

Escaleno, el que tiene los tres lados
desiguales.

Clasificación en relación a sus
ángulos:

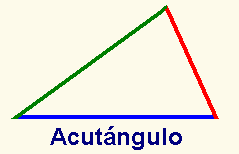
Acutángulo, el que tiene todos sus
ángulos agudos, es decir, menores de
90º

Obtusángulo, el que tiene algún
ángulo obtuso, es decir mayor a
90º

Rectángulo, el que tiene un
ángulo recto, es decir, un ángulo que mide
90º. Los dos lados que forman el ángulo recto se
llaman catetos y el otro hipotenusa.

Área de un Triángulo:

El área de un triángulo es igual
a la mitad del producto de
la longitud de la base por la altura relativa a
dicha base.

Baricentro

Es el punto de intersección de las medianas de un
triángulo, entendiendo por mediana la recta que
parte de un vértice para ir al punto medio del lado
opuesto.

Circuncentro

Es el punto de intersección de las mediatrices de
un triángulo, entendiendo por mediatriz la recta
que es perpendicular al lado en su punto medio.

Ortocentro

Es el punto de intersección de las alturas de un
triángulo, entendiéndose por altura la recta
que parte de un vértice para ser perpendicular al lado
opuesto.

Incentro

Es el punto de intersección de las bisectrices
interiores de un triángulo, entendiendo por
bisectriz la recta que parte de un vértice y divide
el ángulo en dos partes iguales.