- Sistema
binario - Sistema octal
- Sistema
decimal - Sistema
hexadecimal - Conversiones
numéricas - Bit
- Byte- kilobyte- gigabyte-
terabyte - Conversión de bit,
byte, kilobyte, megabyte y terabyte - Unidades de
medidas - Software
libre - Software libres
actuales - Conclusión
- Recomendaciones
- Bibliografía
- Anexos
La informática es importante ya que nos sirve
de base para el desarrollo y
desenvolvimiento verbal y practico en esta área, este
básicamente se trata del software en general, partes
y sistemas que lo
conforman.
El hombre en su
vida cotidiana trabaja desde el punto de vista numérico
con el sistema decimal y
desde el punto de vista alfabético con un determinado
idioma. Asimismo, la computadora
debido a su construcción, lo hace desde ambos puntos de
vista con el sistema
binario, utilizando una serie de códigos que permiten
su perfecto funcionamiento.
Tanto el sistema decimal como el binario están
basados en los mismos principios. En
ambos, la representación de un número se
efectúa por medio de cadenas de símbolos, los cuales representan una
determinada cantidad dependiendo del propio símbolo y de
la posición que ocupa dentro de la cadena.
Los sistemas de
numeración que utiliza la computadora
son: El Sistema Binario, el Decimal, el Octal y el
Hexadecimal.
En el presente trabajo se
estudiarán los siguientes puntos: Sistemas de
numeración, las unidades de información y medida, así como, el
software
libre, su utilidad,
características y algunos tipos como el Colibrí y
el Linux. Todos
estos con el objetivo de
poder
garantizar al lector el libre entendimiento y comprensión
a la hora de manejar un sistema informático.
CONTENIDO
Es un sistema de numeración que
utiliza internamente hardware de las computadoras
actuales. Se basa en la representación de cantidades
utilizando los dígitos 1 y 0, por tanto su base es dos
(numero de dígitos de sistemas). Cada digito de un numero
representado en este sistema se representa en BIT
(contracción de binary digit).
Los ordenadores trabajan internamente con dos
niveles de voltaje, por lo que su sistema de numeración
natural es el sistema binario (encendido '1', apagado
'0').
Es un sistema de numeración cuya base es 8
, es decir, utiliza 8 símbolos para la
representación de cantidades . Estos sistemas es de los
llamados posiciónales y la posición de sus cifras
se mide con la relación a la coma decimal que en caso de
no aparecer se supone implícitamente a la derecha del
numero. Estos símbolos son:
0 1 2 3 4 5 6 7
Los números octales pueden construirse a partir
de números binarios agrupando cada tres dígitos
consecutivos de estos últimos (de derecha a izquierda) y
obteniendo su valor
decimal.
Por ejemplo, el número binario para 74 (en
decimal) es 1001010 (en binario), lo agruparíamos como 1
001 010. De modo que el número decimal 74 en octal es
112.
En informática, a veces se utiliza la
numeración octal en vez de la
hexadecimal. Tiene la ventaja de que no
requiere utilizar otros símbolos diferentes de los
dígitos.
Es posible que la numeración octal se usara
en el pasado en lugar de la
decimal, por ejemplo, para contar los
espacios interdigitales o los dedos distintos de los pulgares.
Esto explicaría porqué en latín nueve
(novem) se parece tanto a nuevo (novus). Podría
tener el significado de número nuevo.
Es uno de los sistema denominado
posiciónales, utilizando un conjunto de símbolos
cuyo significado depende fundamentalmente de su posición
relativa al símbolo, denominado coma (,) decimal que en
caso de ausencia se supone colocada a la derecha. Utiliza como
base el 10, que corresponde al número del símbolo
que comprende para la representación de cantidades; estos
símbolos son:
0 1 2 3 4 5 6 7 8 9
Este conjunto de símbolos se denomina
números árabes. Es el
sistema de numeración usado habitualmente en todo el mundo
(excepto ciertas culturas) y en todas las áreas que
requieren de un sistema de numeración. Sin embargo
contextos, como por ejemplo en la informática, donde se
utilizan sistemas de numeración de propósito
más específico como el
binario o el
hexadecimal.
El sistema decimal es un sistema de
numeración posicional, por lo que el valor del
dígito depende de su posición dentro del
número. Ejemplo:
Es un sistema posicional de numeración en
el que su base es 16, por tanto, utilizara 16 símbolos
para la representación de cantidades. Estos
símbolos son:
0 1 2 3 4 5 6 7 8 9 A B C D E
F
Su uso actual está muy vinculado a la
informática. Esto se debe a que un dígito
hexadecimal representa cuatro dígitos binarios (4
bits = 1
nibble); por tanto, dos dígitos
hexadecimales representan ocho dígitos binarios (8
bits = 1
byte, (que como es sabido es la unidad
básica de almacenamiento de
información).
Dado que nuestro sistema usual de
numeración es de base decimal, y por ello sólo
disponemos de diez dígitos, se adoptó la
convención de usar las seis primeras letras del alfabeto
latino para suplir los dígitos que nos faltan: A = 10, B =
11, C = 12, D = 13, E = 14 y F = 15. Como en cualquier sistema de
numeración posicional, el valor numérico de cada
dígito es alterado dependiendo de su posición en la
cadena de dígitos, quedando multiplicado por una cierta
potencia de la
base del sistema, que en este caso es 16.
Por ejemplo:
3E0,A16 =
3×162 + E×161 +
0×160 + A×16-1 = 3×256 +
14×16 + 0×1 + 10×0,0625 = 992,625.
Conversión de binario a
decimal
El sistema de numeración binario es un
sistema de posición donde cada dígito binario (bit)
tiene un valor basado en su posición relativa al LSB.
Cualquier número binario puede convenirse a su equivalente
decimal, simplemente sumando en el número binario las
diversas posiciones que contenga un 1.
Ejemplo: Cómo cambiar el número
binario 11012 al sistema decimal.
11012
= 1
x 23 + 1 x 22
+ 0 x 21
+ 1 x 20
= 1 x 8 + 1 x 4 + 0 x 2 + 1 x 1
=
8 + 4 + 0 + 1
= 13
Resultado
11012 = 1310
Conversión de decimal a
binario
Para cambiar un número decimal a número
binario, se divide el número entre dos. Se escribe
el cociente y el residuo. Si el cociente es mayor de uno,
se divide el cociente entre dos. Se vuelve a escribir el
cociente y el residuo. Este proceso se
sigue realizando hasta que el cociente sea cero. Cuando el
cociente es cero, se escribe el cociente y el residuo. Para
obtener el número binario, se escribe cada uno de los
residuos comenzando desde el último hasta el primero de
izquierda a derecha, o sea, el primer residuo se escribe a la
izquierda, el segundo residuo se escribe a la derecha del primer
residuo, y así sucesivamente.
Ejemplo:
Cómo cambiar el número 10 del sistema
decimal al sistema binario

Bit es el acrónimo de Binary digit.
(dígito binario). Un bit es un dígito del
sistema de numeración
binario.
El bit es la unidad mínima de información
empleada en informática, en cualquier dispositivo digital,
o en la
teoría de la información.
Con él, podemos representar dos valores
cualesquiera, como verdadero o falso, abierto o cerrado, blanco o
negro, norte o sur, masculino o femenino, amarillo o azul, un
nervio estimulado o un nervio inhibido. (Sabemos que no todo lo
que se encuentra en nuestro universo es
blanco o negro, pero aún así podemos utilizar esta
forma binaria de representación para expresar estados
intermedios logrando la precisión deseada), etc. Basta con
asignar uno de esos valores al estado de
"apagado" (0), y el otro al estado de "encendido" (1).
Podemos imaginarnos un bit como una bombilla que
puede estar en uno de los siguientes dos estados:

Se describe como la unidad básica de
almacenamiento de información, generalmente equivalente a
ocho
bits (01011101), pero el tamaño del byte
depende del
código de caracteres o código
de información en el que se defina.
KILOBYTE
Un kilobyte (pronunciado /kilobáit/) es
una unidad de medida común para la capacidad de memoria o
almacenamiento de las computadoras. Es equivalente a 1024 (o
210)
bytes. Generalmente se abrevia como KB, K, kB,
Kbyte o k-byte. Las
PC de
IBM más antiguas, por ejemplo,
tenían una capacidad máxima de 640 K, o alrededor
de 640 000 caracteres de datos.
MEGABYTE
El Megabyte (MB) es una unidad de medida de cantidad de
datos informáticos. Es un múltiplo binario
del
byte, que equivale a 220 (1 048 576)
bytes, traducido a efectos prácticos como 106
(1 000 000) bytes.
GIGABYTE
Un gigabyte (de símbolo GB ó GiB) es una
unidad de medida informática equivalente a mil millones
de
bytes (no confundir con el billón
americano). Dado que los ordenadores trabajan en base binaria, en
lugar de que un gigabyte sea 10³
megabytes (1000 MiB), el término
gigabyte significa 210 megabytes (1024 MiB). Pero si
somos exactos, 1 GB son 1.073.741.824 bytes ó 1.024 MB. En
este último caso, puede ser abreviado como GiB
(recomendado) ó GB
TERABYTE
Una unidad de almacenamiento tan desorbitada que resulta
imposible imaginársela, ya que coincide con algo
más de un trillón de bytes. Un uno seguido de
dieciocho ceros. Su símbolo es el TB y es equivalente a
240
bytes.
Debido a irregularidades en la definición y uso
del
Kilobyte, el número exacto
de
bytes en un Terabyte en la práctica,
podría ser cualquiera de los siguientes
valores:
- 1,000,000,000,000 bytes – 1012. Esta
definición es la que se usa en el contexto general
cuando se refiere a almacenamiento en
discos,
redes u otro hardware. - 1,099,511,627,776 bytes – 10244 o
240. Esto es 1024 veces un
Gigabyte (un Gigabyte 'binario'). Esta
es la definición mas usada en las ciencias
de la computación (computer science) y en
programación (computer programming) y,
la mayor parte del software, emplea también
ésta definición.
CONVERSION
DE BIT, BYTE, KILOBYTE, MEGABYTE Y TERABYTE

- Hz
El hercio es la unidad de frecuencia del
Sistema Internacional de Unidades. Proviene del apellido del
físico alemán Heinrich Rudolf Hertz, descubridor de
la transmisión de las ondas
electromagnéticas. Su símbolo es hz. (que se
escribe sin punto). En
inglés se llama hertz (y se
pronuncia /jérts/).
Un hercio representa un ciclo por cada segundo,
entendiendo ciclo como la repetición de un
evento.
Un hertzio significa simplemente "uno por segundo
" (1/s); 100 medios "ciento
del hertzio por segundo", etcétera. La unidad se puede
aplicar a cualquier acontecimiento periódico
– por ejemplo, un reloj se pudo decir para hacer tictac en 1
hertzio, o un corazón
humano se pudo decir para batir en 1,2 hertzios. La frecuencia de
acontecimientos aperiódicos, tales como radiactivo se
decae, se expresa en becquerels .
Para evitar la confusión, los ángulos
periódicamente que varían no se expresan
típicamente en hertzios, sino algo en una unidad angular
apropiada tal como radianes por segundo. Un disco que rota en 1
revolución
por el minuto (RPM) se puede decir así para rotar en 0,105
rad/s o 0,017 hertzios, donde el último refleja el
número de revoluciones completas por
segundo.
Ejemplo:
En los Estados Unidos,
el suministro común de energía doméstica es
a 60 hertzios (lo que significa que la corriente cambia de
dirección o polaridad 120 veces, o 60
ciclos, cada segundo).
En Europa, la
frecuencia de línea es de 50 hertzios, o 50 ciclos por
segundo, la transmisión de radio se realiza
a tasas de frecuencia mucho mayores, habitualmente expresadas en
kilohertzios (KHz) or megahertzios (MHz).
- Megahertz
Megahertzio, múltiplo del hertzio igual a 1
millón de hertzios. Utilizado para medir la
"velocidMegahertzios, es una medida de frecuencia (número
de veces que ocurre algo en un segundo). En el caso de los
ordenadores, un equipo a 200 MHz será capaz de dar 200
millones de pasos por segundo.
En la velocidad real
de trabajo no sólo influyen los MHz, sino también
la arquitectura
del procesador (y el
resto de los componentes); por ejemplo, dentro de la serie X86,
un Pentium a 60 MHz
era cerca del doble de rápido que un 486 a 66 MHzad bruta"
de los microprocesadores.
Ejemplo:
Si usted mira el dial de un receptor de radio,
encontrará que lleva una indicación de frecuencias
o longitudes de onda. La mayoría de los receptores tienen
varias bandas de ondas y éstas pueden ser seleccionadas
por medio de un botón llamado comúnmente el
"selector de bandas de ondas", que le ofrece a usted una
elección, por ejemplo, entre la banda de onda media
(emisoras standard), la de la onda corta, o bandas de onda corta
y la banda FM.
Cada una de estas bandas del receptor pertenece a una de
las asignaciones oficiales de bandas de frecuencias. La banda
entre 3 y 30 kHz se denomina banda VLF (de Muy Baja Frecuencia)
(1Hz (Hertzio) es 1 ciclo por segundo, 1 kHz (Kilohertzio) es
1000 c/s, 1 MHz (Megahertzio) es 1.000.000 c/s).
El margen de 30 – 300 kHz recibe el nombre de banda de
Baja Frecuencia en la cual se encuentran las emisoras de
radiodifusión de onda larga; la banda de 300 – 3.000 kHz
es la de la frecuencia media; entre 3.000 y 30.000 kHz es decir,
entre 3 y 30 MHz, hallamos la banda de alta frecuencia, mejor
conocida como banda de onda corta, donde los equivalentes
métricos de las frecuencias se extienden entre 100 y 10
metros. Por encima de 30 MHz está la banda de VHF (Muy
Alta Frecuencia); por encima de 300 MHz se habla de banda de
Ultra Alta Frecuencia (UHF)
- Nanosegundo
Un nanosegundo es la milmillonésima parte de un
segundo, 10-9. Es decir, en un segundo hay
1.000.000.000 de nanosegundos. Se trata de una escala de
tiempo muy
pequeña, pero bastante común en los ordenadores,
cuya frecuencia de proceso es de unos cientos de
Megahercios.
Decir que un procesador es de 500 Mhz, es lo mismo que
decir que tiene 500.000.000 ciclos por segundo, o que tiene un
ciclo cada 2 ns.
Ejemplo:
Este tiempo tan corto no se usa en la vida diaria, pero
es de interés en
ciertas áreas de la física, la química y en la
electrónica. Así, un nanosegundo es
la duración de un ciclo de reloj de un procesador de 1
GHz, y es también el tiempo que tarda la luz en recorrer
aproximadamente 30 cm.
- Milisegundo
Un milisegundo es el período de tiempo que
corresponde a la milésima fracción de un segundo
(0,001s).
- Microsegundo
Es una Unidad de tiempo, equivalente a una
milésima parte de un segundo. (ms).
Ejemplo:
Numerosas personas, no obstante, se han dado cuenta de
que en 49.7 días hay 4294080000 milisegundos. Esa cifra es
muy semejante a 2^32 = 4294967296.
En otras palabras, un registro de 32 bits podría contar
4294967296 milisegundos o, lo que es lo mismo, 49'7103
días (exactamente, 49 días, 17 horas, 2 minutos y
47'296 segundos).
Software libre (en inglés
free software) es el software que, una vez obtenido, puede
ser usado, copiado, estudiado, modificado y redistribuido
libremente. El software libre suele estar disponible
gratuitamente en Internet, o a precio del
coste de la distribución a través de otros
medios; sin embargo no es obligatorio que sea así y,
aunque conserve su carácter de libre, puede ser vendido
comercialmente. Análogamente, el software gratis o
gratuito (denominado usualmente
Freeware) incluye en algunas ocasiones el
código fuente; sin embargo, este tipo de software no es
libre en el mismo sentido que el software libre, al
menos que se garanticen los derechos de
modificación y redistribución de dichas versiones
modificadas del programa.
No debemos confundir software libre con software de
dominio
público. El término inglés free es
ambiguo, y puede refererirse tanto a la libertad
(free speech, libertad de expresión) como a la
gratuidad (free beer, cerveza gratis).
En español no
existe tal ambigüedad, distinguiéndose claramente el
software libre (objeto del presente artículo) del
software gratis o gratuito (freeware).
El freeware suele incluir una
licencia de uso, que permite su
redistribución pero con algunas restricciones, como no
modificar la aplicación en sí, ni venderla, y dar
cuenta de su autor. También puede desautorizar el uso en
una compañía con fines comerciales o en una entidad
gubernamental.
Algunos desarrolladores liberan versiones freeware de
sus productos para
obtener un número de seguidores que puedan estar
dispuestos a pagar por una versión más completa, o
porque es una edición
obsoleta de un programa.
Otros lo hacen porque no consideran que ese programa
pueda generar una ganancia económica, o porque creen en el
valor de ofrecer algo gratis.
Contrariamente a lo que se cree, los programas de
software libre no necesariamente son freeware. Esto usualmente
deriva de una confusión sobre el significado de la palabra
free en inglés, que puede ser tanto gratis
como libre, es decir, un tipo de software cuya licencia
autoriza su uso, modificación y redistribución con
y sin cambios.
Otros tipos de licencias de distribución de
software son
shareware,
postcardware,
donationware o
abandonware, entre otros.
- LYNUX:
Desarrollado por: Equipo Interdisciplinario
Tipo de Recurso: Articulo.
Tipo de Destinatario: General
Tipo Acceso (costo):
Libre – Gratuito – Fuente Abierta – GNU
Este documento aborda las distintas formas en las que
se puede utilizar un ordenador de Linux sin dañar el
medioambiente. Para ello se propone poner en práctica
sus funciones y
así ahorrar papel y energía.
Puesto que Linux no necesita un hardware complejo, se
puede utilizar en computadores no tan modernos y así
prolongará la duración de
éstos.
Se podrán usar juegos para
desarrollar la
educación medioambiental y un software que estimule
los procesos
ecológicos.
- COLIBRÍ
Desarrollado por: Comunidad de
Usuarios de Software Libre en Colombia
Tipo de Recurso: Sitio Web
Tipo de Destinatario: General
Tipo Acceso (costo): Libre – Gratuito – Fuente Abierta
– GNU
Colibrí es una organización democrática que busca
reunir a los interesados en el software libre en Colombia:
Documentos,
eventos y
noticias
sobre este tipo de programas en Colombia.
En la sección documentos encontrará un
listado de preguntas frecuentes sobre el uso de software libre,
así como el proyecto de
ley que se esta
impulsando en este país.
El sistema de numeración es el conjunto de
símbolos utilizados para la representación de
cantidades, así como las reglas que rigen dicha
representación. En la informática se usaron muchos
sistemas de numeración como lo fue el sistema binario,
decimal, octal y hexadecimal ya que fueron muy útil para
la realización de varios programas pero la tecnología ha
avanzado tanto que ya estos sistemas están si se puede
decir obsoleto.
- El sistema decimal que es uno de los denominados
sistemas posicionales. - El Sistema binario que utiliza internamente el
hardware de las computadoras actuales. - El sistema de numeración Octal cuya base es
8 - El hexadecimal que utiliza 16 símbolos para la
representación de cantidades.
Para la realización de estos programas se tenia
que realizar algunas conversiones numéricas que son de
decimal-binario (se divide el número entre dos) y
binario-decimal (se suma en el número binario las diversas
posiciones que contengan 1).
En cuanto al software libre suele estar disponible
gratuitamente en Internet, o a precio del coste de la
distribución a través de otros medios; sin embargo
no es obligatorio que sea así y, aunque conserve su
carácter de libre, puede ser vendido comercialmente. Una
vez obtenido, puede ser usado, copiado, estudiado, modificado y
redistribuido libremente.
Existen diversos tipos de software
libre entre ellos están el colibrí y el
Lynux.
- Desde cualquier sistema de conversión es
más fácil pasarlo a binario y luego al sistema
asignado. - Conocer un poco o a cabalidad sobre los
términos informáticos más comentados en el
día a día como hertz byte. Más si estudias
la carrera como tal. - Tener en cuenta que la migración hacia el software libre no es
un proceso sencillo hay que tomar las medidas necesarias para
el adiestramiento del personal y su
capacitación para el buen desempeño del sistema. - Al implementar el software libre deberían
tomar en cuenta el soporte que exista para los diferentes
programas utilizados actualmente, como son el caso del Autocad,
Saint, etc.
- www.google.com
- www.monografias.com
- www.elrincondelvago.com
- www.lawebdelprogramador.com/diccionario
- www.wikipedia.org/wiki/linux
- www.escolar.com
Sistema Binario
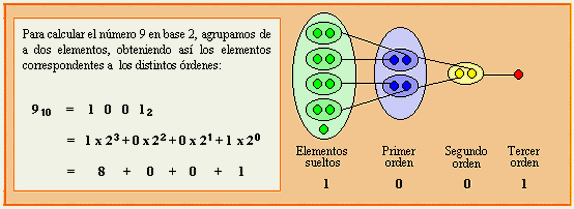
Tabla de multiplicación
Hexadecimal

Ejemplos de
Conversiones (Sistema Decimal al Sistema
Binario)
Ejemplo 1: Cómo cambiar el
número 23 del sistema decimal al sistema
binario.

Ejemplo 2: Cómo cambiar el
número 378 del sistema decimal al sistema
binario.

Ejemplos de Conversiones (Sistema
Binario al Sistema Decimal)
Ejemplo 1: Cómo cambiar el
número binario 111112 al sistema
decimal.
111112 = 1 x 24 + 1 x 23 + 1 x 22 + 1 x 21 + 1 x 20
= 1 x 16 + 1 x 8 + 1 x 4 + 1 x 2 + 1 x 1
= 16 + 8 + 4 + 2 + 1
= 31
Resultado
111112 = 3110
Ejemplo 2: Cómo cambiar el
número binario 1010102 al sistema
decimal.
1010102 = 1 x 25 + 0 x 24 + 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20
= 1 x 32 + 0 x 16 + 1 x 8 + 0 x 4 + 1 x 2 + 0 x 1
= 32 + 0 + 8 + 0 + 2 + 0
= 42
Resultado
1010102 = 4210
Combinaciones con dos
Bits

- 0 0 – los dos están
"apagados" - 1 0 – el primero está "encendido" y el
segundo "apagado" - 0 1 – el primero está "apagado" y el
segundo - 1 1 – los dos están "encendidos"
"encendido" - 0 0 – los dos están
"apagados" - 1 0 – el primero está "encendido" y el
segundo "apagado" - 0 1 – el primero está "apagado" y el
segundo - 1 1 – los dos están "encendidos"
"encendido"


SOFTWARE LIBRE ACTUAL
(LINUX)

SOFTWARE LIBRE ACTUAL
(COLIBRI)

Ylenis Gittens