Introducción al estudio de los circuitos lógicos y sistemas numéricos (página 2)
RESTA EN COMPLEMENTO A DOS.
La resta en complemento a dos resuelve el problema de
esta operación con los signos. Por
ejemplo, el sustraendo negativo y minuendo positivo produce un
resultado positivo; la resta de dos números A y B
negativos puede dar resultados positivos o negativos. Para
realizarla se procede con la fórmula definida de la
siguiente forma:
![]()
(Ec.1.5); La diferencia de dos números, A menos
B es equivalente a la suma de A más el
complemento a dos de B.
I) Resta de dos números positivos.
El resultado puede presentar varias formas que se determinan con
los siguientes casos:
(A mayor o igual que B):

De está manera, el resultado queda en forma
binaria normal y es igual a valor del 17vo
bit no se toma en cuenta para el resultado. En decimal
A=2375110 y B=1518610;
entonces A-B=856510 =
00100001011101012
(A menor que B):

De está manera, el resultado es negativo y queda
en forma de complemento a dos, el acarreo del 17vo bit no se toma
en cuenta. Sin embargo, para saber el verdadero valor, el
resultado se debe complementar a dos. Este es un número
binario negativo de 16 bits, lo cual tiene un valor de: ![]() . En decimal la
. En decimal la
operación se efectúa: A = 774810
y B = 3115110 entonces el resultado es A-B =
-2340310.
II) RESTA DE DOS NÚMEROS NEGATIVOS Y DE
DISTINTO SIGNO. El resultado puede presentar varias formas
que se determinan aplicando los mismos casos de la suma en
formato de 16 bits.
Tabla 1. 3. Resumen de las operaciones suma
y resta binaria con los datos A y B,
utilizando el formato de 16 bits.
Operación | Acarreo 17vo bit | Acarreo 16vo | Resultado | Observaciones | ||
A+B A>0; B>0 | 0 | 0 | Positivo en binario | Chequear para no exceder el | ||
A+B A>0; B<0 (**) | 0 | 1 | Negativo en complemento a | Complementar los 16 bits para | ||
A+B A<0; B>0 (**) | 1 | 0 | Positivo en binario | El 17vo bit no se toma en cuenta | ||
A+B A<0; B<0 | 1 | 1 | Negativo en complemento a | Complementar los 16 bits para Chequear para no exceder el | ||
A-B A>0; B>0 A>=B | 1 | 0 | Positivo en binario | El 17vo bit no se toma en cuenta | ||
A-B A>0; B>0 A<B | 0 | 1 | Negativo en complemento a | Complementar los 16 bits para | ||
A-B A>0; B<0 | 0 | 0 | Positivo en binario | Chequear para no exceder el | ||
A-B A<0; B>0 |
1 | 1 | Negativo en complemento a | Complementar los 16 bits para Chequear para no exceder el | ||
A-B A<0; B<0 (**) | 0 | 1 | Negativo en complemento a dos o | Complementar los 16 bits para | ||
| (**) Se producen resultados | |||||
REPRESENTACIÓN NUMÉRICA EN COMA FIJA Y
COMA FLOTANTE.
Estas representaciones son utilizadas por las computadoras
para procesar cálculos numéricos con formatos
grandes. Consiste en una cadena de bits que guardan
relación con la notación científica, y
pueden representar números enteros y números reales
tanto negativos como positivos. Los formatos más conocidos
son la coma fija y la coma flotante, también denominados
punto fijo y punto flotante respectivamente. Antes de comenzar a
describir estos formatos se debe entender el funcionamiento de un
caso especial de complemento a dos el cual se denomina
representación con exceso o sesgada.
REPRESENTACIÓN CON EXCESO O
SESGADA.
Son representaciones para números con signo que
eliminan el centrado de la representación básica en
complemento a dos. Por ejemplo para indicar números
decimales desde un valor numérico -P10
hasta +P10 es necesario desplazar el
equivalente binario (-P10 )2
sumando P2 unidades positivas. Esta cantidad se
conoce como exceso o sesgo. Las representaciones con exceso se
utilizan, con frecuencia, para representar los exponentes de los
números con coma flotante. En la tabla 1.4 se pueden
observar las representaciones desde -810 hasta
+810 en complemento a dos y en código
con exceso donde P2 = 10002.
En complemento a dos -810 es igual a
10002. Sin embargo, la representación
del mismo número negativo en código desplazado con
exceso 8 es de 00002; es de hacer notar
que solamente ocurre un cambio en el
bit más significativo (MSB: Most Significative Bit) del
código con exceso. Por lo tanto, la representación
de cualquier código con exceso -P, para indicar
números negativos, se forma sumando el valor de P a
cada palabra o número del código.
COMPARACIÓN DE CÓDIGOS
EN COMPLEMENTO A DOS Y EXCESO 8.
DECIMAL | COMPLEMENTO A | EXCESO 8 |
+7 | 0111 | 1111 |
+6 | 0110 | 1110 |
+5 | 0101 | 1101 |
+4 | 0100 | 1100 |
+3 | 0011 | 1011 |
+2 | 0010 | 1010 |
+1 | 0001 | 1001 |
0 | 0000 | 1000 |
-1 | 1111 | 0111 |
-2 | 1110 | 0110 |
-3 | 1101 | 0101 |
-4 | 1100 | 0100 |
-5 | 1011 | 0011 |
-6 | 1010 | 0010 |
-7 | 1001 | 0001 |
-8 | 1000 | 0000 |
REPRESENTACIÓN NUMÉRICA EN COMA
FIJA.
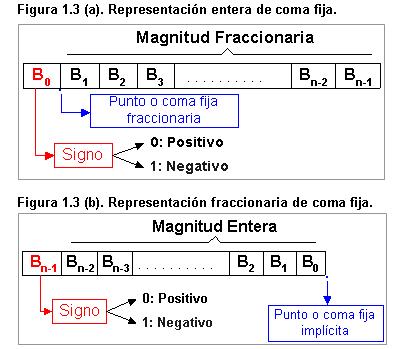
Los números fraccionarios y
con signo se pueden representar mediante la coma fija; ejemplo de
esto se puede apreciar en la tabla 1.2 y la figura 1.3(a) donde
se tiene la representación de números enteros con
signo en formato de 16 bits. No obstante, existe otra
representación para coma fija, la cual consiste en fijar
la posición de la coma después del bit de signo;
ver figura 1.3(b) respectivamente. Los restantes bits deben
indicar la magnitud fraccionaria.
REPRESENTACIÓN NUMÉRICA EN COMA
FLOTANTE.
Los números representados en coma flotante
tienen la misma forma que la notación científica.
La representación tiene la siguiente forma
![]()
(Ec.1.6); donde M es la mantisa o
significado y se representa en coma fija, este valor indica la
cantidad de dígitos significativos que tiene el
número N de coma flotante. El valor
E es el exponente o característica,
también de coma fija; está dado en formato de
complemento a dos con exceso y b es la base del
sistema. En forma
general, de la Ec.1.1 se puede obtener la
representación con signo de coma fija y está dada
por: ![]() , ahora
, ahora
sustituyendo por el formato de coma fija, dada en la figura
1.3(b), se obtiene la forma de coma flotante
![]()
![]()
(Ec.1.7). La fórmula general queda del siguiente
modo;
![]()
(Ec.1.8)
donde bs es el bit de signo,
e es el número de bits del exponente con
![]() ; esto es
; esto es
equivalente a escribir E con formato de exceso en
base dos de la siguiente manera; ![]() , por lo tanto,
, por lo tanto, ![]()
Existen varias formas de representar los formatos de
coma flotante; sin embargo, los que más se utilizan son
los siguientes:
En las figuras 1.4(a) y 1.4(b) se definen los formatos
en coma flotante para datos numéricos reales cortos y
largos utilizados en los computadores.

La tabla 1.5 muestra un
resumen de los formatos de precisión sencilla y doble
(corto y largo) respectivamente; usados en los sistemas de
computación.
FORMATO | TOTAL DE | BITS DE LA | BITS DEL | EXCESO DEL |
Estándar | ||||
754-1985 | ||||
Precisión | 32 | 24 | 8 | 128 |
Doble Precisión | 64 | 53 | 11 | 1024 |
IBM 360 | ||||
Precisión | 32 | 24 | 7 | 64 |
Doble precisión | 64 | 56 | 7 | 64 |
DEC VAX 11/780 | ||||
Formato F | 32 | 24 | 8 | 128 |
Formato D | 64 | 56 | 8 | 128 |
Formato G | 64 | 53 | 11 | 1024 |
Tabla 1.5. Formatos comunes para números
representados en coma flotante.
Ejemplo: Escribir en formato de coma flotante los
números: a) 11011101,11012
b) 0,00001110101012
Solución (a): Se debe llevar a la forma
![]() ; primero hay que
; primero hay que
hallar la mantisa con la Ec.1.7 y luego el exponente E con
exceso;
M=+(0,1101110111010)2
E=+810=+(1000)2; si
el bit de signo es positivo entonces E'=01002.
En este caso hay que sumarle al exponente un exceso de
1610; E=
010002+100002 =
110002
La solución final queda de la siguiente
forma:
bs | Exponente E | Mantisa M |
0 | 11000 | 1101110111010 |
Solución (b): Se debe llevar a la forma
![]() ; primero hay que
; primero hay que
hallar la mantisa con la Ec.1.7 y luego el exponente E con
exceso;
M=+(0,111010101)2
E=-410=-(100)2; si
el bit de signo es negativo entonces E'=11002.
En este caso hay que sumarle al exponente un exceso de
810; E=
11002+10002 =
01002
La solución final queda de la siguiente
forma:
bs | Exponente E | Mantisa M |
0 | 0100 | 111010101 |
CÓDIGOS DE
NUMERACIÓN, ALFANUMÉRICOS Y DE
ERRORES.
Los códigos en los sistemas
digitales se clasifican en tres tipos: códigos
numéricos, códigos alfanuméricos y
códigos detectores y correctores de errores. El objetivo de
los códigos es simplificar la
comunicación entre los distintos circuitos
digitales, normalizar el funcionamiento de los mismos y detectar
posibles fallas de datos para su posterior
corrección.
1.5.1 Códigos numéricos.
Los más utilizados, en circuitos digitales
combinacionales son el código BCD, Exceso 3, Aiken o 2421,
5421, Biquinario, Dos de Cinco. Existen otros códigos de
tipo secuencial cíclicos, dos de ellos es son
código Jhonson y el código Gray. En la tabla 1.6 se
describen algunos de ellos con sus respectivos equivalentes
decimales.
Decimal | BCD | Exceso 3 | 2421 | 5421 | Biquinario | Dos de | Gray |
0 | 0000 | 0011 | 0000 | 0000 | 0100001 | 00011 | 0000 |
1 | 0001 | 0100 | 0001 | 0001 | 0100010 | 00101 | 0001 |
2 | 0010 | 0101 | 0010 | 0010 | 0100100 | 01001 | 0011 |
3 | 0011 | 0110 | 0011 | 0011 | 0101000 | 10001 | 0010 |
4 | 0100 | 0111 | 0100 | 0100 | 0110000 | 00110 | 0110 |
5 | 0101 | 1000 | 1011 | 1000 | 1000001 | 01010 | 0111 |
6 | 0110 | 1001 | 1100 | 1001 | 1000010 | 10010 | 0101 |
7 | 0111 | 1010 | 1101 | 1010 | 1000100 | 01100 | 0100 |
8 | 1000 | 1011 | 1110 | 1011 | 1001000 | 10100 | 1100 |
9 | 1001 | 1100 | 1111 | 1100 | 1010000 | 11000 | 1101 |
10 | 0001 0000 | 0100 0011 | 0001 0000 | 0001 0000 | 0100010 0100001 | 00101 00011 | 1111 |
11 | 0001 0001 | 0100 0100 | 0001 0001 | 0001 0001 | 0100010 0100010 | 00101 00101 | 1110 |
12 | 0001 0010 | 0100 0101 | 0001 0010 | 0001 0010 | 0100010 0100100 | 00101 01001 | 1010 |
13 | 0001 0011 | 0100 0110 | 0001 0011 | 0001 0011 | 0100010 0101000 | 00101 10001 | 1011 |
14 | 0001 0100 | 0100 0111 | 0001 0100 | 0001 0100 | 0100010 0110000 | 00101 00110 | 1001 |
15 | 0001 0101 | 0100 1000 | 0001 1011 | 0001 1000 | 0100010 1000001 | 00101 01010 | 1000 |
Tabla 1.6. Equivalencia desde cero hasta quince de
algunos códigos numéricos más
utilizados.
Código BCD.
(Binario Codificado en Decimal): La
conversión con el sistema decimal se realiza directamente,
en grupos de cuatro
bits por cada dígito decimal con ponderación 8421.
Este código tiene aplicación en visualizadores
(displays) hechos con diodos led o LCD,
los cuales poseen previamente convertidores que transforman el
grupo de
cuatro bits BCD en otro especial, llamado 7 segmentos.
Por ejemplo, para transformar el número decimal
7890510 en código BCD se toman los
equivalentes en grupos de cuatro bits cada uno; ver tabla
1.6:
7 | 8 | 9 | 0 | 510 | |
0111 | 1000 | 1001 | 0000 | 0101BCD | Resp: 7890510 = 0111 1000 1001 |
Para realizar la equivalencia del BCD con el sistema
binario se debe tomar la precaución de realizar
primero la transformación decimal y posteriormente la
conversión al BCD.
Ejemplo: Transformar en BCD los siguientes
números:
a) 10111011111112; b)
5F3C,B16
Solución (a):
10111011111112 = 601510 =
0110 0000 0001 0101BCD
Solución (b): 5F3C,B16 =
24380,687510 = 0010 0100 0011 1000 0000, 0110
1000 0111 0101BCD
SUMA EN BCD.
La suma en BCD puede dar como resultado un número
no perteneciente al código. Por ejemplo, al sumar los
números BCD 1000 + 0001 el resultado es 1001, este
número también pertenece al código; sin
embargo, cuando se suman 0111 +1000 el resultado es 1111, este
número no pertenece al código BCD y su valor
equivalente es quince unidades.
Cuando suceden estos casos es necesario sumar un factor
de corrección que depende del rango donde se encuentre el
resultado de la suma. La tabla 1.7 muestra los valores
del factor de corrección con su respectivo rango. Para el
rango binario desde diez (10102) hasta
diecinueve (100112) el factor de
corrección es seis 01102; este factor se
duplica en forma proporcional del mismo modo que aumenta la
decena en el resultado. Por lo que se debe aplicar la
fórmula ![]()
donde n es igual al valor binario de la decena del
resultado. El factor de corrección se debe aplicar siempre
y cuando el resultado de la suma sea mayor o igual a diez. Del
mismo modo, la suma debe realizarse en binario.
Factor de Binario | Valor decimal de rango | Valor decimal de la decena | Factor de corrección Decimal |
0110 | (10 ~ 19) | 1 | 6 |
1100 | (20 ~ 29) | 2 | 12 |
10010 | (30 ~ 39) | 3 | 18 |
11000 | (40 ~ 49) | 4 | 24 |
. | . | . | . |
. | . | . | . |
. | . | . | . |
Fc = | (n0 ~ | n | Fc = nx6 |
Tabla 1.7. Factores de
corrección para la suma BCD.
Ejemplo. Dado los números p, q, r
en código BCD, sumar: a) p + q + r, b) q +
r,
c) p + q y obtener el resultado también en
BCD.
p = 1000 0110 0010 0000
1001BCD; q = 0100 1001 1001 0011
0111BCD
r = 0111 1001 1000 0110 0010 0011
1001BCD
Solución (a): Los resultados que superen
el 1001 hay que sumarle el factor de corrección
según la tabla 1.7 y llevar el acarreo
correspondiente.

Solución (b): Los resultados que superen
el 1001 hay que sumarle el factor de corrección
según la tabla 1.7 y llevar el acarreo
correspondiente.

Solución (c): Los resultados que superen
el 1001 hay que sumarle el factor de corrección
según la tabla 1.7 y llevar el acarreo
correspondiente.

CÓDIGO EXCESO 3.
Es un código igual al BCD, sin embargo se deben
añadir tres unidades a este para transformarlo en exceso
3.
CÓDIGO AIKEN O 2421.
La ponderación de este código es diferente
al BCD, para hallar su peso se debe tomar también grupos
de cuatro bits, considerando los valores 2421,
por dígito decimal.
Este código se conoce como autocomplementado a
uno porque sus diez valores, en la tabla 1.6; se pueden formar,
complementando, a partir de los primeros cinco
dígitos.
CÓDIGO 5421.
La ponderación de este código es diferente
al BCD, para hallar su peso se debe tomar también grupos
de cuatro bits, considerando los valores 5421, por dígito
decimal. Este código se forma repitiendo los cinco
primeros valores de la tabla 1.6, de modo tal, que cambia solo el
bit más significativo de cero a uno.
CÓDIGO BIQUINARIO.
Necesita siete bits para formarse; siempre hay dos bits
en nivel alto (uno) y los restantes cinco deben estar en nivel
bajo (cero). El primer bit del código, en uno, se usa para
indicar si el dígito se encuentra comprendido entre 5 y 9;
el segundo bit del código, en uno, señala que se
encuentra en el rango de 0 a 4. La desventaja de este
código es la cantidad de bits que se deben utilizar para
transmitir información, siete por cada dígito.
Sin embargo, tiene la ventaja de poder realizar
fáciles algoritmos
para el chequeo de errores de transmisión; solamente se
debe detectar que hayan dos bits, en nivel uno, por cada dato.
Uno de estos se debe encontrar entre los primeros dos bits y el
otro en los cinco restantes que forman el
dígito.
CÓDIGO DOS DE CINCO.
Este código es similar al Biquinario, pero
requiere de cinco bits para el correcto funcionamiento. Dos bits
deben estar en nivel alto y los otros tres en cero.
CÓDIGO GRAY.
Este código cíclico no posee una
relación directa con la ponderación de los
dígitos del sistema decimal. Se forma cambiando el bit
menos significativo de manera continua y consecutiva. Solamente
cambia un bit, y éste, debe ser el menos significativo; de
manera que no se repita con alguna combinación anterior.
También se puede formar obteniendo las primeras ocho
combinaciones con tres bits y luego, desde la 8va
combinación hay que repetir simétricamente los
valores, cambiando solamente el bit más significativo de
cero a uno. Por ejemplo, la 8va posición es 0100 y
a continuación viene la 9na 1100; del mismo modo,
la 7ma 0101 es simétrica con la 11va 1101.
El código Gray tiene aplicaciones en contactos de
escobillas de motores, sistemas
donde solo se necesite cambiar un bit de estado
cíclicamente.
La ventaja del código Gray radica en que la
probabilidad
de ocurrir menos errores y problemas de
transición aumenta a medida que cambian mas bits de estado
simultáneamente. El cambio consecutivo del código
BCD desde 0111 a 1000 puede producir transiciones
intermedias que originan el 1111 antes de estabilizarse en
1000. Sin embargo, el código Gray pasará
desde 0111 a 0101 cambiando solamente un bit y por
lo tanto, con menos posibilidad de cometer errores.
CÓDIGOS ALFANUMÉRICOS.
Estos códigos son interpretados por el computador
como caracteres e indistintamente pueden representar símbolos numéricos, símbolos
de control y letras.
Las computadoras se comunican mediante estos códigos y los
más utilizados son el código ASCII y el
UNICODE.
CÓDIGO ASCII.
ASCII: American Standard Code Interchange
Information. Cada caracter alfanumérico esta formado por
una cadena de siete bits. Este código representa 128
símbolos diferentes entre dígitos, letras e
instrucciones de control del computador. La tabla 1.xx muestra
los símbolos con su respectivo valor hexadecimal. Por
ejemplo, para codificar la palabra UNEXPO se procede de la
siguiente forma:
1010101 1001110 1000101 1011000 1010000
1001111
U | N | E | X | P | O |
55H | 4EH | 45H | 58H | 50H | 4FH |
Tabla 1.8. Código
ASCII.
B6B5B4 | ||||||||||||||||||
B3B2B1B0 | BIN HEX | 000 0 | 001 1 | 010 2 | 011 3 | 100 4 | 101 5 | 110 6 | 111 7 | |||||||||
0000 | 0 | NUL | DLE | SP | 0 | @ | P | ` | p | |||||||||
0001 | 1 | SOH | DC1 | ! | 1 | A | Q | a | q | |||||||||
0010 | 2 | STX | DC2 | " | 2 | B | R | b | r | |||||||||
0011 | 3 | ETX | DC3 | # | 3 | C | S | c | s | |||||||||
0100 | 4 | EOT | DC4 | $ | 4 | D | T | d | t | |||||||||
0101 | 5 | ENQ | NAK | % | 5 | E | U | e | u | |||||||||
0110 | 6 | ACK | SYN | & | 6 | F | V | f | v | |||||||||
0111 | 7 | BEL | ETB | ' | 7 | G | W | g | w | |||||||||
1000 | 8 | BS | CAN | ( | 8 | H | X | h | x | |||||||||
1001 | 9 | HT | EM | ) | 9 | I | Y | i | y | |||||||||
1010 | A | LF | SUB | * | : | J | Z | j | z | |||||||||
1011 | B | VT | ESC | + | ; | K | [ | k | { | |||||||||
1100 | C | FF | FS | , | < | L | l | | | ||||||||||
1101 | D | CR | GS | – | = | M | ] | m | } | |||||||||
1110 | E | SO | RS | . | > | N | ^ | n | ~ | |||||||||
1111 | F | SI | US | / | ? | O | _ | o | DEL | |||||||||
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |