Prueba de póker

Enviado por Herrera R.

Prueba de
póker
Prueba de póker
para independencia
Pasos para aplicar la prueba es
necesario
Bibliografía

INTRODUCCIÓN

La evolutiva y capacidad de la ciencia
informática y la gran colaboración
que promueve esta a la investigación en el campo de la Ciencia de la
Computación otorgan nuevas herramientas
para apoyar el proceso de la
toma de
decisiones para múltiples disciplinas y áreas
de diseño
y manejo de la industria. La
Simulación es una de las herramientas
más importantes y más interdisciplinarias. En pocas
palabras podemos decir, que la simulación realiza cuando
la computadora
finge ser cualquier cosa.

El usuario define la estructura del
sistema que
quiere simular. Haciendo una corrida del programa a
simular se puede deducir cual será el comportamiento
dinámico de su empresa o de la
maquina que esta diseñando. Así podemos ver los
pronósticos para la demanda y
utilidad de
nuestro producto, o
ver cuando un mecanismo pueda fallar en las condiciones adversas
del ambiente donde
funcionará.

Las aplicaciones en donde se puede aplicar la
simulación parecen no tener límites.

Actualmente se simulan desde comportamientos hasta
partes pequeñas de un mecanismo, crecimiento de
poblaciones, movimiento de
geosferas en el espacio, el desarrollo de
las epidemias, el sistema digestivo
humano, las plantas
productivas, sucursales bancarias, aplicaciones es sistemas de
información, juegos, y
hasta el por que de las cosas que nos rodean, podemos mencionar
como unos pocos ejemplos de las aplicaciones de la
simulación; la creciente importancia de la
Simulación en la Investigación
de operaciones y en sus aplicaciones industriales.

En los países desarrollados, esta es una
herramienta fundamental en los procesos de
toma de decisiones para el manejo de empresas,
así como también en la planeación
de la producción. Además. Es preciso
resaltar que con el pasar de los años, la
Simulación se ha hecho cada vez más factible para
el usuario, ya que para su utilización no se requiere que
ser un especialista en computación.

PRUEBA DE POKER.

Esta prueba examina en forma individual los
dígitos del número pseudoaleatorio generado. La
forma como esta prueba se realiza es tomando 5 dígitos a
al vez y clasificándolos como : Par, dos pares, tercia,
póker quintilla full y todos diferentes. Las
probabilidades para cada una de las manos del póker
diferentes se muestran enseguida:

Todos diferentes = 0.3024

Un par = 0.504

Dos pares = 0.108

Tercia = 0.072

Full = 0.009

Quintilla = 0.0001

Con las probabilidades anteriores y con el número
de números pseudoaleatorios generados, se puede calcular
la frecuencia esperada de cada posible resultado, la cual al
compararse con la frecuencia observada, produce el
estadístico:

Si . Entonces
los números pasan la prueba.

i Pi FO FE

Todos diferentes 0.3024 3 29(0.3024)=8.7696
(8.7696-3)2/8.7696=3.7958

Un par 0.504

Dos pares 0.108

Tercia 0.072

Full 0.009

Quintilla 0.0001

55787 dos pares

33333 Quintilla

16543 Todos diferentes

17145 Un par

51575 Tercia

44343 Full

11171 Póker

Ho: Los N. A. son independientes con Si se acepta Ho.

PRUEBA DE POKER

Hipótesis Ho: ri ~
Independiente

H1:
ri ~ Dependiente

1) Probabilidades de juego
póker con 5 cartas

P(pachuca) =
0.3024 P(un par) = 0.504

P(2 pares) =
0.1080 P(tercia) = 0.0720

P(full) =
0.0090 P(póker) = 0.0045

P(quintilla) = 0.0001

2) Cálculo
frecuencia esperada FEi (n*P)

3) Cálculo de frecuencia observada FOi

Ejem: 0.48999 representa una tercia

4) Calcular el estadístico con m = 7

5) Calcular 2 y si C es menor a este valor, se
acepta la hipótesis.

PRUEBA DE POKER PARA INDEPENDENCIA.

Esta es una prueba de independencia que se basa en la
frecuencia con que se repiten los dígitos en los
aleatorios generados, por ejemplo:

en los aleatorios: 0.345, 0.777, 0.945, 0.003,
0.478

Se pueden observar los siguientes casos:

a) Los tres dígitos son iguales (0.777)
b) Los tres son diferentes (0.478, 0.345, 0.945)
c) Existe un par de iguales (0.003)

Si se examina una muestra
independiente se espera que los dígitos que componen los
números estén repartidos al azar, de manera similar
a cuando se reparte una "mano" de Poker donde se espera que las
cartas
estén distribuidas al azar en un juego legal, por eso el
nombre de la prueba.

PASOS PARA APLICAR LA PRUEBA ES
NECESARIO:

Primero: Saber la cantidad de dígitos que
formarán los aleatorios que se desean probar.

Segundo: Clasificar los casos posibles que se pueden
formar (pares de iguales, tercias, etc.).

Tercero: Calcular las probabilidades de que en esos
números se presenten los casos que se
determinaron.

Cuarto: Generar una muestra de aleatorios con el
generador a probar y clasificar la frecuencia que presentaron los
casos en la muestra.

Quinto: Efectuar una prueba ji-cuadrada para verificar
si existe evidencia estadística para afirmar que las
frecuencias observadas son diferentes a las esperadas.
En caso contrario, no se rechazará la hipótesis de
que el generador produce aleatorios independientes.

Ejemplo: Determine si hay (o no) independencia en los
aleatorios generados para el siguiente caso (con un 5% de
significancia y aplicando la prueba de Poker).

Ejemplo para aplicar la prueba de
Poker.

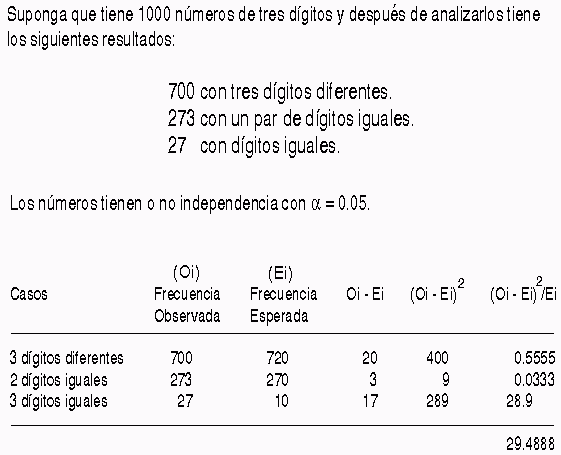
En este caso no se acepta la independencia debido a que
el valor máximo permitido (el que se lee de la tabla) fue
superado por el valor del estadístico calculado para la
muestra generada.

BIBLIOGRAFÍA

Realizado por:

Herrera R.

Cumaná

Edo. Sucre..