- Circuito en
Serie - Mixto
- Superposición de
corrientes - Leyes de
Kirchoff - Aplicación de las
leyes de Kirchoff
La conexión en paralelo se encuentra muy
frecuentemente en las casas es allí en donde se puede
entender mejor.
Pero una forma fácil de distinguirlo es
identificar que las resistencias
no se encuentren seguidas unas de otras, de esta forma si se
desconecta una de las resistencias el circuito no se
suspenderá.
Para comprender como funciona la resistencia
total, se tiene que reemplazar las resistencias por una
resistencia total pero que la batería continúe
suministrando la misma corriente que el conjunto de las
resistencias.
La
intensidad total dentro de un circuito en
paralelo se puede ver que cuando la corriente sale de la
batería y al llegar a un nudo se divide y después
se volverán a encontrar.
Por
esta razón podemos definir que la intensidad total
es:
![]()
El voltaje total (![]() ) en un circuito en paralelo se puede ver que, el
) en un circuito en paralelo se puede ver que, el
voltaje en cada resistencia será igual al Voltaje total
(![]() ) teniendo:
) teniendo:
![]()
Si varias resistencias se encuentran conectadas una de
tras de la otra se puede decir que se encuentran en
serie.
Cuando encontramos un circuito en serie se pueden
aplicar las siguientes formulas: Para la resistencia, la suma de
las resistencias es igual a la Resistencia total (B) del circuito
y esto nos lleva a:
![]()
En la Intensidad un circuito en Serie la corriente que
entra en cada resistencia es la misma que sale, y es igual a la
intensidad total de todo el circuito.
Por esto:

El circuito mixto, como su nombre lo indica combina el
circuito Simple y el paralelo teniendo de esta forma un circuito
más complejo pero más eficiente en la
práctica.
Una buena forma de resolver este tipo de Circuito es
buscar el más pequeño y resolver desde allí
hacia afuera.
Si en un circuito existen varias fuentes, la
determinación de la intensidades de corriente y de los
voltajes se puede establecer suprimiendo sucesivamente todas las
fuentes menos una y calculando los elementos del
circuito.
La solución total al problema se logra
superponiendo las soluciones
particulares tanto en magnitud como en signo.
Estas leyes son dos
reglas que permiten establecer las características de
circuitos
eléctricos de una manera sistemática y
sencilla.
Estas se conocen como ley de los nudos y ley
de las mallas.
Aplicación
de las leyes de Kirchoff
La solución del siguiente circuito en todos los
conductores, se logra aplicando las leyes de Kirchoff de la
siguiente manera:
- Se establece el número de variables
desconocidas. En este caso, el número posible de
corrientes es tres; se requieren, entonces tres ecuaciones
con tres incógnitas. - Se elige arbitrariamente la dirección de las corrientes (figura
7-b). Al final si la dirección elegida no corresponde
con la dirección de la corriente en el circuito, la
intensidad de la corriente correspondiente tendrá
signo negativo. - Se establecen las mallas existentes)
- Se escriben las ecuaciones para cada uno de los
nudos y para cada una de las mallas. Vale la pena anotar que
la dirección de las corrientes en una resistencia
indica el paso de un potencial alto a un potencial bajo; es
decir, una diferencia de negativa.
Si se recorre la fuente del borne negativo al
positivo, se pasa de un potencial bajo a un potencial alto, en
otras palabras, se trata de una diferencia de potencial
positiva. La corriente fluye en las resistencias de los puntos
se mayor potencial a los de menos potencial.
En la tabla de abajo se muestra
cómo la diferencia de potencial entre dos puntos es
independiente de la dirección en la cual se recorre el
circuito. La línea punteada indica la dirección
en la cual se recorre el circuito.

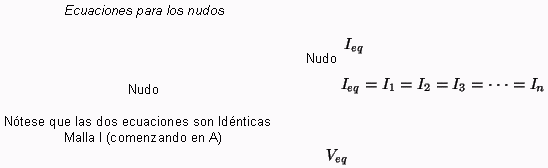
Malla II (comenzando en A)
![]()
Malla III (comenzando en A)
![]()
Nótese que la ecuación de la malla III es la suma
de las ecuaciones para las mallas I y II. En consecuencia,
poseemos tres ecuaciones para obtener las tres incógnitas
;
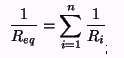
estas son las ecuaciones que encontramos
arriba.
Estas ecuaciones se solucionan de acuerdo con los
métodos
algebraicos comunes para ecuaciones simultáneas de tres
incógnitas.
La Ley de Mallas de
Kirchoff establece que la suma de todas las diferencias de
potencial a lo largo de un recorrido cerrado (malla) en el
circuito, es nula.
Es decir: Σ ΔV =
0 para un recorrido cerrado
En un circuito las cargas se mueven a través de
diferencias de potencial en las resistencias y en las
baterías.
Otra forma de establecer la Ley de Mallas es decir que,
cuando una carga realiza un recorrido cerrado y llega al punto de
salida, su energía potencial es la misma.
Las cargas positivas ganan energía cuando pasan
del polo negativo al positivo de la batería y devuelven
dicha energía cuando pasan por las resistencias.
Utilice la Ley de Mallas para determinar la corriente
suministrada por la batería en un circuito compuesto por
una batería de 16 voltios conectada a un conjunto
de tres resistencias: una de 2 ohmios en serie con una
asociación en paralelo de una resistencia de 2 y
otra de 3 ohmios
RAFAEL T.