Los gráficos
X-R se utilizan cuando la característica de calidad que se
desea controlar es una variable continua.

Para entender los gráficos X-R, es necesario conocer el
concepto de
Subgrupos (o Subgrupos racionales). Trabajar con subgrupos
significa agrupar las mediciones que se obtienen de un proceso, de
acuerdo a algún criterio. Los subgrupos se realizan
agrupando las mediciones de tal modo que haya la máxima
variabilidad entre subgrupos y la mínima variabilidad
dentro de cada subgrupo.
Por ejemplo, si hay cuatro turnos de trabajo en un
día, las mediciones de cada turno podrían
constituir un subgrupo.
Supongamos una fábrica que produce piezas
cilíndricas para la industria
automotriz. La característica de calidad que se desea
controlar es el diámetro de las piezas.
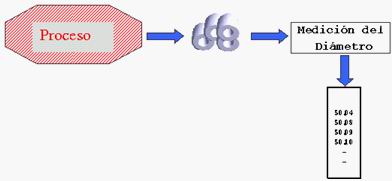
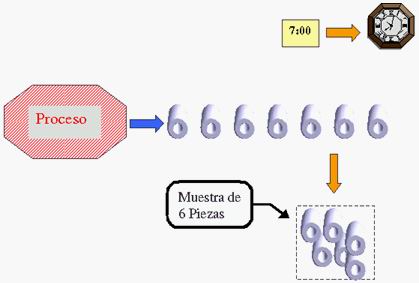
Hay dos maneras de obtener los subgrupos. Una de ellas
es retirar varias piezas juntas a intervalos regulares, por
ejemplo cada hora:
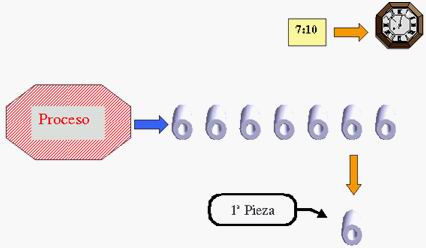
La otra forma es retirar piezas individuales a lo largo
del intervalo de tiempo
correspondiente al subgrupo:
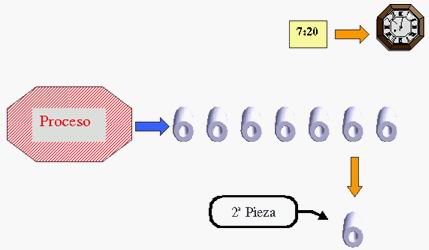
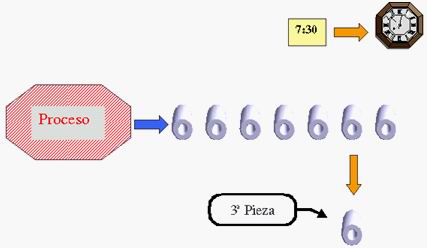
…..Etc.
Por cualquiera de los dos caminos, obtenemos grupos de igual
número de mediciones. Para cada subgrupo calculamos el
Promedio y el Rango (Diferencia entre el valor
máximo y el valor mínimo).
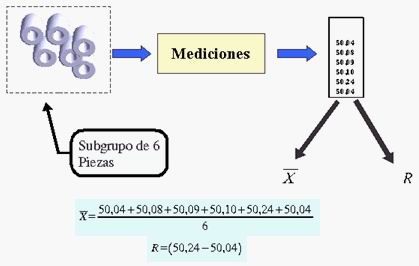
Como ya se ha visto, para calcular los
Límites
de Control es
necesario obtener un gran número de mediciones, divididas
en subgrupos. En nuestro ejemplo, podríamos obtener 30
subgrupos de 6 datos cada
uno:
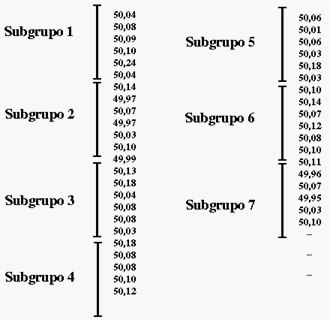
Después de calcular el Promedio y el Rango de
cada subgrupo, tendríamos una tabla como la
siguiente:
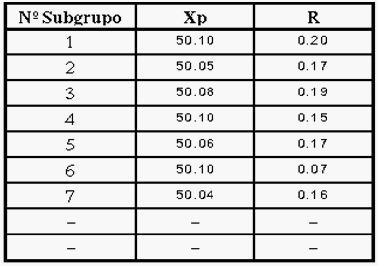
A partir de esta tabla, se calculan el promedio general
de promedios de subgrupo y el promedio de rangos de
subgrupo:

La desviación standard del proceso se puede
calcular a partir del rango promedio, utilizando el coeficiente
d2, que depende del número de mediciones en el
subgrupo:
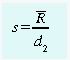
Con esto podemos calcular los Límites de Control
para el gráfico de X:

La desviación standard del rango se puede
calcular utilizando el coeficiente d3, que también depende
del número de mediciones en el subgrupo:
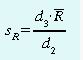
Y así podemos calcular los Límites de
Control para el Gráfico de R:

La tabla siguiente muestra los
coeficientes d2 y d3 para subgrupos de hasta 10
mediciones:
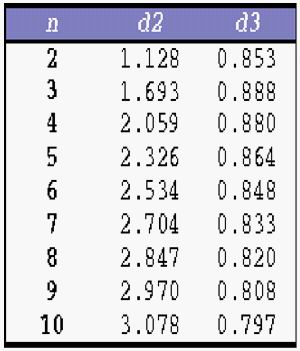
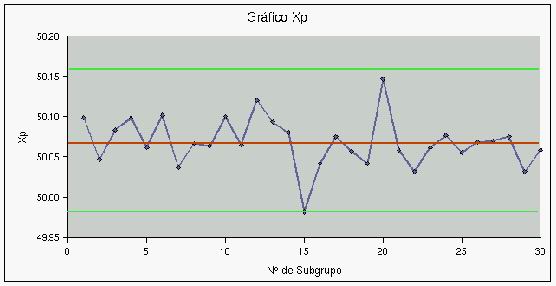
Construímos entonces un Gráfico X de
prueba y representamos los promedios de los subgrupos:
Y un Gráfico R de prueba, donde representamos los
rangos de los subgrupos:

Si no hay puntos fuera de los límites de control
y no se encuentran patrones no aleatorios, se adoptan los
límites calculados para controlar la producción futura.
Diego Armando Moreno Luis
UANE
Campus Piedras Negras
Calidad
Piedras Negras Coahuila
11 de Septiembre de 2005