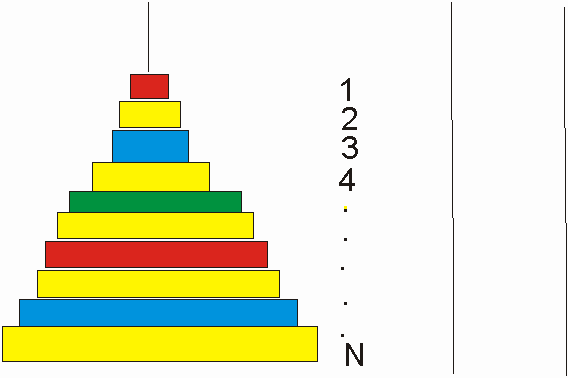Problema ( Adaptación del problema original:" Las Torres de Hanoi " )

1. Solución al
   problema
2. Ejemplo

Se tienen tres torres, en una de ellas hay n
anillos de diferentes tamaños, organizados por
tamaño, de manera que el mayor esta debajo de los
demás y así sucesivamente. El problema consiste en
mover todos los anillos a otra torre, pero con la
condición de mover solo uno cada vez, los anillos siempre
tienen que estar en una de las torres y nunca se puede colocar un
anillo mayor sobre uno menor.

SOLUCIÓN
AL PROBLEMA

Enumeremos los anillos como se muestra en la
figura.

Donde 1 es el anillo mas pequeño y
N es el anillo mas grande, es decir 1< 2< 3<
……. < N.

Sea : =
1=

=
, N,
=

Es decir: = 1=

,2, = 1,2,1

,3, =
1,2,1,3,1,2,1

.=
, N,
=

es una
sucesión de términos finitos, en la cual cada
termino es a su vez otra sucesión que depende del termino
anterior.

Los términos de la sucesión = { }, representan la
secuencia de movidas (una a la vez), que se deben hacer para
pasar los anillos de una torre a otra.

A continuación nombramos una serie de
reglas que junto con la sucesión nos
permitirá completar la solución del problema. Estas
son:

1 – El anillo , avanza a la torre siguiente.

2- Si el anillo se encuentra en la ultima torre, entonces este avanza
a la primera torre.

3- Si en la posición a la que avanzara el anillo
, se encuentra
el anillo y tal
que > j,
entonces el anillo sigue avanzando (bajo las condiciones anteriores 1 y
2).

Nota: 3 se da porque siempre se debe mantener 1
< 2 < 3……< N, y si un anillo mayor esta encima de
uno mas pequeño se daría una contradicción,
por ejemplo: 2<1 que es absurdo.

¿ Por qué se cumple lo
anterior?…

Veamos:

Por inducción matemática
tenemos lo siguiente:

=
, N,
= es cierto para N = 1, es
decir, la secuencia de movidas para cambiar N = 1 anillos a otra
torre esta dada por = 1 =, en
palabras esto es: " el anillo = 1 avanza a la torre siguiente" (por
1).

La situación se ilustra a
continuación.

Situación inicial:

 luego por = 1 =, el anillo = 1 avanza a la torre siguiente , esto es:

Para N = 2, también se cumple , esto es para mover 2 anillos de
una torre a otra la secuencia de movimientos es , veamos:

Situación inicial:

haciendo la secuencia se tiene:

1- El anillo 1 avanza a la torre siguiente:

2- El anillo 2 avanza a la torre siguiente, es decir a
la torre 2 (pero como 2 > 1, entonces 2 sigue avanzando (regla
3)):

3- el anillo 1 avanza a la torre siguiente:

Ahora, supongamos que se cumple , es decir que N anillos pueden ser movidos a otra
torre mediante la secuencia de movidas .

Ahora veamos que se cumple para k = N+1:

Supongamos que se tienen N+1 anillos:

Los primeros N anillos pueden ser movidos a otra torre
siguiendo la secuencia (pues es cierto por hipótesis de inducción)

Luego de esto el anillo N+1 puede ser puesto en otra
torre mediante un solo movimiento,
así:

Luego los N anillos, pueden ser movidos nuevamente a la
torre donde se encuentra el anillo N+1, mediante la secuencia de
movidas , pues
es cierto por
hipótesis de
inducción.

Es decir, para mover N+1 anillos de una torre a otra se
hace lo siguiente : " Se mueven los primeros N anillos mediante
la secuencia ,
se mueve el anillo N+1 a otra torre , se mueven nuevamente los N
anillos a la torre donde se encuentra el anillo N+1 mediante la
secuencia , pues
es la secuencia
para mover N anillos de una torre a otra".

Finalmente obtenemos que la secuencia para mover N+1
anillos de una torre a otra es: ,N+1, .

Pero ,N+1, =

Luego se cumple para k = N+1, Luego podemos concluir que se cumple y hemos concluido la
prueba.

Para que nos quede mas claro veamos un
ejemplo.

EJEMPLO

Se tienen tres torres, en una de ellas hay 3
anillos de diferentes tamaños, organizados por
tamaño, de manera que el mayor esta debajo de los
demás y así sucesivamente. El problema consiste en
mover todos los anillos a otra torre, pero con la
condición de mover solo uno cada vez, los anillos siempre
tienen que estar una de las torres y nunca se puede colocar un
anillo mayor sobre uno menor.

SOLUCION

Situación inicial:

Entonces hallemos :

=

Luego la secuencia de movidas es:

1. 

   

2. Movemos el anillo =1 a la torre siguiente (regla 1).

   

3. Movemos el anillo =2 a la torre siguiente (torre 2), pero como
   =2>=1 entonces el anillo =2 sigue avanzando hasta tres (regla
   3).

   

4. El anillo =1 avanza a la torre siguiente (regla 1):

   

5. El anillo = 3 avanza a la torre siguiente (regla 1):

   

6. El anillo = 1 avanza a la siguiente torre (regla 1) ,pero como el
   anillo = 1
   esta en la ultima torre, entonces este avanza a la primera
   torre (regla 2).

   

7. El anillo = 2 avanza a la torre siguiente (regla 1), es decir
   el anillo = 2
   avanza a la primera torre (regla 2), pero como 2 > 1,
   entonces este sigue avanzando hasta la segunda torre (regla
   3).
8. El anillo

= 1 avanza a la siguiente torre (regla 1)

Jorge Stibel Gallego Caro

Estudiante Escuela de
Sistemas

Universidad Nacional de Colombia – Sede
Medellín