Métodos de Formulación de Raciones (página 2)

6. Programación
lineal: raciones de mínimo costo

Las raciones o mezclas de
mínimo costo
están balanceadas con respecto a su adecuidad nutricional,
empleando las fuentes
disponibles más económicas y satisfactorias para
proporcionar los diversos nutrientes críticos en las
cantidades que se requieren.
Es importante considerar algunos aspectos que pueden determinar
la utilización de la programación lineal en producción animal.

• La alimentación
  representa entre 60 y 80% de los costos variables de
  los sistemas de
  producción animal.
• Si no alimentamos adecuadamente al animal, nunca
  podremos obtener de éste toda la producción que
  genéticamente pueda ofrecer.
• Se utiliza raciones que además de cumplir con
  el requerimiento animal, son de mínimo
  costo.
• Cuando se considera el costo de la
  alimentación, se alcanzan niveles de complejidad
  elevados donde es necesario combinar la ración
  balanceada con aquella de mínimo costo,
  recurriéndose, en este caso, a técnicas
  de optimización como la programación
  lineal.

Programación Lineal (PL) es una técnica de
optimización destinado a la asignación eficiente de
recursos
limitados en actividades conocidas para maximizar beneficios o
minimizar costos, como es el caso de la formulación de
raciones. La característica distintiva de los modelos de PL
es que las funciones que
representan el objetivo y las
restricciones son lineales.

Un programa lineal
puede ser del tipo de maximización o minimización.
Las restricciones pueden ser del tipo <=, = ó >= y
las variables pueden ser negativas o irrestrictas en signo.
Los modelos de PL a menudo representan problemas de
"asignación" en los cuales los recursos limitados se
asignan a un número de actividades.
Un Programa Lineal es un problema que se puede expresar como
sigue:
Min Z = cx (1)
Sujeto a:
Ax = b (2)
x >= 0 (3)

Donde (1) es la función
objetivo, (2) se denomina ecuaciones de
restricciones y (3) condición de no negatividad. En la
función lineal "Z=cx", "c" es el vector de precios, "x"
el vector de variables por resolver. "A" es una matriz de
coeficientes conocidos, y "b" vector de coeficientes
conocidos.
La programación lineal es utilizada en la
formulación de raciones, donde se busca minimizar el costo
de la mezcla de alimentos,
denominándose a estas, raciones de mínimo
costo.
En la ecuación (1):
Z = representa el costo de la ración a minimizar.
c = constituye el costo de cada ingrediente.
x = representan los ingredientes o alimentos en la ración
a minimizar.
En la ecuación (2):
A = es la matriz que contiene la composición nutricional
de los alimentos.
b = es el vector que representa los requerimientos nutricionales
de los animales.
En la ecuación (3):
Condición de no negatividad, indica que la cantidad a
aportar de cada alimento sea mayor o igual a cero.

Ejemplo 7
Un ejemplo de utilización de la técnica se presenta
a continuación, siendo los nutrientes aportados por los
alimentos: Energía metabolizable y Proteína cruda.
La ración será para ponedoras 7-18 semanas, los
ingredientes a utilizar son: Maíz
amarillo y Torta de soja.

El objetivo de la formulación es
determinar la cantidad de alimento X1 y X2 que debe ser mezclado
para cumplir los requerimientos de los animales y minimizar el
costo (Z) de la ración, entonces se procede a plantear el
problema de programación lineal.

Se establece la ecuación que representa la
función objetivo:
Min Z = 0.75X1 + 1.20X2 (4)
Las ecuaciones de restricciones a las cuales se sujetan la
función objetivo son:
     X1 +     X2 = 1.00
(5)
3.370X1 + 2.43X2 >= 2.85 (6)
0.088X1 + 0.44X2 >= 0.16 (7)
0.088X1 + 0.44X2 <= 0.17 (8)
X1 , X2 >= 0

Una forma de resolver problemas de programación
lineal es a través del método
gráfico. El método es eficiente para solucionar
problemas con dos restricciones para n alimentos o dos alimentos
para n restricciones. Obteniéndose así modelos
bidimensionales, si se agrega otra variable se obtiene un
modelo
tridimensional más complejo. Como el problema tiene dos
variables (X1 y X2), la solución es bidimensional.
Si se consideran las desigualdades (6, 7 y 8) en igualdades, se
tendrá:
3.370X1 + 2.43X2 = 2.85 (9)
0.088X1 + 0.44X2 = 0.16 (10)
0.088X1 + 0.44X2 = 0.17 (11)

Seguidamente se obtiene el valor de X1 y
X2 en cada una de las expresiones matemáticas. El valor de X1 y X2 en las
ecuaciones de restricción se calcula dando valor de cero a
una de ellas cuando se calcula la otra y viceversa tal como se
muestra en el
cuadro siguiente:

Con esta información es posible graficar en un eje
de coordenadas el valor de X1 y X2 de cada una de las expresiones
matemáticas, las rectas que se forman se muestran en el
gráfico siguiente:

En el polígono sombreado se muestra el
área de soluciones
factibles y cualquier combinación de los alimentos X1 y X2
que esté en el área de soluciones posibles
cumplirá con las restricciones establecidas. Por lo tanto,
el problema se limita a seleccionar la combinación de X1 y
X2 que sea de mínimo costo cumpliendo además, con
las restricciones.

Si se dan valores
arbitrarios a la función objetivo (Z) se presentan
soluciones como las que se presentan en el gráfico (Z=0.5,
Z=0.842, Z=1.0, Z=1.5). Estas rectas indican que la
función de costo de desplaza en forma paralela,
pudiéndose afirmar que si ésta se desplaza hacia
abajo, el valor de Z disminuye, mientras que un desplazamiento
hacia arriba elevará el valor de Z.
Si trazamos rectas paralelas de funciones objetivos en
el área de soluciones factibles, las posibles soluciones
se reducen a dos y corresponden a los cruces de la recta A
(ecuación 5) con la C (ec. 10) y de la recta A con la D
(ec. 11). La selección
se basa a que son los únicos vértices que cumplen
la restricción donde la suma de los alimentos es igual a
uno (X1 + X2 = 1).

Como lo que se busca es encontrar la solución que
minimice la función objetivo, la solución
óptima es aquella indicada en el gráfico.
El mencionado punto corresponde aproximadamente a 0.8 unidades de
X1 (maíz amarillo) y 0.2 unidades de X2 (Torta de soja).
Es posible calcular los valores de
estas variables resolviendo el sistema de
ecuaciones formado por el vértice de solución, que
son:
X1 + X2 = 1.00
0.088X1 + 0.44X2 = 0.16
Resolviendo este sistema se tiene:
X1 = 0.795
X2 = 0.205

Estos valores obtenidos son casi los mismos al logrado
con el gráfico. Asimismo, los resultados de las variables,
están expresadas en función a 1 kg, por tanto para
una mejor expresión se debe llevar a porcentaje, siendo el
Maíz amarillo = 79.5% y la Torta de soja = 20.5%.
La ecuación de costos es la siguiente:
Z = 0.75X1 + 1.20X2
Z = 0.75(0.795) + 1.20(0.205)
Z = S/. 0.842
La ración balanceada tiene un costo mínimo de S/.
0.842.
Comprobando si la solución satisface las igualdades y
desigualdades establecidas, se tiene:
X1 + X2 = 1.00 (5)
0.795 + 0.205 = 1.00
1.00 = 1.00
3.37X1 + 2.43X2 >= 2.85 (6)
3.37(0.795) + 2.43(0.205) = 3.18
3.18 > 2.85
0.088X1 + 0.44X2 >= 0.16 (7)
0.088(0.795) + 0.44(0.205) = 0.16
0.16 = 0.16
0.088X1 + 0.44X2 <= 0.17 (8)
0.088(0.795) + 0.44(0.205) = 0.16
0.16 < 0.17

Los modelos matemáticos formulados con la
programación lineal se pueden resolver en forma
gráfica y matemática. Para la solución
matemática, el simplex es el método empleado
comúnmente.
El método gráfico es limitado frente al simplex, su
utilización es con fines explicativos como en el anterior
ejemplo, donde se ilustra el modelo de programación lineal
en la resolución de problemas de minimización.
Obviamente, cuando deseamos formular una ración en
producción animal, utilizaremos mayores números de
ingredientes y nutrientes, cada uno con sus respectivas
restricciones, este problema es limitado para el método
gráfico, pero no para el simplex. Las operaciones
matemáticas del método
simplex son lo suficientemente complejas como para que casi
todo el modelo se efectúe mediante software.
Precisamente, el método más usado en la
confección de raciones de mínimo costo es el
método simplex, el mismo que es implementado en un
software, donde es factible especificar valores mínimos,
máximos, rangos, relaciones o cantidades exactas para cada
ingrediente o nutriente.

Ejemplo 8
El siguiente problema corresponde a una ración de
mínimo costo cuya solución se basa en el
método simplex, desarrollado a través del software
Uffda. Se emplea este programa dado su carácter
educativo y libre (ver bibliografía para una
copia).
En la utilización del software, se debe conocer aspectos
básicos que permitirán un adecuado ingreso de
datos al
programa, teniéndose las siguientes formas de expresar los
ingredientes:

A libre acceso
Cuando no se le indica ninguna restricción al ingrediente
y se desea que la computadora
utilice el nivel más conveniente en la dieta. Un ejemplo
lo es el maíz como fuente de energía y la harina de
soya como fuente de proteína. También esto ocurre
con los aminoácidos sintéticos y las fuentes de
calcio y fósforo.

Nivel exacto o fijo
Se usa cuando queremos que aparezca una cantidad fija en la
dieta. Esto sucede principalmente con las premezclas de vitaminas,
minerales
traza y aditivos no nutricionales.

Nivel mínimo
Es cuando queremos garantizar la inclusión mínima
de un ingrediente en el alimento y dejamos a la computadora la
elección de cualquier cantidad a incluir a partir de ese
nivel mínimo. Un ejemplo lo es un nivel igual o mayor que
10% de sorgo en la dieta, esto nos indica que deseamos incluir
como mínimo 10% de sorgo en la dieta.

Nivel máximo
Cuando indicamos a la computadora que no deseamos utilizar un
nivel mayor al determinado, por razones nutricionales o por
restricciones químicas o físicas. La computadora
escogerá el nivel óptimo entre cero y el nivel
máximo permitido. Un ejemplo lo es un nivel menor o igual
que 5% de harina de pescado

Nivel dentro de un rango
Es cuando queremos utilizar un nivel mínimo de un producto, pero
que a la vez no sobrepase un valor máximo. Este concepto se
aplica con la utilización de grasas y aceites en climas
calientes. Un ejemplo lo es poner un valor mínimo de 2% y
un máximo de 6%, de aceite, ya que niveles superiores
afectan la manufactura y
el almacenamiento
del producto.
Cuando expresamos los alimentos en las cuatro últimas
formas, se entiende por Límites de
Ingredientes, los mismos que son debidos a factores de
disponibilidad, composición nutricional, naturaleza propia
del ingrediente (químicas y físicas), especie
animal, económicas. Este mismo criterio se aplica a los
nutrientes, con las particularidades del caso,
entendiéndose como Límites de Nutrientes. En otros
programas de
optimización de raciones se emplea el término
Restricción para referirse a Límites, este
último usado en Uffda.
La ración a balancear será aquella para broilers
0-3 semanas, cuyo requerimientos nutricionales son: 3200 kcal/kg
EM, 23% PC, 1.00% Calcio, 0.45% Fósforo disponible, 1.10%
Lisina, 0.90% Met+Cis, 0.80% Treonina y 0.20% Triptófano
(NRC, 1994).
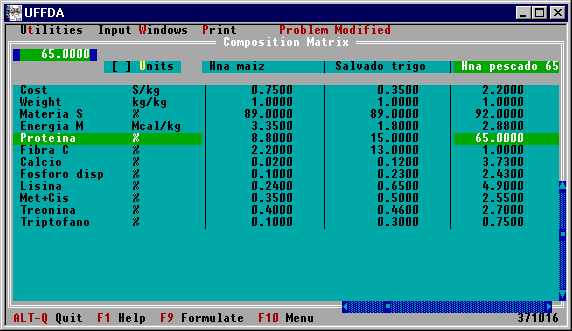
Una vez ingresado a Uffda y abrir el archivo
correspondiente, se debe acceder a la matriz de
composición de alimentos para ver la disponibilidad de los
mismos y modificar valores que crea conveniente (pantalla
inferior).

Enseguida, se ingresa los límites de
ingredientes. Para el ejemplo, se tiene un nivel mínimo de
2% de Salvado de trigo (2/100 = 0.02 en la ventana Límites
de Ingredientes), 0.20% de sal; un nivel máximo de 14% de
Harina de pescado y 4% de Aceite acidulado de pescado; niveles
exactos o fijos de 0.15% y 0.10% para Cloruro de colina y
Premezcla respectivamente. Los demás ingredientes se
ingresaron a libre acceso (pantalla inferior).

Al igual que los ingredientes, se procede con los
nutrientes, teniéndose valores exactos o fijos de 1.00 kg,
3.20 Mcal/kg y 23% PC para Weight, Energía metabolizable y
Proteína cruda respectivamente, 4.00% Fibra cruda como
nivel máximo, siendo los demás nutrientes
ingresados a un nivel mínimo (pantalla
inferior).

Finalmente, se formula la ración y puede
obtenerse un resumen en pantalla de la ración de
mínimo costo lograda; observándose que el software
excluyó a Lisina 78 por no ser necesario emplear este
alimento, dado que los alimentos logran cubrir el requerimiento
de lisina como nutriente (pantalla siguiente).

Los programas de formulación de raciones como
Uffda se presentan como una herramienta indispensable para
el aprendizaje
de formulación de raciones de mínimo costo. En el
mercado se
presentan diversos programas, la mayoría de ellos
más elaborados que el Uffda (dada su versión para
Windows), pero
los estudiantes muchas veces no están en posibilidades de
acceder a ellos por las causas que conocemos.
Sin embargo, dada las ventajas y facilidades que proporciona el
emplear software de formulación de raciones, los
resultados obtenidos deberán ser analizados
cuidadosamente, puesto que el programa se basa en una
solución al problema basado en el costo de los alimentos
sujeto a las restricciones de ingredientes y nutrientes
establecidas por el formulador. En este entender, los resultados
obtenidos podrán cumplir con las condiciones
matemáticas establecidas pero no necesariamente las
biológicas, aquellas que se observarán en la
respuesta animal.
Si las necesidades de los animales son descritas mediante modelos
determinísticos, la programación lineal es la
manera más eficaz y sencilla para la formulación de
raciones. Sin embargo, si el modelo nutricional que describe las
necesidades de los animales es estocástico (es decir que
se tiene en cuenta la variabilidad inherente de todos o varios
parámetros que participan como inputs en la
determinación de las necesidades nutricionales, entonces
la programación estocástica es necesaria para
optimizar raciones.

7.
Bibliografía

1. Alagón, H.G.; Barriga, G.J. y Salgado, M.M.
   (1996). Formulación computarizada de raciones para
   aves y
   cerdos. CIP-CIZ. Cusco, Perú.
2. Alagón, H.G.; Moscoso, M.J. y Quispe, Q.E.J.
   (2001). Formulación computarizada de raciones para aves,
   cerdos y truchas. CISPAAS-FAZ-UNSAAC. Cusco,
   Perú.
3. Campabadal, C. y Navarro, G.H.A. (1995). El papel de los
   ingredientes en la formulación de alimentos balanceados
   por computadora. C.I.N.A. – UCR – A.A.S.
4. Cañas, C.R. (1995). Alimentación y
   nutrición animal. PUC. Santiago, Chile.
5. Charaja, M. (2000). Métodos
   de optimización I. EPG-MGE-UNA. Puno,
   Perú.
6. Church, D.C. y Pond, W.G. (1992). Fundamentos de
   nutrición y alimentación de animales. Limusa.
   México.
7. Córdova A.P. (1993). Alimentación
   animal. Editec Concytec. Lima, Perú.
8. Fourier, R. (1999). Linear Programming Frequently
   Asked Questions. Optimization Technology Center of Northwestern
   University and Argonne National Laboratory. http://www-unix.mcs.anl.gov/otc/Guide/faq/linear-programming-faq.html
9. National Research Council (1988). Nutrient
   Requirements of Swine. NAP. Washington D.C.
10. National Research Council (1994). Nutrient
    Requirements of Poultry. NAP. Washington D.C.
11. Pesti, G.M., Miller, B.R. and Hargrave, J. (1992).
    User-Friendly Feed Formulation, Done Again (UFFDA). University
    of Georgia. Van Nostrand Reinhold.
    http://www.uga.edu/~poultry/progs/software.htm
12. Quispe, Q.E.J. (2001). Zootec: Formulación de
    raciones balanceadas en aves y cerdos. FAZ-UNSAAC. Cusco,
    Perú. gasunx[arroba]yahoo.com
13. Trujillo, F.V. (1987). Métodos
    matemáticos en la nutrición animal. McGraw-Hill.
    México.

Resumen
Los métodos de formulación de raciones permiten
elaborar raciones balanceadas para animales de interés
zootécnico, los hay desde los más elementales hasta
los más complejos, como la programación lineal.
Cada uno de estos métodos presenta una
característica y son destinados para raciones y
condiciones particulares, siendo elemental el aprendizaje de
estos métodos, no tanto por su aplicación en
condiciones prácticas, sino porque su ejercicio conlleva
al dominio de
técnicas y desarrollo de
habilidades al estudiante, los cuales le permitirán
elaborar con mayor facilidad raciones complejas.
Se describe los métodos Prueba y error, Ecuaciones
simultáneas, Cuadrado de Pearson y Programación
lineal, este último con desarrollo a través del
método gráfico en forma manual y a
través del método simplex mediante un software de
balanceo de raciones.
Palabras clave: Formulación de raciones,
Programación lineal, Nutrición animal,
Alimentación animal, Zootecnia.

Autor:

Elmer J. Quispe Q.

Universidad
Nacional de San Antonio Abad del Cusco
Carrera Profesional de Zootecnia