
MOTORES DE COMBUSTION INTERNA
MOTORES RECIPROCANTES
Estos motores trabajan utilizando el mecanismo cilindro pistón.
Parámetros importantes:
– Área del pistón Ap depende del diámetro del pistón Dp
– Carrera L es la distancia máxima recorrida por el pistón, representa el recorrido entre el PMS y el PMI
– Punto muerto superior (PMS): es la altura máxima a la que sube el pistón, el volumen encerrado es mínimo, llamado volumen muerto o volumen mínimo
PMS
– Punto muerto inferior (PMI): es la altura mínima a a la que baja el pistón, el volumen encerrado es máximo, llamado volumen máximo.
PMI

MOTORES DE COMBUSTION INTERNA
MOTORES RECIPROCANTES
Estos motores trabajan utilizando el mecanismo cilindro pistón.
Parámetros importantes:
– Área del pistón Ap depende del diámetro del pistón Dp
– Punto muerto superior (PMS): es la altura máxima a la que sube el pistón, el volumen encerrado es mínimo, llamado volumen muerto o volumen mínimo
PMS
– Punto muerto inferior (PMI): es la altura mínima a a la que baja el pistón, el volumen encerrado es máximo, llamado volumen máximo.
PMI
L
Entre el PMS y el PMI el pistón se desplazara un volumen Vd
Vd = Volumen desplazado.
Para un cilindro Vd = Ap * L = Cilindrada
Si un motor tiene n cilindros. Cilindrada del motor = n Ap L
– Carrera L es la distancia máxima recorrida por el pistón, representa el recorrido entre el PMS y el PMI

PRESION MEDIA EFECTIVA. Pme
En un diagrama P – V de un ciclo el área encerrada repreenta el trabajo del ciclo.
– La presión media efectiva Pme es una presión constante promedio que producirá la misma cantidad de trabajo que el ciclo real operando entre el mismo vmax y Vmin
(Gp:) V
(Gp:) P
(Gp:) Vmin Vmax
Pme
– A mayor Pme para un mismo motor operando a una misma velocidad implica mayor producción de trabajo y mayor eficiencia.
Por unidad de masa
La Pme no debe disminuir mucho ya que debe ser suficiente para vencer el roce y producir trabajo.
Para un ciclo de Carnot si aumenta QL
Pme disminuye

Relación de Compresión rc
Es la relación entre el volumen máximo y el volumen mínimo
Ciclos estudiados:
Ciclo de motores de encendido por chispa.
Simplificación Ciclo Otto.
Ciclos de motores de encendido por compresión.
Simplificación Ciclo Diesel.
Combinación de los dos ciclos.
Ciclo Dual o Semidiesel

MOTORES DE ENCENDIDO POR CHISPA
Admisión(a-1) Válvula de admisión abierta ingresa la mezcla aire combustible, el pistón se mueve hasta llegar al PMI en donde tenemos el Vmax, el proceso es a P=Cte
Compresión(1-2) Con las válvulas cerradas el pistón sube hasta el PMS, comprimiendo la mezcla hasta el volumen muerto
Combustión:(2-3) Aproximadamente un poco antes del PMS, salta la chispa de la bujía y la mezcla se enciende en un proceso a V=Cte.
(Gp:) Tiempo de expansión
Expansión(3-4): El pistón se mueve hasta el PMI, la mezcla se expende hasta el volumen máximo
Expulsión(4-1): La válvula de escape se abre y se expulsan los gases en un proceso a V= Cte aproximadamente.
(Gp:) Tiempo de Barrido
Barrido(1-a): Con la válvula de escape abierta el pistón asciende hasta el PMS, expulsando el resto de los productos de combustión, en un proceso a P=Cte

Representación de los procesos en un diagrama P – v
Los procesos a-1 y 1-a se pueden eliminar ya que producen aproximadamente el mismo trabajo.
Por tanto se estudia un ciclo termodinámico Cerrado
Este es un motor de 4 tiempos.
Un ciclo es igual a dos vueltas del cigüeñal
El ciclo teórico que mas se aproxima a un motor de encendido por chispa es el ciclo Otto.
CICLO OTTO
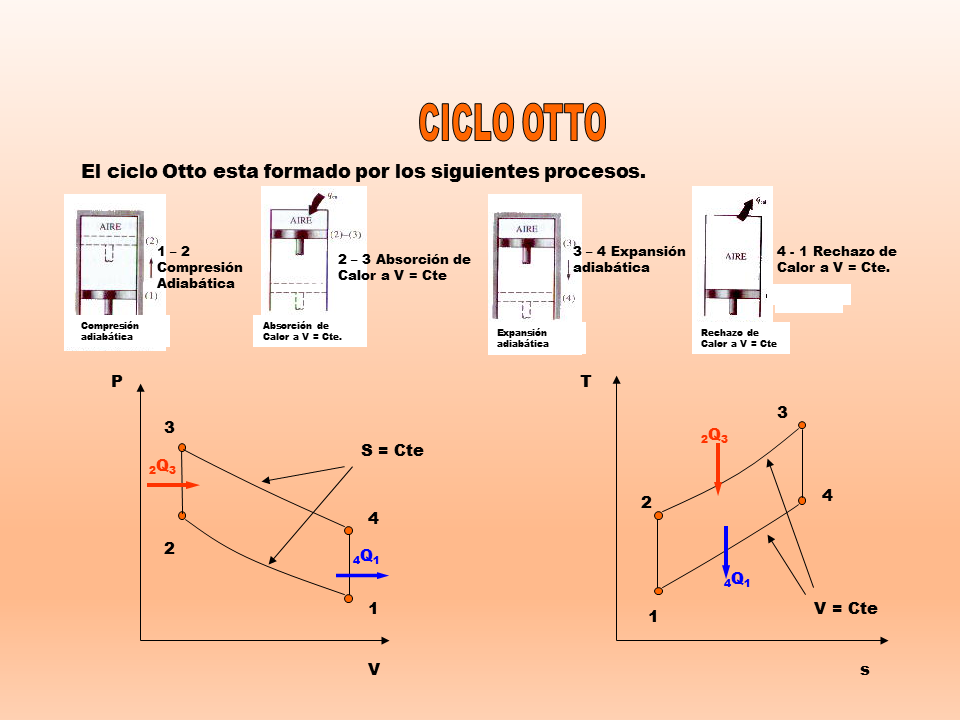
El ciclo Otto esta formado por los siguientes procesos.
1 – 2 Compresión Adiabática
2 – 3 Absorción de Calor a V = Cte
3 – 4 Expansión adiabática
4 – 1 Rechazo de Calor a V = Cte.
Expansión adiabática
4 – 1
Rechazo de Calor a V = Cte
Absorción de Calor a V = Cte.
Compresión adiabática
(Gp:) P
(Gp:) V
(Gp:) T
(Gp:) s
1
2
3
4
1
2
3
4
S = Cte
2Q3
4Q1
2Q3
4Q1
V = Cte

Calor Absorbido: 2Q3 Calor Cedido: 4Q1
Aplicando 1° Ley para Sistemas Cerrados
Proceso 2 – 3
(Gp:) 1
(Gp:) 2
(Gp:) 3
(Gp:) 4
(Gp:) 2Q3
(Gp:) 4Q1
(Gp:) V = Cte
(Gp:) T
(Gp:) s
Proceso 4 – 1

Calor Absorbido: 2Q3 Calor Cedido: 4Q1
Aplicando 1° Ley para Sistemas Cerrados
Proceso 2 – 3
(Gp:) 1
(Gp:) 2
(Gp:) 3
(Gp:) 4
(Gp:) 2Q3
(Gp:) 4Q1
(Gp:) V = Cte
(Gp:) T
(Gp:) s
Proceso 4 – 1
Dividiendo y multiplicando por T1 el numerador y por T2 el denominador

(Gp:) 1
(Gp:) 2
(Gp:) 3
(Gp:) 4
(Gp:) 2Q3
(Gp:) 4Q1
(Gp:) V = Cte
(Gp:) T
(Gp:) s
Dividiendo y multiplicando por T1 el numerador y por T2 el denominador
Analizando los procesos isentrópicos.
Proceso 1 – 2
Proceso 3 – 4

(Gp:) 1
(Gp:) 2
(Gp:) 3
(Gp:) 4
(Gp:) 2Q3
(Gp:) 4Q1
(Gp:) V = Cte
(Gp:) T
(Gp:) s
Dividiendo y multiplicando por T1 el numerador y por T2 el denominador
De los procesos 3 – 4 y 1 – 2

(Gp:) 1
(Gp:) 2
(Gp:) 3
(Gp:) 4
(Gp:) 2Q3
(Gp:) 4Q1
(Gp:) V = Cte
(Gp:) T
(Gp:) s
De los procesos 3 – 4 y 1 – 2
La eficiencia del ciclo Otto aumenta si:
Aumenta la relación de Compresión.
Si k aumenta
– La eficiencia aumenta notablemente hasta rc<8, pero luego el grado de aumento de la eficiencia se nivela.
A elevadas rc la temperatura aumenta y puede llegar a la temperatura de autoencendido. (golpeteo)
? ˜ 25 a 30%

CICLO DIESEL CON AIRE ESTANDAR
Este ciclo es una simplificación de los motores que tienen encendido por compresión.
– Se comprime solamente aire, el combustible se inyecta a presión cuando el pistón esta cerca del PMS, el resto del ciclo es similar al ciclo Otto.
– Se eleva la presión hasta que la temperatura aumente por encima de la temperatura de autoignición.
– En los motores primitivos de este tipo operaban a bajas velocidades, el proceso de combustión en el ciclo se realiza con un proceso que tiende a Presión constante
(Gp:) P
(Gp:) v
(Gp:) PMS PMI

Procesos:
1 – 2 Compresión adiabática.
2 – 3 Suministro de Calor a P = Cte.
3 – 4 Expansión adiabática.
4 – 1 Expulsión de Calor a V = Cte.
P
v
T
s

Procesos:
1 – 2 Compresión adiabática.
2 – 3 Suministro de Calor a P = Cte.
3 – 4 Expansión adiabática.
4 – 1 Expulsión de Calor a V = Cte.
P
v
T
s
1
2
3
4
1
2
3
4
2Q3
2Q3
4Q1
4Q1
P = Cte
S = Cte
V = Cte

Procesos:
1 – 2 Compresión adiabática.
2 – 3 Suministro de Calor a P = Cte.
3 – 4 Expansión adiabática.
4 – 1 Expulsión de Calor a V = Cte.
P
v
T
s
1
2
3
4
1
2
3
4
2Q3
2Q3
4Q1
4Q1
P = Cte
S = Cte
V = Cte

T
s
1
2
3
4
2Q3
4Q1
P = Cte
V = Cte
La eficiencia del ciclo Diesel viene dada por:
Proceso 1 – 4
Proceso 2 – 3
La eficiencia viene dada por:

T
s
1
2
3
4
2Q3
4Q1
P = Cte
V = Cte
La eficiencia viene dada por:
Proceso 1 – 2
Proceso 3 – 4

T
s
1
2
3
4
2Q3
4Q1
P = Cte
V = Cte
Proceso 1 – 2
Proceso 3 – 4
Proceso 2 – 3 a P = Cte.
A partir de la Ec. De gases ideales
Donde rcp = Relación de suministro de calor a P = Cte = Relación de Corte o interrupción.

A partir de la ecuación de la eficiencia.
Manipulando matemáticamente las anteriores ecuaciones e introduciendo la relación de corte y de compresión obtenemos:
La diferencia en eficiencia entre el ciclo Diesel y el Otto esta representa por la cantidad entre corchetes. El caso límite es cuando rcp = 1
La eficiencia aumenta si:
rc Aumenta y/o rcp Aumenta
Para igual rc ?otto > ?Diesel
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |