Filtros y convoluciones (Procesamiento de imágenes)

No se tiene en cuenta la relación de vecindad entre píxeles. El resultado no varía si los píxeles son permutados aleatoriamente y después reordenados.
Transformación local: el valor de un píxel depende de la vecindad local de ese píxel.
Transf. global
(Gp:) Transf. local

Entrada
Salida

Filtros y convoluciones.
Transformación global:
R(x,y):= f(A(x,y)) ó R(x,y):= f(A(x,y), B(x,y))
Filtros y transformaciones locales: R(x,y):= f(A(x-k,y-k), …, A(x,y), …, A(x+k,y+k))

Ejemplo. Filtro de la media.
R(x,y):= (A(x-1,y-1)+A(x,y-1)+A(x-1,y)+A(x,y))/4
(Gp:) ? / 4

A
R

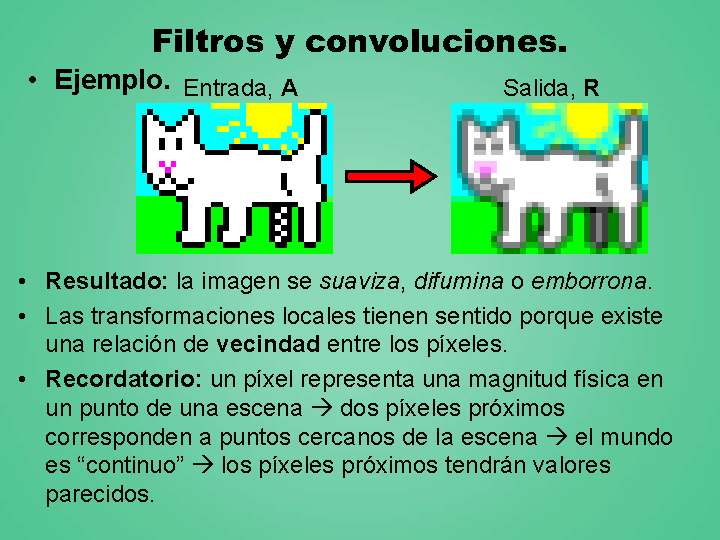
Filtros y convoluciones.
Ejemplo.
Entrada, A
Salida, R
Resultado: la imagen se suaviza, difumina o emborrona.
Las transformaciones locales tienen sentido porque existe una relación de vecindad entre los píxeles.
Recordatorio: un píxel representa una magnitud física en un punto de una escena ? dos píxeles próximos corresponden a puntos cercanos de la escena ? el mundo es “continuo” ? los píxeles próximos tendrán valores parecidos.

Filtros y convoluciones.
Un tipo interesante de transformaciones locales son las convoluciones discretas.
Convolución discreta: transformación en la que el valor del píxel resultante es una combinación lineal de los valores de los píxeles vecinos en la imagen.

Ejemplo. El filtro de la media es una convolución.
R(x,y):= 1/4·A(x-1,y-1) + 1/4·A(x,y-1) + 1/4·A(x-1,y) + 1/4·A(x,y)

Otra forma de ver la convolución:
Matriz de coeficientes de lacombinación lineal.
(x-1,y-1)
(x,y-1)
(x-1,y)
(x,y)

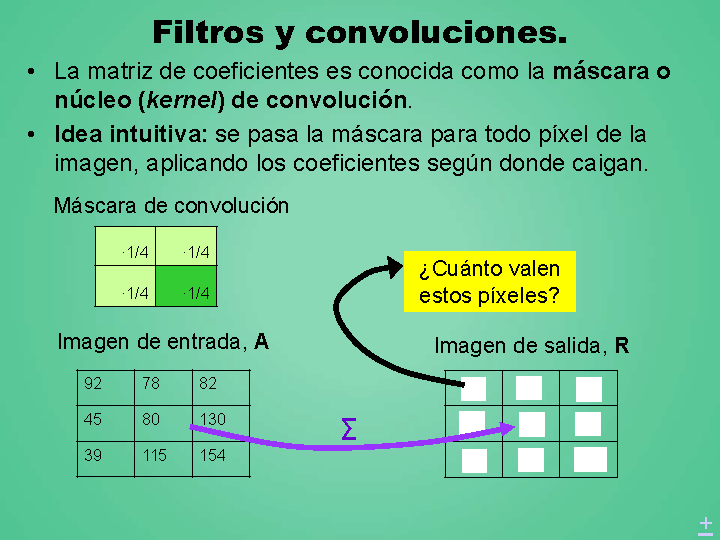
Filtros y convoluciones.
La matriz de coeficientes es conocida como la máscara o núcleo (kernel) de convolución.
Idea intuitiva: se pasa la máscara para todo píxel de la imagen, aplicando los coeficientes según donde caigan.
Máscara de convolución
Imagen de entrada, A
Imagen de salida, R
(Gp:) ?

¿Cuánto valen estos píxeles?
+

Filtros y convoluciones.
Sea M una máscara de convolución. Se puede definir como array [-k…k, -p…p] de real

Algoritmo. Cálculo de una convolución.
Denotamos la convolución como: R:= M?A
Entrada. A: imagen de maxX x maxY
M: array [-k…k, -p…p] de real
Salida. R: imagen de maxX x maxY
Algoritmo:
para cada píxel (x, y) de la imagen A hacer
R(x, y):= ? ? M(i, j)·A(x+i, y+j)
i=-k..k
j=-p..p
En X la máscara va de -k a k, y en Y de -p a p. El punto central es (0,0)

Filtros y convoluciones.
¿Cómo calcular el resultado de la combinación?
Respuesta: comprobar el efecto sobre una imagen sólo con el píxel central a UNO (“señal impulso”).
?
? 1/9·
=
? 1/9·
= 1/9·
Máscara equivalente

Filtros y convoluciones.
Resultado: el filtro de la media es separable.
En lugar de aplicar una máscara de 3×3 se pueden aplicar dos máscaras de 1×3 y 3×1 (máscaras unidimensionales).
Puede ser útil para hacer los cálculos más eficientes.
Análogamente, algunas convoluciones se pueden obtener combinando otras más simples: núcleos separables.
Ejemplo.
?A = 1/9·
1/3·
? 1/3·
?A

Filtros y convoluciones.
¿Qué hacer con lospíxeles de los bordes?

Posibilidades:
Asignar un 0 en el resultado a los píxeles donde no cabe la máscara.
Suponer que los píxeles que se salen tienen valor 0 (u otra constante).
Modificar la operación en los píxeles que no caben (variar el multiplicador).
Suponer que la imagen se extiende por los extremos (p.ej. como un espejo).
?

Filtros y convoluciones.
Las convoluciones son una discretización de la idea de convolución usada en señales. (Repasar teoría de señales…)
Diferencias: las convoluciones usadas aquí son discretas y bidimensionales.
Idea: las máscaras de convolución son matrices de números ? se pueden considerar, a su vez, como imágenes.
Propiedades:
Asociativa: M2?(M1?A) = (M2?M1)?A
Conmutativa: M2?M1?A = M1?M2?A
Ojo: al aplicar una convolución puede ocurrir saturación de píxeles. Si ocurre esto, el orden sí que puede ser importante.