Filtrado Espacial en imágenes (página 2)

Partes: 1, 2

Edge detection: gradients and derivatives
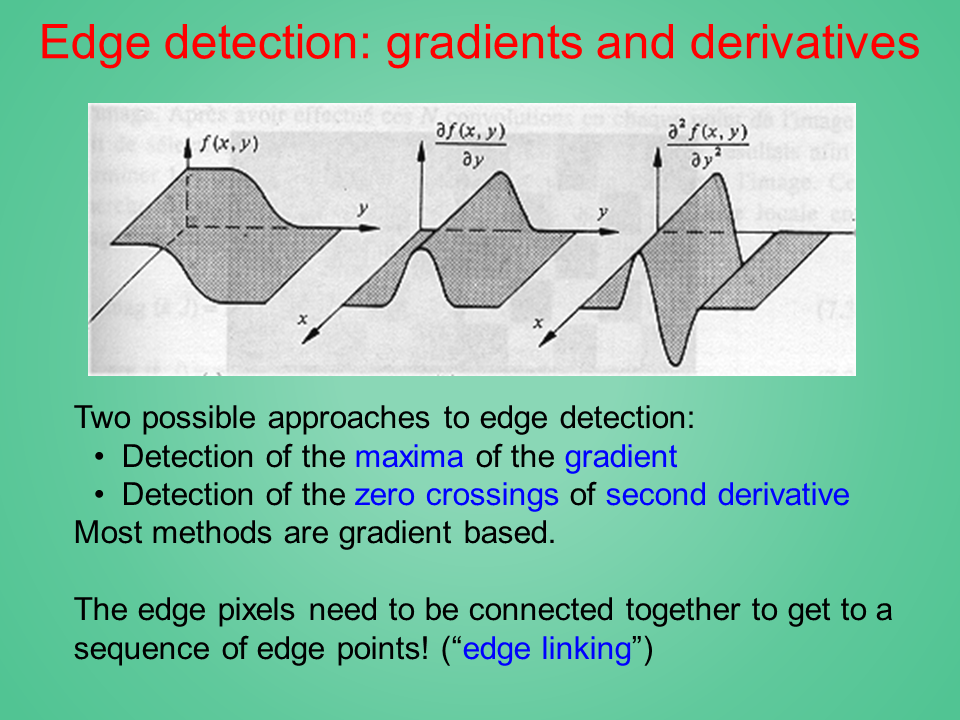
Two possible approaches to edge detection:
Detection of the maxima of the gradient
Detection of the zero crossings of second derivative
Most methods are gradient based.

The edge pixels need to be connected together to get to a sequence of edge points! (“edge linking”)

The gradient
The gradient is a vector with a norm and a direction:
The partial derivatives can be computed by convolution with appropriate linear filter masks:

Gradient: alternatives
Different possible norms:
Taking the discrete nature of an image into account:

Theorem of Taylor LaGrange applied to an image z=f(x,y)
Numerical approximation of the gradient

The Roberts filter

Differentiation with 1 pixel allows to detect fast transitions (sharp edges) but not slower transition (blurred edges)
dt
f(x)
df(x)
Problem of edge width
f(x)
df(x)

The gradient can be smoothed by averaging the pixel in the neighborhood.
Prewitt gradient filter
Increasing the differentiation step

Prewitt filter: the principal edges are better detected.
Prewitt filter: example
Roberts filter
Prewitt filter

Differentiation: noise suppression
Sobel filter

Gradient masks: summary
Roberts
Prewitt
Sobel
Mask size
A bigger mask means less sensitivity to noise
A bigger mask means higher computational complexity
A bigger mask means less localization precision

The Canny/Deriche gradient operator
In 1983 Canny proposed 3 criteria for edge detection:

Detection quality (maximum signal to noise ratio)
Localization precision
Uniqueness (one response per edge)
+ Gaussian noise
Maximization of these criteria leads to the solution of a differential equation. The solution can be approximated by the derivative of a Gaussian:

The Deriche solution
Canny’s solution has been developed for an finite impulse response filter (FIR). Deriche developed an infinite impulse response filter (IIR) from the same equations and different initial conditions:
Scale parameter
The filter is implemented as a recursive filter, i.e. the filter result of one pixel depends on the results of the preceding pixel.

?=1
?=0.5
?=0.25
Original image
?=5
?=2
A higher value of ? means a higher sensitivity to detail

Zero-Crossings (the Laplacian filter)
Instead of the maxima of the gradient we search the zero crossings of the second derivative.
The laplacian operator
Usually, the image smoothed (e.g. with a Gaussian filter) before calculating the derivative. Using the properties of convolution, this can be done in one step:
The “mexican hat” filter:

The Laplacian filter: properties
Advantages:
Closer to mechanisms of visual perception (ON/OFF cells)
One parameter only (size of the filter)
No threshold
Produces closed contours

Disadvantages:
Is more sensitive to noise (usage of second derivative)
No information on the orientation of the contour

Combination of gradient and contour
Search of zero-crossings of the Laplacian in the neighborhood of local maxima of the gradient

Laplacian filter: examples

Zero crossings: examples
?=1
?=2
?=3

Mejoramiento de la nitidez

Mejoramiento de la Nitidez – 1/2
Corresponde a la mejora de la calidad visual de una imagen

Se basa en los filtros “ unsharp masking ” o filtros de enmascaramiento de imagen borrosa

Principio :

Añadir detalles ( frecuencias altas ) a una imagen borrosa ( frecuencias bajas )
imagen mejorada = (A–1) imagen original + imagen filtrada paso-altas

A > 1

Mejoramiento de la Nitidez – 2/2
imagen mejorada = (A–1) imagen original + imagen filtrada paso-altas
Filtro Laplaciano ( filtro paso-altas )
A=1 : Filtro Laplaciano estándar
A>1 : una parte de la imagen original se añade a la paso-alta
A=2
¡ añade
ruido !

Filtro Unsharp Masking – 1/3
Se tiene una imagen borrosa ( pendiente pequeña ) = f
Se le resta con una pendiente aún más pequeña = fLPF
Lo anterior se multiplica por un factor = k ( entre 1 y 3 )
La señal de la diferencia anterior se suma a la original
(Gp:) Señal de la diferencia
(Gp:) Señal original
(Gp:) Señal con menos
Nitidez o borrosa

Filtro Unsharp Masking – 2/3
Se tiene una imagen borrosa ( pendiente pequeña ) = f
Se le resta con una pendiente aún más pequeña = fLPF
Lo anterior se multiplica por un factor = k ( entre 1 y 3 )
La señal de la diferencia anterior se suma a la original

señal con mayor resolución ( pendiente grande )

Nótese que :

con k = 1 :
= imagen mejorada

Filtro Unsharp Masking – 3/3
De lo anterior se obtiene la definición del filtro Unsharp Masking hUM(x, y) :

La forma del filtro Unsharp Masking hUM(x, y) depende de la forma del filtro paso-bajas hLPF(x, y)

Ejemplo :
si
entonces