
Contenido
Filtrado Espacial
Suavizado
Filtros basados en derivadas de la
función Gaussiana
Mejoramiento de la nitidez

Filtros Espaciales – 1/2
Modifican la contribución de ciertos rangos de frecuencia ( bajas, medianas, altas )
Se aplican directamente a la imagen ( espacio ) y no a una transformada de ella ( frecuencia )
El nivel de gris de un pixel se obtiene de los valores de sus vecinos
El filtrado se realiza por convolución de la imagen con los filtros espaciales

Filtros Espaciales – 2/2
Categorías según los rangos de frecuencia :
Filtros Paso-Bajas ( LPF ) , Smoothing Filters
Reducción de ruido
Suavizado
Pérdida de nitidez
Filtros Paso-Banda ( BPF )
Detección de patrones de ruido
Eliminan demasiado contenido de la imagen
Filtros Paso-Altas ( HPF ) , Sharpening Filters
Detección de cambios de luminosidad
Detección de patrones ( bordes y contornos )
Resaltado de detalles finos

Suavizado

Suavizado
Filtros de bloque
( máscaras = kernels )
Difuminado ( blurring )
Filtros binomiales ( orden 0 )

Filtros de Bloque – 1/4
Máscara o kernel : Matriz que representa el filtro
Al aplicar la convolución el filtrado de cada pixel coincide con la posición del valor central de la máscara ( mask )
El filtrado es función de los vecinos ( bloque ) alrededor del pixel central a filtrar
El filtrado corresponde a la suma de productos entre los valores de la máscara y los valores de los pixels para cada posición de la máscara

Filtros de Bloque – 2/4
Características de una máscara o kernel :
Sus valores se llaman coeficientes
Filtros paso-bajas o filtros paso-banda : La suma de sus coeficientes debe ser uno ( 1 )
Filtros paso-altas : La suma de sus coeficientes debe ser cero ( 0 )
Normalización

Filtros de Bloque – 3/4
Aplicación Iterativa
Convolucionar iterativamente N veces una imagen con un filtro de tamaño M corresponde a aplicar una sola convolución de un filtro de tamaño L :
L = 2 ? ( (M-1) / 2 ) ? N ) +1
2 x un filtro de tamaño 3 = 1 x un filtro de tamaño 5
3 x un filtro de tamaño 3 = 1 x un filtro de tamaño 7
(Gp:) ?
(Gp:) 2 ?

Filtros de Bloque – 4/4
Separabilidad
El filtro Gaussiano y el filtro promediador son separables
(Gp:) Ventaja : Complejidad computational para un filtro M ? N :
Implementación no separable: M ? N operaciones
Implementation separable: M + N operaciones
(Gp:) ya que
(Gp:) ya que

Filtro Promediador ( blur ) – 1/2
El filtrado corresponde a la convolución con el siguiente kernel :
F(x,y)=f?g ?

Incrementando tamaño ( blur more )
Kernel más grande = más difuminado
¡ Complejidad computacional !

Filtro Promediador ( blur ) – 2/2
Imagen con ruido suavizada con un kernel de 7?7

Filtros Paso-bajas
Se usa la función Gaussiana
Se aproxima en su forma discreta a través de los filtros binomiales de orden 0 ( N = 0 )
Los filtros binomiales se especifican para distintos tamaños o longitudes L ( x = 0, 1, … , L )
Caso continuo en 1D :

Filtro Binomial orden 0 – 1/3
Caso discreto en 1D :
Triángulo de Pascal :
x = 0, 1, … , L

Filtro Binomial orden 0 – 2/3
Propiedades – 1/2
Son separables en 2D : se aplica un filtro 1D en dirección x y después en dirección y
La convolución de un filtro de tamaño L consigo mismo produce uno de tamaño 2L :

Filtro Binomial orden 0 – 3/3
Propiedades – 2/2
En 2D se obtienen como :
Si L = 2, entonces :
Para no alterar la luminancia en la imagen, debido a la suma, se normalizan los filtros :

Filtro Paso-bajas Gaussiano ( soften )
Aproximación discreta de un filtro2D Gaussiano :
Suma ponderada, los pixels centrales son más importantes que los pixelsde los bordes

Comparación : Gaussiano vs Promedio
Imagen original Filtro promediador Filtro Gaussiano

Filtro Paso-bajas Gaussiano : Detalles

Filtro Binomial ( soften )
Imagen con ruido suavizada con un kernel de 7?7

Comparación : Binomial vs Promedio
Promediador Binomial

Filtros basados en derivadas de la función Gaussiana

Filtros de Derivadas de Gaussianas
Filtros Gaussianos
derivadas
discretización
Filtros binomiales ( orden N )
Detección de bordes
Gradientes
Filtro de Roberts
Filtro de Prewitt
Filtro de Sobel
Filtro Laplaciano
Filtro de Canny
Filtro de Deriche

Derivadas de Filtros Gaussianos – 1/4
Corresponden a filtros paso-altas
Se especializan en la detección de cambios bruscos :
Bordes
Contornos
Líneas
Primeras derivadas en 1D :
,
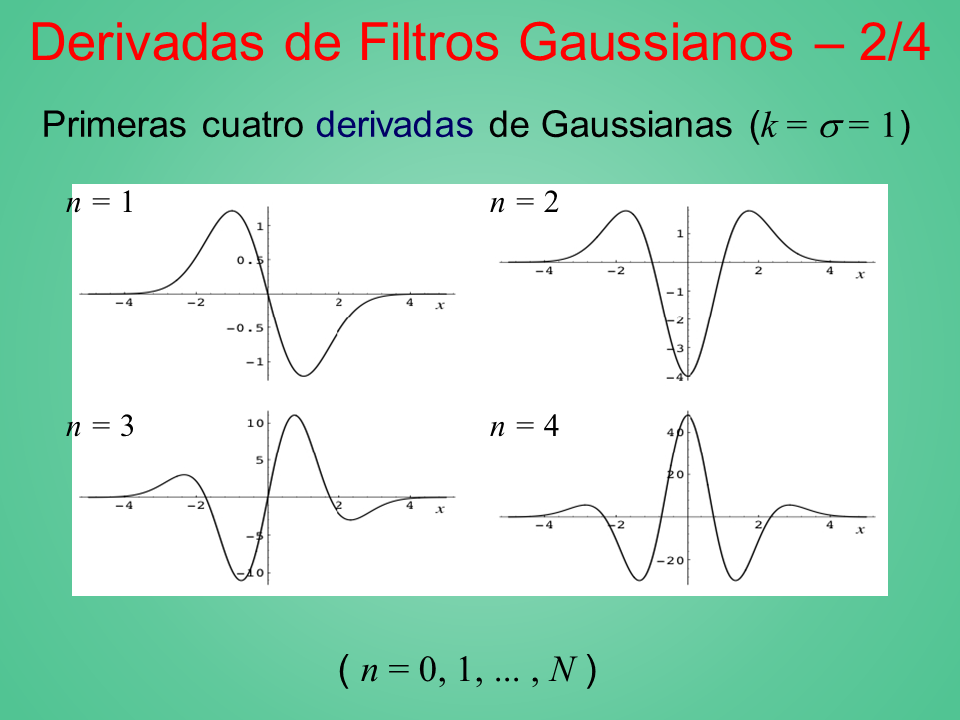
Derivadas de Filtros Gaussianos – 2/4
Primeras cuatro derivadas de Gaussianas (k = ? = 1)
( n = 0, 1, … , N )
n = 1
n = 2
n = 3
n = 4

Derivadas de Filtros Gaussianos – 3/4
Discretización de las derivadas de Gaussianas
Se define en términos de diferencias (finitas)
Forma discreta de la primera derivada Gaussiana :
Diseñando un filtro tal que y
Sabiendo que y
entonces : ó

Derivadas de Filtros Gaussianos – 4/4
Agregando un cero a h(x) :
se puede reescribir como :
h(x) posee un comportamiento discreto de la primera derivada Gaussiana

Filtro Binomial orden N
Caso discreto en 1D :
Triángulo de Pascal :
( primera derivada )
x = 0, 1, … , L
n = 0, 1, … , N

Detección de Bordes
Gradientes
Filtro de Roberts
Filtro de Prewitt
Filtro de Sobel
Filtro Laplaciano
Filtro de Canny
Filtro de Deriche
( Presentado en Inglés )
[ Tomado del curso “ Vision Industrielle ” del Dr. Carlos Rivero ]

Edges and Contours
Edges: changes in the image intensity
Página siguiente  |