
Clasificacion de los sistemas de tiempo discreto
La clasificacion de los sistemas de tiempo discreto se puede hacer de manera similar a la de los sistemas continuos:
Estaticos, dinamicos
Lineales, No lineales
Variables o invariantes en el tiempo
Causales, no causales
13

Ejemplos de sistemas de tiempo discreto
Sistema de tiempo discreto estatico
Sistema de tiempo discreto dinamico
14

Ejemplos de sistemas de tiempo discreto
Sistema de tiempo discreto variable en el tiempo
Sistema de tiempo discreto invariante en el tiempo
15

Ejemplos de sistemas de tiempo discreto
Sistema de tiempo discreto causal
Sistema de tiempo discreto no causal
16

Representacion en el dominio del tiempo de sistemas LTI de tiempo discreto
17
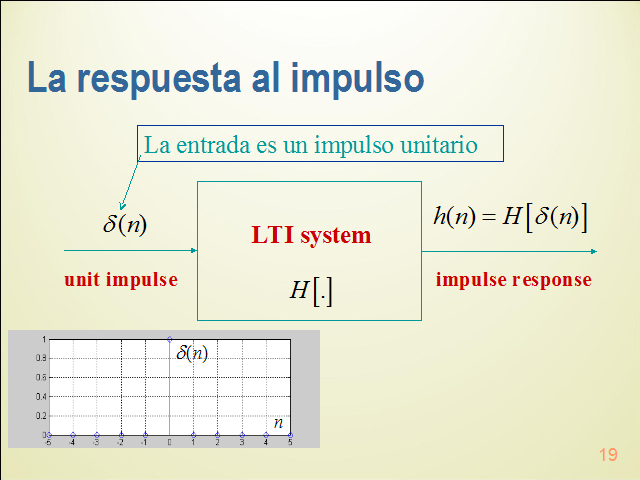
La respuesta al impulso
18
LTI system
(Gp:) unit impulse
(Gp:) impulse response
La entrada es un impulso unitario

La respuesta al impulso
La relación entre las señales de entrada y de salida se obtiene por la convolución de u con la respuesta al impulso h(t)
19
19

Respuesta al paso
20
(Gp:) unit step
(Gp:) step response
unit-step response
LTI system
Estas expresiones relacionan la respuesta al impulso y la respuesta al paso

Operadores de adelanto y de retardo
Para especificar relaciones de sistemas de tiempo discreto entre señales de entrada y salida se usan dos operadores de desplazamiento:
El operador de desplazamiento de adelanto q
El operador de desplazamiento de retardo q-1:
21

Operadores de adelanto y de retardo
El operador de desplazamiento de adelanto q
El operador de desplazamiento de retardo q-1:
22

Sistemas de tiempo discreto en terminos del operador de retardo
Siendo {h(k)} k = 0,1, ··· la respuesta al impulso del sistema,
23

Respuesta del sistema
La “funcion de transferencia” de un sistema LTI es:
24
¡no confundir con la variable compleja z!

Representacion en el dominio de la frecuencia de sistemas LTI de tiempo discreto
25
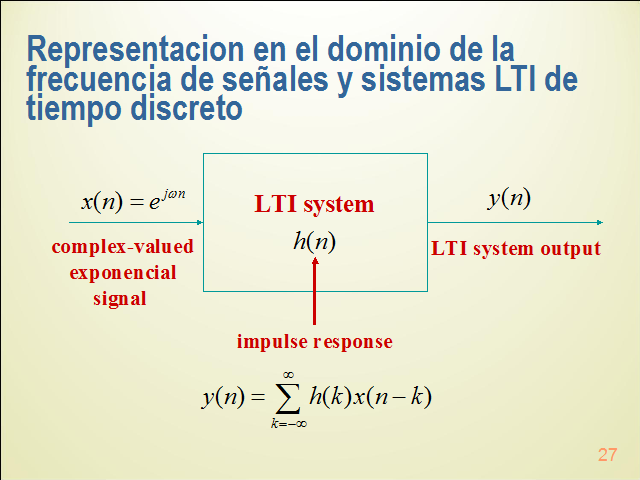
Representacion en el dominio de la frecuencia de señales y sistemas LTI de tiempo discreto
26
(Gp:) LTI system
(Gp:) complex-valued exponencial signal
(Gp:) impulse response
(Gp:) LTI system output

Representacion en el dominio de la frecuencia de señales y sistemas LTI de tiempo discreto
Calculemos la salida del sistema . . .
27

Respuesta en Frecuencia de sistemas LTI de tiempo discreto
28
Respuesta en Frecuencia

Periodicidad de la respuesta en frecuencia
Una propiedad importante de la respuesta en frecuancia es que es periodica con periodo 2p
29

30
Podemos considerar la expresion de como su expansion en series de Fourier donde h(k) son los coeficientes de la serie. En consecuencia h(k) esta relacionada con por la integral

Propiedades de simetria de la respuesta en frecuencia
La parte real es un funcion par con periodo 2p
La parte imaginaria es un funcion impar con periodo 2p
31

32
(Gp:) Symmetry Properties
(Gp:) EVEN
(Gp:) ODD

Representacion en el plano z de sistemas LTI de tiempo discreto
33

La transformada Z
Definicion: La transformada Z de una señal discreta esta definida como la serie de potencia:
34
Donde z es una variable compleja

La transformada Z inverza
El procedimiento para transformar del dominio z al dominio del tiempo es denominado la transformada Z inversa:
35
donde C denota el contorno cerrado en la region de convergencia de X(z) que contiene el origen.

La ecuacion de diferencia
Un sistema LTI de tiempo discreto puede ser descrito por medio de una ecuacion de diferencia con coeficientes constantes, como sigue
36

La funcion de transferencia
37
La aplicación de la transformada Z a la ecuacion de diferencia
Bajo la condicion de condiciones iniciales nulas
Conduce a la nocion de funcion de transferencia

La funcion de transferencia
38
(Gp:) LTI System
(Gp:) input signal
(Gp:) output signal
La Funcion de Transferencia es la razon de la transformada Z de la salida y de la transformada Z de la señal de entrada

La funcion de transferencia
La Funcion de Transferencia es la razon de la transformada Z de la salida y de la transformada Z de la señal de entrada
39

Funcion de transferencia del sistema LTI
A partir de la ecuacion de diferencia es posible calcular entonces la funcion de transferencia
40

Funcion de transferencia del sistema LTI
41
H(z): puede ser vista como una funcion racional de la variable compleja z (z-1).

Representacion en espacio de estado de sistemas LTI de tiempo discreto
42

43

Equivalencia de las representaciones
44

Equivalencia de las representaciones
45
Ejercicio
Investigue como Matlab representa un sistema dinámico de tiempo discreto en los diferentes dominios. Ver LTI_formats.m

Fuentes
Lewis Andrew, A Mathematical Introduction to Feedback Control. Queen’s University. Kingston, Canada. Abril, 2003.
Tsakalis Kostas, System properties, A Collection of Class Notes. http://www.eas.asu.edu/~tsakalis. December, 2003
Roberts Clive, Fundamentals of Signals and Systems. University of Birmingham. 2003.
Olver Peter J. and Shakiban Chehrzad, Applied Mathematics. School of Mathematics, University of Minnesota and Department of Mathematics, University of St. Thomas. 1999.
46
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |