
Title: Ejemplo 1
R = 0.500 L = 0.200 C = 0.200
a = 5.00
w0 = 25.00
wd = 24.49
Q0 = 2.50
z = 0.20
w1 = 20.50
w2 = 30.50
ancho de banda = 10.00

Title: Ejemplo 2
R = 1.000 L = 0.200 C = 0.200
a = 5.00
w0 = 25.00
wd = 24.87
Q0 = 5.00
z = 0.10
w1 = 22.62
w2 = 27.62
ancho de banda = 5.00

Title: Aproximaciones para circuitos de alta Q
Dado que
Entonces:
Y las ubicaciones de los ceros se podrían aproximar por
Un circuito de alta Q es un circuito en el cual Q0 es igual o mayor que 5

En el circuito de alta Q,
Cada frecuencia de media
Potencia se ubica aprox.
A la mitad del ancho de
Banda a partir de la frecuencia
resonante
jwd
jw2 ? j(w0 + ½?)
s2
-a
Plano s
Y(s)
jw1 ? j(w0 – ½?)
jwd ? jw0
½?
–½?

Las ubicaciones de las dos frecuencias de media potencia también se
pueden aproximar
o
La admitancia esta dada de manera aproximada por
s = jw0
s – s2
s = jw
s2
½ ?

Sustituyendo
La parte imaginaria de esta ecuación vendría siendo el numero de mitades de ancho de banda de resonancia y se abreviaría por medio de N, quedando así:
donde

La magnitud de la admitancia es
Y el ángulo estará dado por la tangente inversa
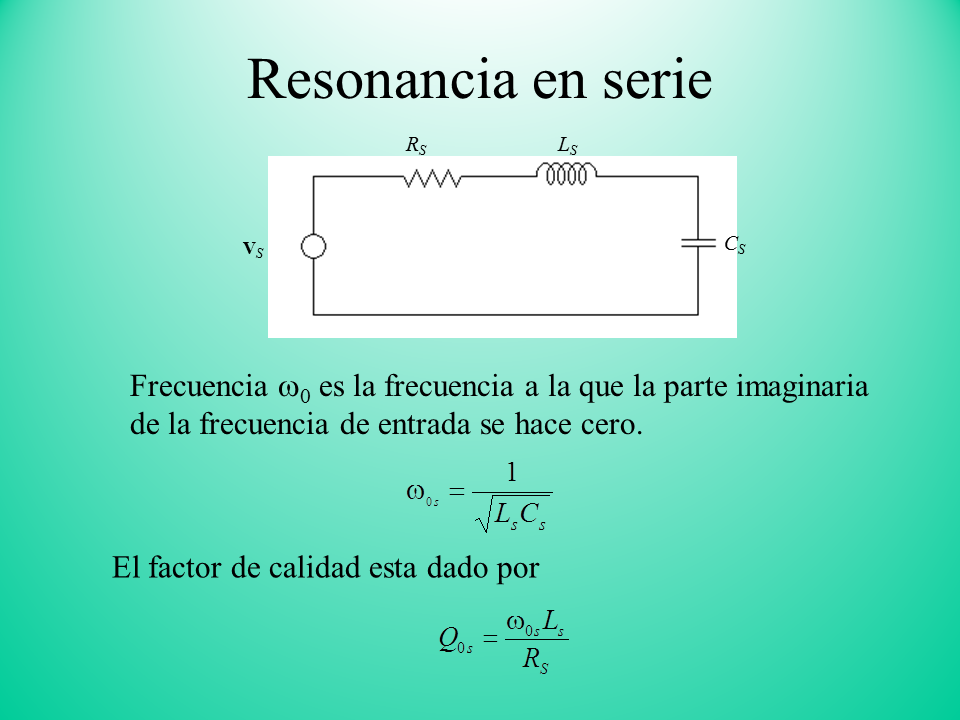
RS
VS
Frecuencia w0 es la frecuencia a la que la parte imaginaria de la frecuencia de entrada se hace cero.
Title: Resonancia en serie
CS
LS
El factor de calidad esta dado por

Las dos frecuencia w1s y w2s se definen como las frecuencias a las cuales la magnitud de la impedancia es ?2 la magnitud mínima de la impedancia.
Estas también son las frecuencias a las cuales la respuesta de corriente es igual al 70.7 % de la respuesta máxima.
Donde es la diferencia entre la frecuencia superior e inferior de la mitad de potencia .
Este ancho de banda de la mitad de potencia esta dado por
Title: Resonancia en serie

La impedancia de entrada también puede expresarse en forma aproximada para circuitos con valores altos de Qs.
Donde
El circuito resonante en serie se caracteriza por una baja impedancia resonante
Title: Resonancia en serie
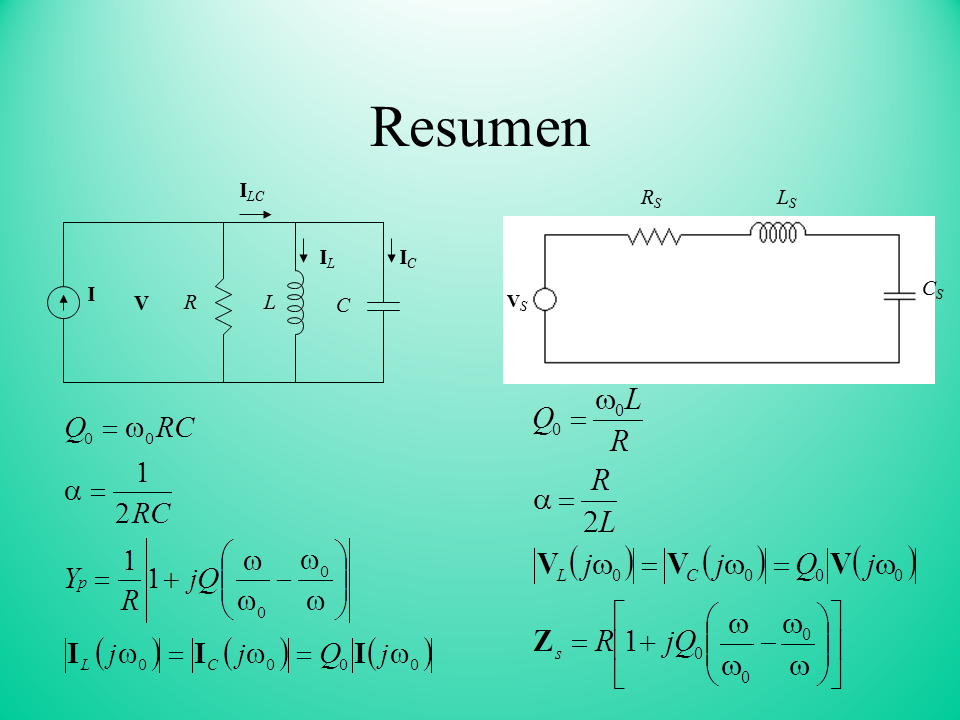
Title: Resumen
RS
VS
CS
LS
R
L
C
IL
IC
V
ILC
I

Expresiones exactas
Expresiones aproximadas
Title: Tabla de expresiones
Q0 >=5 0.9w0<= |w| <=1.1w0
wd = w0 w2, 1 = w0 ? ½ ?

Title: Tarea
Un circuito resonante serie tiene un ancho de banda de 100 Hz y contiene una inductancia de 20 mH y una capacitancia de 2 mF. Determine a) f0, b) Q0, c) Zent y d) f2.
796 Hz, 7.96, 12.57 + 0j Omhs, 846 Hz

Title: Otras formas resonantes
R1
L
C
Y
R2
Le
Ce
Re
Circuito RLC paralelo más realista y su equivalente para un rango limitado de frecuencias.

La frecuencia angular resonante se encuentra haciendo cero:
Resolviendo, obtenemos

Title: Ejemplo
Sean R1 = 2 Ohms, L = 1H, C = 1/8 F y R2 = 3 Ohms.
w0 = ?8 – 22 = 2 rad/s
Y = 1/3 + j2(1/8) + 1/(2 + j(2)(1)) = 1/3 + 1/4 = 0.583 S
Z(2j) = 1/0.583 = 1.714 Ohms
Si R1 fuera cero
w0 = 2.83 rad/s
Z(2.83j) = 1.947/_-13.26° Ohms
Frecuencia del máximo
wm = 3.26 rad/s
Z(3.26j) = 1.980/_-21.4° Ohms

Grafico de la impedancia del ejemplo
3.26máximo
2.83sin R1
w0= 2
1.714
1.947
1.980

Title: Transformación serie paralelo
El factor de calidad Q se puede definir para cualquier frecuencia, no necesariamente la de resonancia.
Puede mostrarse que para las redes serie y paralelo de las figuras el valor de Q esta dado por la expresión correspondiente.
jXs
jXp
Ys
Yp
Rs
Rp
Qs = |Xs|/Rs
Qp = Rp/|Xp|

Para que las dos redes sean equivalentes se debe cumplir lo siguiente
Esto se cumple si
Dividiendo ambas
Las Q’s de las dos redes deben ser iguales Qs = Qp = Q, por tanto

Title: Ejemplo
En w = 1000 rad/s, encuentre la red paralela equivalente a la red serie
8H
100 Ohms
Rp = 100 (1 + (8*1000)2/1002)
= 640 kOhms
Xp = 8*1000(1 + 1/ ((8*1000)2/1002))
= 8000 = 1000*Lp
Lp = 8 H

Title: Ejemplo 2
Suponga una red serie RLC con R = 20 W, L = 10 mH y C = 0.01 mF. La red es exitada por una fuente de 0.5 V y se desea medir el voltaje en el capacitor con un voltímetro con 100000 W de resistencia interna.
Antes de conectar w0 = 105 rad/s, Q0 = 50 y VC = 25 V.
El arreglo del capacitor en paralelo con la resistencia del voltímetro es equivalente a un arreglo serie de un capacitor y una resistencia.
Para calcular los valores del circuito equivalente se debe suponer que la frecuencia de resonancia es también de 105 rad/s, la Q de la red RC estará dada por
Q = Rp/|Xp| = wRC = 100
Los elementos equivalentes son
Cs = Cp y Rs = Rp/Q = 10 W
La nueva Q del circuito RLC es 33.3.
El voltaje en el arreglo serie es
|VC| = (0.5/30)|10 – j1000| = 16.67 V

Title: Tarea
Dados una resistencia de 10 W en serie con un condensador de 10 mF, determinar los dos elementos en el equivalente en paralelo si w = : a) 200, b) 1000, c) 5000 rads/s.
Resp. : 50 W, 8 mF; 1 k W, 10 mF; 25 k W, 10 mF
Para w = 105 rads/s, hallar el valor eficaz de Q para las redes RC de dos terminales que se muestran en las figuras
+—+—+ +—R2—+—+ +—+—R2—+—+ | | | | | | | R1 C R1 C R3 R1 C | | | | | | |+—+—+ +——–+—+ +—+——–+—+
R1 = 4 kW, R2 = 10 W, R3 = 500 W, C = 5mF
Resp. : 2, 10, 20

El Procedimiento de cambio de escala nos permite analizar redes formadas por elementos con valores prácticos haciendo un cambio de escala para permitir cálculos numéricos mas convenientes, tanto en magnitud como en frecuencia.
Title: Cambio de Escala

2.5 ?
½ H
2F
En el siguiente ejemplo los valores poco prácticos de sus elementos nos llevan a la improbable curva de respuesta.
Z

Title: Cambio de Escala
El cambio de escala en magnitud: se define como el proceso por medio del cual la impedancia de una red de dos terminales aumenta por un factor de Km y la frecuencia permanece constante.

Por consiguiente “la red sufrira un cambio de escala en magnitud por un factor de 2”, esto significa que la impedancia de la nueva red sera el doble de la red original:
Los siguientes cambios darán como resultado la red con otra escala en magnitud por el factor Km :
R ? Km R
L ? Km L
C ?
Cambio de escala en magnitud
Title: Cambio de Escala en Magnitud

Haciendo el cambio del circuito anterior obtenemos:
2.5 ?
½ H
2F
Z
5 k?
1000 H
10–3 F
Z

La curva de respuesta indica que, aparte de un cambio de escala en el eje vertical, no es necesario hacer ningún otro cambio en la curva de respuesta anterior.

El cambio de escala en frecuencia se define como el proceso por medio del cual la frecuencia a la que ocurre cualquier impedancia aumenta por un factor Kf
Al igual que en el caso anterior “la red sufre un cambio de escala en frecuencia por un factor de 2”.
El cambio de escala se logra cambiando la escala en frecuencia de cada elemento pasivo.
Title: Cambio de Escala en Frecuencia

Los cambios necesarios en cada elemento pasivo para hacer un cambio de escala en frecuencia por un factor Kf son:
R ? R
L ?
C ?
Cambio de escala en frecuencia
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |