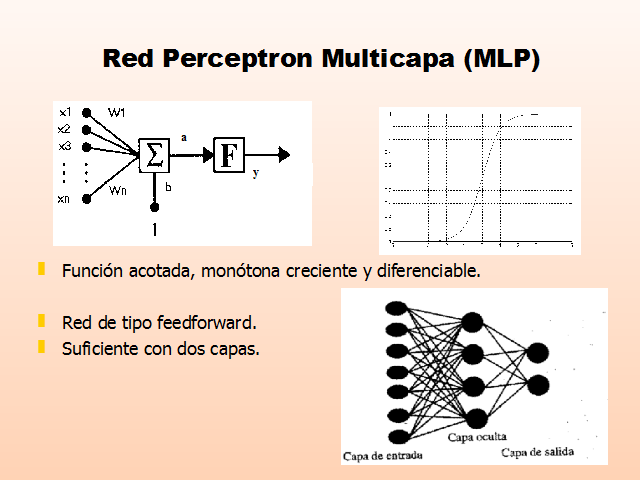
Red Perceptron Multicapa (MLP)
Función acotada, monótona creciente y diferenciable.
Red de tipo feedforward.
Suficiente con dos capas.

Algoritmo backpropagation I
Descripción:
Tras inicializar los pesos de forma aleatoria y con valores pequeños, seleccionamos el primer par de entrenamiento.
Calculamos la salida de la red
Calculamos la diferencia entre la salida real de la red y la salida deseada, con lo que obtenemos el vector de error
Ajustamos los pesos de la red de forma que se minimice el error
Repetimos los tres pasos anteriores para cada par de entrenamiento hasta que el error para todos los conjuntos de entrenamiento sea aceptable.
Descenso por la superficie del error
Cálculo de derivadas del error respecto de los pesos y de las bias.
Adelante
Atrás

Algoritmo backpropagation II
Detalles:
SSE: E=SEp=S (ypk-opk)2
Dwij=-h ?E/ ?wij
Pasos:
Inicialización:
Construcción de la red.
Inicialización aleatoria de pesos y umbrales (-0.5, 0.5)
Criterio de terminación (número máximo de iteraciones,…).
Contador de iteraciones n=0.
Fase hacia delante:
Calcular la salida de la red para cada patrón de entrada.
Calcular el error total cometido (SSE)
Si la condición de terminación se satisface, parar
Fase hacia atrás:

Algoritmo backpropagation III
Fase hacia atrás:
Incrementar el contador n=n+1.
Paca cada neurona de salida calcualr: dk=(ok-yk)f’(netk) donde netj=Siwijxi+bj
Para cada unidad oculta, calcular dj=f’(netj)Skdkwjk
Actualizar pesos: Dwij(n+1)=hdjoi+aDwij(n)
Volver a la fase hacia delante.
Inconvenientes del algoritmo backpropagation:
Tiempo de entrenamiento no acotado.
Dependiente de las condiciones iniciales:
Parálisis de la red.
Mínimos locales.

Algoritmo Backpropagation IV
Underfitting.
Memorización o Sobreaprendizaje.
Caracterización de la red. ¿Cuantas capas, cuantas neuronas en cada capa,…?

Redes Neuronales no supervisadas I
Autoorganizativas: durante el proceso de aprendizaje la red debe descubrir por si misma regularidades o categorías => la red debe autoorganizarse en función de las señales procedentes del entorno.
Mapa de Rasgos Autoorganizados, SOM (Kohonen, 80)
Características:
Red competitiva
Arquitectura unidireccional de dos capas:
Capa de entrada: m neuronas una por cada vector de entrada.
Capa segunda se realiza el procesamiento, formando el mapa de rasgos. Tiene nx X ny neuronas operando en paralelo.
Todas las neuronas de entrada están conectadas a las neuronas de la segunda capa, a través de los pesos wij

Redes Neuronales No-Supervisadas II
Cada neurona (i,j) calcula la similitud entre el vector de entradas y su vector de pesos
Vence la neurona cuyo vector de pesos es más similar al vector de entrada.
Cada neurona sirva para detectar alguna característica del vector de entrada.
Función de vecindad: relación entre neuronas próximas en el mapa.

RNA no supervisadas III
Aprendizaje:
Inicialización de los pesos wij
Presentación de las entradas x(t)
Cada neurona calcula, la similitud entre su vector de pesos wij y el vector de entrada x, usando la distancia Euclídea
Determinación de la neurona ganadora:
Actualización de los pesos de la neurona ganadora y sus vecinas
Las demás neuronas no actualizan su peso
Si se ha alcanzado el número de iteraciones parar, si no volver al paso 2.

VENTAJAS
Ventajas de las RNA:
Aprendizaje adaptativo: lo necesario es aplicar un buen algoritmo y disponer de patrones (pares) de entrenamiento.
Auto-organización => conduce a la generalización
Tolerancia a fallos: las redes pueden aprender patrones que contienen ruido, distorsión o que están incompletos.
Operación en tiempo real: procesan gran cantidad de datos en poco tiempo.
Facilidad de inserción en tecnología ya existente.

APLICACIONES
Detección de patrones.
Filtrado de señales
Segmentación de datos
Control
Identificación.

SubRedes Neuronales en identificación de sistemas

Identificación de sistemas
La identificación consiste en calcular un modelo del sistema en base a datos experimentales.
Pasos:
Seleccionar una clase de modelos (CARIMA, Box-Jenkis,…)
Obtener un conjunto de datos experimentales
Seleccionar un modelo de la clase elegida
Estimar los parámetros (método de Identificación: LS,RLS,IV,…)
Validación (exactitud, adecuación de uso)
Sistema
Entrada: u(t)
Salida: y(t)

RNA que representan el tiempo
Representación del tiempo.
Tratamiento de señales.
Identificación de modelos dinámicos
Control de sistemas.
Redes dinámicas:
Respuesta a:
Las entradas actuales
La historia pasada del sistema.
Dotar de memoria a la red:
Introduciendo directamente en la red tanto la señal actual como los valores pasados.
Mediante conexiones recurrentes.

Red PML con ventana temporal
Ventanas de datos pasadas de las entradas y de las salidas.
Ventajas:
Algoritmo simple es suficiente
No problemas de realimentación
Desventajas
Información útil debe “caber” en la ventana temporal
Muchas entradas ? Sobreparametrización
(Gp:) u(t)
(Gp:) u(t-1)
(Gp:) u(t-2)
(Gp:) …
(Gp:) u(t-m)
(Gp:) y(t-1)
(Gp:) y(t-2)
(Gp:) …
(Gp:) ym (t)
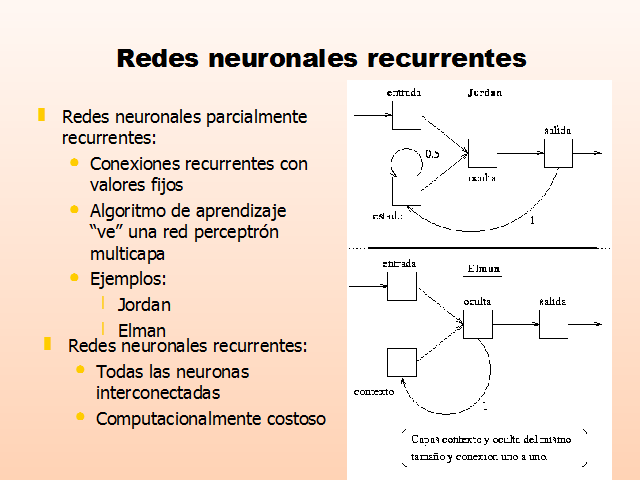
Redes neuronales recurrentes
Redes neuronales parcialmente recurrentes:
Conexiones recurrentes con valores fijos
Algoritmo de aprendizaje “ve” una red perceptrón multicapa
Ejemplos:
Jordan
Elman
Redes neuronales recurrentes:
Todas las neuronas interconectadas
Computacionalmente costoso

Estructuras neuronales para la identificación
Determinación o elección de la estructura del modelo.
¿Es necesario un modelo neuronal?
Nos basamos en modelos establecidos en el caso lineal
Diseño:
Variables que forman parte del regresor ?(t)
Función no-lineal g(·,·) desde el espacio de regresiones al espacio de salida ? NO en modelos lineales
y(t)=g(q,j(t))+e(t)
Estructura de caja negra: modelo de entrada- salida.
Elementos del regresor:
Entradas pasadas u(t-k)
Salidas pasadas medidas: y(t-k)
Salidas pasadas calculadas por el modelo: ÿu(t-k|q)
Residuos pasados calculados: eu(t-k)=y(t-k)-ÿu(t-k|q)

Modelo NARX
Ventajas:
Puede aproximar cualquier sistema no-lineal arbitrariamente bien
No recurrente.
Desventajas:
Vector de regresión puede ser grande
No se modela el ruido

Modelo NOE
Corresponde a una red recurrente, ya que parte de las entradas constituye la salida de la propia red.
Comprobación difícil para modelo de predicción estable
Entrenamiento laborioso por cálculo correcto de gradientes

Validación
Validación: es el proceso de comprobación de la utilidad de modelo obtenido:
Si el modelo concuerda con los datos observados
Si servirá al propósito para el que fue creado
Si describe el sistema real
Enfoque neuronal:
Conjunto de datos de entrenamiento
Conjunto de datos de test.
Conjunto de datos de validación.
Enfoque basado en correlaciones:
Test de blancura de los residuos
…

Ejemplo I
Transforma un producto A en otro B
Reacción química exotérmica
Se controla la temperatura mediante una camisa por la que circula un refrigerante
Salidas:
Ca Cb Tl Tr
Entradas:
Manipulables: Fl Fr
Perturbaciones medibles: Ca0 Tl0 Tr0
(Gp:) Camisa
(Gp:) Reactor
(Gp:) Fl, Ca0, Tl0
(Gp:) Fr, Tr0
(Gp:) Ca, Cb, Tl
(Gp:) Tr
(Gp:) A
(Gp:) B

Ejemplo II
El periodo de muestreo es T = 0.2 horas
Las entradas han de ser tales que provoquen todas las salidas de interés

Ejemplo III
Se normalizan los datos de entrada y salida
Se entrenan cuatro redes, cada una modela una salida
Se usa el algoritmo backpropagation
(Gp:) R.N.A. Elman
(Gp:) R.N.A. Elman
(Gp:) R.N.A. Elman
(Gp:) R.N.A. Elman
(Gp:) Ca
(Gp:) Cb
(Gp:) Tl
(Gp:) Tr
(Gp:) Fl
(Gp:) Fr
(Gp:) Ca0
(Gp:) Tl0
(Gp:) Tr0

Ejemplo IV
Validación del modelo.
De forma neuronal: test son saltos en Fr

Ejemplo V
Correlaciones: blancura de los residuos
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |